Cantor Function

In mathematics, the Cantor function is an example of a function that is continuous, but not absolutely continuous. It is a notorious counterexample in analysis, because it challenges naive intuitions about continuity, derivative, and measure. Though it is continuous everywhere and has zero derivative almost everywhere, its value still goes from 0 to 1 as its argument reaches from 0 to 1. Thus, in one sense the function seems very much like a constant one which cannot grow, and in another, it does indeed monotonically grow.

It is also called the Cantor ternary function, the Lebesgue function, Lebesgue's singular function, the Cantor–Vitali function, the Devil's staircase, the Cantor staircase function, and the Cantor–Lebesgue function. introduced the Cantor function and mentioned that Scheeffer pointed out that it was a counterexample to an extension of the fundamental theorem of calculus claimed by Harnack. The Cantor function was discussed and popularized by , and .

Definition

To define the Cantor function c: ,1to ,1/math>, let $x$ be any number in ,1/math> and obtain $c(x)$ by the following steps:

#Express $x$ in base 3.
#If the base-3 representation of $x$ contains a 1, replace every digit strictly after the first 1 by 0.
#Replace any remaining 2s with 1s.
#Interpret the result as a binary number. The result is $c(x)$.

For example:
*$\tfrac14$ has the ternary representation 0.02020202... There are no 1s so the next stage is still 0.02020202... This is rewritten as 0.01010101... This is the binary representation of $\tfrac13$, so $c(\tfrac14)=\tfrac13$.
*$\tfrac15$ has the ternary representation 0.01210121... The digits after the first 1 are replaced by 0s to produce 0.01000000... This is not rewritten since it has no 2s. This is the binary representation of $\tfrac14$, so $c(\tfrac15)=\tfrac14$.
*$\tfrac$ has the ternary representation 0.21102 (or 0.211012222...). The digits after the first 1 are replaced by 0s to produce 0.21. This is rewritten as 0.11. This is the binary representation of $\tfrac34$, so $c(\tfrac)=\tfrac34$.

Equivalently, if $\mathcal$ is the Cantor set on ,1 then the Cantor function c: ,1to ,1/math> can be defined as

:c(x) =\begin
\sum_^\infty \frac, & x = \sum_^\infty
\frac\in\mathcal\ \mathrm\ a_n\in\;
\\ \sup_ c(y), & x\in ,1setminus \mathcal.\\ \end

This formula is well-defined, since every member of the Cantor set has a ''unique'' base 3 representation that only contains the digits 0 or 2. (For some members of $\mathcal$, the ternary expansion is repeating with trailing 2's and there is an alternative non-repeating expansion ending in 1. For example, $\tfrac13$ = 0.1₃ = 0.02222...₃ is a member of the Cantor set). Since $c(0)=0$ and $c(1)=1$, and $c$ is monotonic on $\mathcal$, it is clear that $0\le c(x)\le 1$ also holds for all x\in ,1setminus\mathcal.

Properties

The Cantor function challenges naive intuitions about continuity and measure; though it is continuous everywhere and has zero derivative almost everywhere, $c(x)$ goes from 0 to 1 as uniformly continuous (precisely, it is Hölder continuous of exponent ''α'' = log 2/log 3) but not absolutely continuous. It is constant on intervals of the form (0.''x''₁''x''₂''x''₃...''x''_n022222..., 0.''x''₁''x''₂''x''₃...''x''_n200000...), and every point not in the Cantor set is in one of these intervals, so its derivative is 0 outside of the Cantor set. On the other hand, it has no derivative at any point in an uncountable subset of the Cantor set containing the interval endpoints described above.

The Cantor function can also be seen as the cumulative probability distribution function of the 1/2-1/2 Bernoulli measure ''μ'' supported on the Cantor set: c(x)=\mu( ,x. This probability distribution, called the Cantor distribution, has no discrete part. That is, the corresponding measure is atomless. This is why there are no jump discontinuities in the function; any such jump would correspond to an atom in the measure.

However, no non-constant part of the Cantor function can be represented as an integral of a probability density function; integrating any putative probability density function that is not almost everywhere zero over any interval will give positive probability to some interval to which this distribution assigns probability zero. In particular, as pointed out, the function is not the integral of its derivative even though the derivative exists almost everywhere.

The Cantor function is the standard example of a singular function.

The Cantor function is non-decreasing, and so in particular its graph defines a rectifiable curve. showed that the arc length of its graph is 2.

Lack of absolute continuity

Because the Lebesgue measure of the uncountably infinite Cantor set is 0, for any positive ''ε'' < 1 and ''δ'', there exists a finite sequence of pairwise disjoint sub-intervals with total length < ''δ'' over which the Cantor function cumulatively rises more than ''ε''.

In fact, for every ''δ'' > 0 there are finitely many pairwise disjoint intervals (''x_k'',''y_k'') (1 ≤ ''k'' ≤ ''M'') with $\sum\limits_^M (y_k-x_k)<\delta$ and $\sum\limits_^M (c(y_k)-c(x_k))=1$.

Alternative definitions

Iterative construction

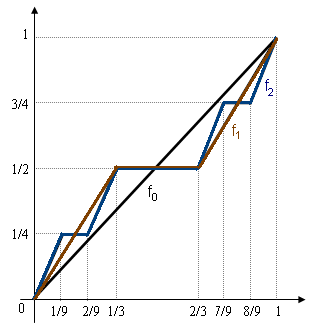Below we define a sequence of functions on the unit interval that converges to the Cantor function.

Let ''f''₀(''x'') = ''x''.

Then, for every integer , the next function ''f''_''n''+1(''x'') will be defined in terms of ''f''_''n''(''x'') as follows:

Let ''f''_''n''+1(''x'') = ,  when ;

Let ''f''_''n''+1(''x'') = 1/2,  when ;

Let ''f''_''n''+1(''x'') = ,  when .

The three definitions are compatible at the end-points 1/3 and 2/3, because ''f''_''n''(0) = 0 and ''f''_''n''(1) = 1 for every ''n'', by induction. One may check that ''f''_''n'' converges pointwise to the Cantor function defined above. Furthermore, the convergence is uniform. Indeed, separating into three cases, according to the definition of ''f''_''n''+1, one sees that

:$\max_ , f_(x) - f_n(x), \le \frac 1 2 \, \max_ , f_(x) - f_(x), , \quad n \ge 1.$

If ''f'' denotes the limit function, it follows that, for every ''n'' ≥ 0,

:$\max_ , f(x) - f_n(x), \le 2^ \, \max_ , f_1(x) - f_0(x), .$

Also the choice of starting function does not really matter, provided ''f''₀(0) = 0, ''f''₀(1) = 1 and ''f''₀ is bounded.

Fractal volume

The Cantor function is closely related to the Cantor set. The Cantor set ''C'' can be defined as the set of those numbers in the interval , 1that do not contain the digit 1 in their base-3 (triadic) expansion, except if the 1 is followed by zeros only (in which case the tail 1000$\ldots$ can be replaced by 0222$\ldots$ to get rid of any 1). It turns out that the Cantor set is a fractal with (uncountably) infinitely many points (zero-dimensional volume), but zero length (one-dimensional volume). Only the ''D''-dimensional volume $H_D$ (in the sense of a Hausdorff-measure) takes a finite value, where $D = \log(2)/\log(3)$ is the fractal dimension of ''C''. We may define the Cantor function alternatively as the ''D''-dimensional volume of sections of the Cantor set

: $f(x)=H_D(C \cap (0,x)).$

Self-similarity

The Cantor function possesses several symmetries. For $0\le x\le 1$, there is a reflection symmetry
:$c(x)=1-c(1-x)$
and a pair of magnifications, one on the left and one on the right:
:$c\left(\frac\right) = \frac$
and
:$c\left(\frac\right) = \frac$
The magnifications can be cascaded; they generate the dyadic monoid. This is exhibited by defining several helper functions. Define the reflection as
:$r(x)=1-x$
The first self-symmetry can be expressed as
:$r\circ c = c\circ r$
where the symbol $\circ$ denotes function composition. That is, $(r\circ c)(x)=r(c(x))=1-c(x)$ and likewise for the other cases. For the left and right magnifications, write the left-mappings
:$L_D(x)= \frac$ and $L_C(x)= \frac$
Then the Cantor function obeys
:$L_D \circ c = c \circ L_C$
Similarly, define the right mappings as
:$R_D(x)= \frac$ and $R_C(x)= \frac$
Then, likewise,
:$R_D \circ c = c \circ R_C$
The two sides can be mirrored one onto the other, in that
:$L_D \circ r = r\circ R_D$
and likewise,
:$L_C \circ r = r\circ R_C$
These operations can be stacked arbitrarily. Consider, for example, the sequence of left-right moves $LRLLR.$ Adding the subscripts C and D, and, for clarity, dropping the composition operator $\circ$ in all but a few places, one has:
:$L_D R_D L_D L_D R_D \circ c = c \circ L_C R_C L_C L_C R_C$
Arbitrary finite-length strings in the letters L and R correspond to the dyadic rationals, in that every dyadic rational can be written as both $y=n/2^m$ for integer ''n'' and ''m'' and as finite length of bits $y=0.b_1b_2b_3\cdots b_m$ with $b_k\in \.$ Thus, every dyadic rational is in one-to-one correspondence with some self-symmetry of the Cantor function.

Some notational rearrangements can make the above slightly easier to express. Let $g_0$ and $g_1$ stand for L and R. Function composition extends this to a monoid, in that one can write $g_=g_0g_1g_0$ and generally, $g_Ag_B=g_$ for some binary strings of digits ''A'', ''B'', where ''AB'' is just the ordinary concatenation of such strings. The dyadic monoid ''M'' is then the monoid of all such finite-length left-right moves. Writing $\gamma\in M$ as a general element of the monoid, there is a corresponding self-symmetry of the Cantor function:
:$\gamma_D\circ c= c\circ \gamma_C$

The dyadic monoid itself has several interesting properties. It can be viewed as a finite number of left-right moves down an infinite binary tree; the infinitely distant "leaves" on the tree correspond to the points on the Cantor set, and so, the monoid also represents the self-symmetries of the Cantor set. In fact, a large class of commonly occurring fractals are described by the dyadic monoid; additional examples can be found in the article on de Rham curves. Other fractals possessing self-similarity are described with other kinds of monoids. The dyadic monoid is itself a sub-monoid of the modular group $SL(2,\mathbb).$

Note that the Cantor function bears more than a passing resemblance to Minkowski's question-mark function. In particular, it obeys the exact same symmetry relations, although in an altered form.

Generalizations

Let

: $y=\sum_^\infty b_k 2^$

be the dyadic (binary) expansion of the real number 0 ≤ ''y'' ≤ 1 in terms of binary digits ''b''_''k'' ∈ . This expansion is discussed in greater detail in the article on the dyadic transformation. Then consider the function

: $C_z(y)=\sum_^\infty b_k z^.$

For ''z'' = 1/3, the inverse of the function ''x'' = 2 ''C''_1/3(''y'') is the Cantor function. That is, ''y'' = ''y''(''x'') is the Cantor function. In general, for any ''z'' < 1/2, ''C''_''z''(''y'') looks like the Cantor function turned on its side, with the width of the steps getting wider as ''z'' approaches zero.

As mentioned above, the Cantor function is also the cumulative distribution function of a measure on the Cantor set. Different Cantor functions, or Devil's Staircases, can be obtained by considering different atom-less probability measures supported on the Cantor set or other fractals. While the Cantor function has derivative 0 almost everywhere, current research focusses on the question of the size of the set of points where the upper right derivative is distinct from the lower right derivative, causing the derivative to not exist. This analysis of differentiability is usually given in terms of fractal dimension, with the Hausdorff dimension the most popular choice. This line of research was started in the 1990s by Darst, who showed that the Hausdorff dimension of the set of non-differentiability of the Cantor function is the square of the dimension of the Cantor set, $(\log2/\log3)^2$. Subsequently Falconer showed that this squaring relationship holds for all Ahlfor's regular, singular measures, i.e.$\dim_H\left\=\left(\dim_H\operatorname(\mu)\right)^2$Later, Troscheit obtain a more comprehensive picture of the set where the derivative does not exist for more general normalized Gibb's measures supported on self-conformal and self-similar sets.

Hermann Minkowski's question mark function loosely resembles the Cantor function visually, appearing as a "smoothed out" form of the latter; it can be constructed by passing from a continued fraction expansion to a binary expansion, just as the Cantor function can be constructed by passing from a ternary expansion to a binary expansion. The question mark function has the interesting property of having vanishing derivatives at all rational numbers.

See also

* Dyadic transformation

Notes

References

*
* Reprinted in: E. Zermelo (Ed.), Gesammelte Abhandlungen Mathematischen und Philosophischen Inhalts, Springer, New York, 1980.
*
*
*
*
*
*
*
*
*

External links

''Cantor ternary function'' at Encyclopaedia of Mathematics

Cantor Function
by Douglas Rivers, the Wolfram Demonstrations Project.
*

{{fractals, state=collapsed

Fractals
Measure theory
Special functions
Georg Cantor
De Rham curves