Bigoni–Piccolroaz Yield Criterion on:
[Wikipedia]
[Google]
[Amazon]
The Bigoni–Piccolroaz yield criterion is a yielding model, based on a phenomenological approach, capable of describing the mechanical behavior of a broad class of pressure-sensitive granular materials such as soil, concrete, porous metals and ceramics.
 The idea behind the Bigoni-Piccolroaz criterion is that of deriving a function capable of transitioning between the yield surfaces typical of different classes of materials only by changing the function parameters. The reason for this kind of implementation lies in the fact that the materials towards which the model is targeted undergo consistent changes during manufacturing and working conditions. The typical example is that of the hardening of a power specimen by compaction and
The idea behind the Bigoni-Piccolroaz criterion is that of deriving a function capable of transitioning between the yield surfaces typical of different classes of materials only by changing the function parameters. The reason for this kind of implementation lies in the fact that the materials towards which the model is targeted undergo consistent changes during manufacturing and working conditions. The typical example is that of the hardening of a power specimen by compaction and
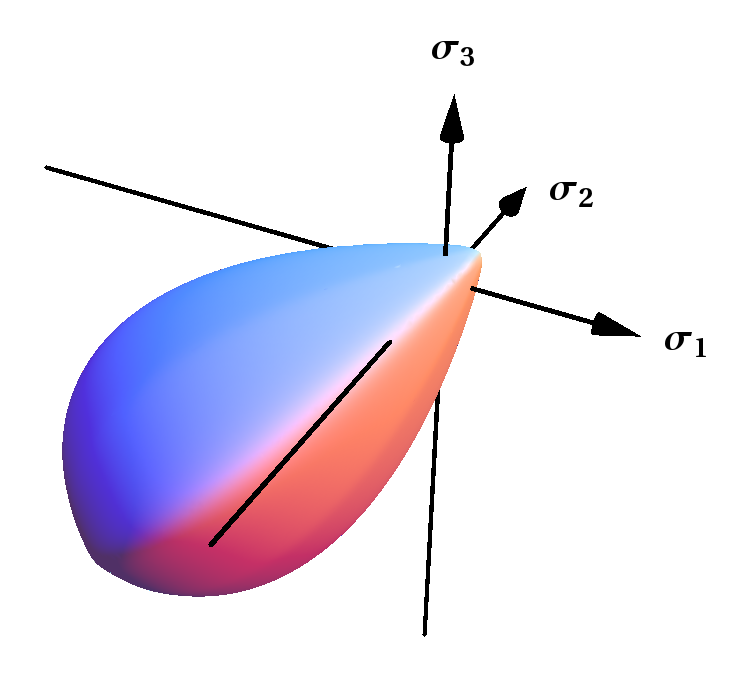 The Bigoni-Piccolroaz yield surface is thought as a direct interpolation of experimental data. This criterion represents a smooth and convex surface, which is closed both in hydrostatic tension and compression and has a drop-like shape, particularly suited to describe frictional and granular materials. This criterion has also been generalized to the case of surfaces with corners.Piccolroaz, A. and Bigoni, D. (2009), Yield criteria for quasibrittle and frictional materials: a generalization to surfaces with corners, ''International Journal of Solids and Structures'' 46, 3587–3596.
The Bigoni-Piccolroaz yield surface is thought as a direct interpolation of experimental data. This criterion represents a smooth and convex surface, which is closed both in hydrostatic tension and compression and has a drop-like shape, particularly suited to describe frictional and granular materials. This criterion has also been generalized to the case of surfaces with corners.Piccolroaz, A. and Bigoni, D. (2009), Yield criteria for quasibrittle and frictional materials: a generalization to surfaces with corners, ''International Journal of Solids and Structures'' 46, 3587–3596.


 The Bigoni–Piccolroaz yield criterion is a seven-parameter surface defined as:
:
where p, q and are invariants dependent on the stress tensor, while is the "meridian" function:
:
:
describing the pressure-sensitivity and is the "deviatoric" function:
:
describing the Lode-dependence of yielding.
The mathematical definitions of the parameters and are:
:
With:
:
Where is the deviatoric stress, is the identity tensor, is the stress tensor and the dot indicates the scalar product.
A better understanding of those important parameters can be grasped by using their geometrical representation in the Haigh–Westergaard stress space. Considering the tern of principal stresses and the deviatoric plane , orthogonal to the trisector of the first quadrant and passing through the origin of the coordinate system, the tern and unequivocally represents a point in the space acting as a cylindrical coordinate system with the trisector as an axis:
* is the distance of the point from the deviatoric plane ;
* is the distance from the trisector;
* represents the angle between the projections of and the axis on the deviatoric plane .
The usage of p and q instead of the correct cylindrical coordinates and :
:
is justified by the easier physical interpretation: p is the hydro-static pressure on the material point, q is the Von Mises equivalent stress.
The described yield function corresponds to the yield surface:
:
which makes explicit the relation between the two functions and and the shape of the meridian and deviatoric sections, respectively.
The seven, non-negative material parameters:
:
define the shape of the meridian and deviatoric sections. In particular, some of the parameters are easily relatable to mechanical properties: controls the pressure sensitivity, and are the yield strength under isotropic conditions of tension and compression. The other parameters define the shape of the surface when intersected by the meridian and deviatoric planes: and define the meridian section, and define the deviatoric section.
The Bigoni–Piccolroaz yield criterion is a seven-parameter surface defined as:
:
where p, q and are invariants dependent on the stress tensor, while is the "meridian" function:
:
:
describing the pressure-sensitivity and is the "deviatoric" function:
:
describing the Lode-dependence of yielding.
The mathematical definitions of the parameters and are:
:
With:
:
Where is the deviatoric stress, is the identity tensor, is the stress tensor and the dot indicates the scalar product.
A better understanding of those important parameters can be grasped by using their geometrical representation in the Haigh–Westergaard stress space. Considering the tern of principal stresses and the deviatoric plane , orthogonal to the trisector of the first quadrant and passing through the origin of the coordinate system, the tern and unequivocally represents a point in the space acting as a cylindrical coordinate system with the trisector as an axis:
* is the distance of the point from the deviatoric plane ;
* is the distance from the trisector;
* represents the angle between the projections of and the axis on the deviatoric plane .
The usage of p and q instead of the correct cylindrical coordinates and :
:
is justified by the easier physical interpretation: p is the hydro-static pressure on the material point, q is the Von Mises equivalent stress.
The described yield function corresponds to the yield surface:
:
which makes explicit the relation between the two functions and and the shape of the meridian and deviatoric sections, respectively.
The seven, non-negative material parameters:
:
define the shape of the meridian and deviatoric sections. In particular, some of the parameters are easily relatable to mechanical properties: controls the pressure sensitivity, and are the yield strength under isotropic conditions of tension and compression. The other parameters define the shape of the surface when intersected by the meridian and deviatoric planes: and define the meridian section, and define the deviatoric section.
General concepts
 The idea behind the Bigoni-Piccolroaz criterion is that of deriving a function capable of transitioning between the yield surfaces typical of different classes of materials only by changing the function parameters. The reason for this kind of implementation lies in the fact that the materials towards which the model is targeted undergo consistent changes during manufacturing and working conditions. The typical example is that of the hardening of a power specimen by compaction and
The idea behind the Bigoni-Piccolroaz criterion is that of deriving a function capable of transitioning between the yield surfaces typical of different classes of materials only by changing the function parameters. The reason for this kind of implementation lies in the fact that the materials towards which the model is targeted undergo consistent changes during manufacturing and working conditions. The typical example is that of the hardening of a power specimen by compaction and sintering
Sintering or frittage is the process of compacting and forming a solid mass of material by pressure or heat without melting it to the point of liquefaction. Sintering happens as part of a manufacturing process used with metals, ceramics, plas ...
during which the material changes from granular to dense.
The Bigoni-Piccolroaz yielding criterion can be represented in the Haigh–Westergaard stress space as a convex smooth surface and in fact the criterion itself is based on the mathematical definition of the surface in the above-mentioned space as a proper interpolation of experimental points.
Mathematical formulation
 The Bigoni-Piccolroaz yield surface is thought as a direct interpolation of experimental data. This criterion represents a smooth and convex surface, which is closed both in hydrostatic tension and compression and has a drop-like shape, particularly suited to describe frictional and granular materials. This criterion has also been generalized to the case of surfaces with corners.Piccolroaz, A. and Bigoni, D. (2009), Yield criteria for quasibrittle and frictional materials: a generalization to surfaces with corners, ''International Journal of Solids and Structures'' 46, 3587–3596.
The Bigoni-Piccolroaz yield surface is thought as a direct interpolation of experimental data. This criterion represents a smooth and convex surface, which is closed both in hydrostatic tension and compression and has a drop-like shape, particularly suited to describe frictional and granular materials. This criterion has also been generalized to the case of surfaces with corners.Piccolroaz, A. and Bigoni, D. (2009), Yield criteria for quasibrittle and frictional materials: a generalization to surfaces with corners, ''International Journal of Solids and Structures'' 46, 3587–3596.
Design principles
Since the whole idea of the model is to tailor a function toexperimental data
Experimental data in science and engineering is data produced by a measurement, test method, experimental design or quasi-experimental design. In clinical research any data produced are the result of a clinical trial. Experimental data may be qu ...
, the authors have defined a certain group of features as desirable, even if not essential, among those:
* smoothness of the surface;
* possibility of changing the shape and thus the interpolation on a broad class of experimental data for different materials;
* possibility to represent known criteria with limit set of parameters;
* convexity of the surface.
Parametric function


 The Bigoni–Piccolroaz yield criterion is a seven-parameter surface defined as:
:
where p, q and are invariants dependent on the stress tensor, while is the "meridian" function:
:
:
describing the pressure-sensitivity and is the "deviatoric" function:
:
describing the Lode-dependence of yielding.
The mathematical definitions of the parameters and are:
:
With:
:
Where is the deviatoric stress, is the identity tensor, is the stress tensor and the dot indicates the scalar product.
A better understanding of those important parameters can be grasped by using their geometrical representation in the Haigh–Westergaard stress space. Considering the tern of principal stresses and the deviatoric plane , orthogonal to the trisector of the first quadrant and passing through the origin of the coordinate system, the tern and unequivocally represents a point in the space acting as a cylindrical coordinate system with the trisector as an axis:
* is the distance of the point from the deviatoric plane ;
* is the distance from the trisector;
* represents the angle between the projections of and the axis on the deviatoric plane .
The usage of p and q instead of the correct cylindrical coordinates and :
:
is justified by the easier physical interpretation: p is the hydro-static pressure on the material point, q is the Von Mises equivalent stress.
The described yield function corresponds to the yield surface:
:
which makes explicit the relation between the two functions and and the shape of the meridian and deviatoric sections, respectively.
The seven, non-negative material parameters:
:
define the shape of the meridian and deviatoric sections. In particular, some of the parameters are easily relatable to mechanical properties: controls the pressure sensitivity, and are the yield strength under isotropic conditions of tension and compression. The other parameters define the shape of the surface when intersected by the meridian and deviatoric planes: and define the meridian section, and define the deviatoric section.
The Bigoni–Piccolroaz yield criterion is a seven-parameter surface defined as:
:
where p, q and are invariants dependent on the stress tensor, while is the "meridian" function:
:
:
describing the pressure-sensitivity and is the "deviatoric" function:
:
describing the Lode-dependence of yielding.
The mathematical definitions of the parameters and are:
:
With:
:
Where is the deviatoric stress, is the identity tensor, is the stress tensor and the dot indicates the scalar product.
A better understanding of those important parameters can be grasped by using their geometrical representation in the Haigh–Westergaard stress space. Considering the tern of principal stresses and the deviatoric plane , orthogonal to the trisector of the first quadrant and passing through the origin of the coordinate system, the tern and unequivocally represents a point in the space acting as a cylindrical coordinate system with the trisector as an axis:
* is the distance of the point from the deviatoric plane ;
* is the distance from the trisector;
* represents the angle between the projections of and the axis on the deviatoric plane .
The usage of p and q instead of the correct cylindrical coordinates and :
:
is justified by the easier physical interpretation: p is the hydro-static pressure on the material point, q is the Von Mises equivalent stress.
The described yield function corresponds to the yield surface:
:
which makes explicit the relation between the two functions and and the shape of the meridian and deviatoric sections, respectively.
The seven, non-negative material parameters:
:
define the shape of the meridian and deviatoric sections. In particular, some of the parameters are easily relatable to mechanical properties: controls the pressure sensitivity, and are the yield strength under isotropic conditions of tension and compression. The other parameters define the shape of the surface when intersected by the meridian and deviatoric planes: and define the meridian section, and define the deviatoric section.
Related yielding criteria
Having been designed to allow consistent changes in the surface shape in the Haigh–Westergaard stress space, the Bigoni-Piccolroazyield surface
A yield surface is a five-dimensional surface in the six-dimensional space of Stress (mechanics), stresses. The yield surface is usually convex polytope, convex and the state of stress of ''inside'' the yield surface is elastic. When the stress ...
can be used as a generalized formulation for several criteria,Bigoni, D. Nonlinear Solid Mechanics: Bifurcation Theory and Material Instability. Cambridge University Press, 2012 . . such as the well known von Mises
The Mises family or von Mises is the name of an Austrian noble family. Members of the family excelled especially in mathematics and economy.
Notable members
* Ludwig von Mises, an Austrian-American economist of the Austrian School, older bro ...
, Tresca Tresca may refer to:
* Carlo Tresca (1879–1943), Italian-born American anarchist
* Henri Tresca
Henri Édouard Tresca (12 October 1814 – 21 June 1885) was a French mechanical engineer, and a professor at the Conservatoire National des Arts et ...
, Mohr–Coulomb.
See also
*Yield surface
A yield surface is a five-dimensional surface in the six-dimensional space of Stress (mechanics), stresses. The yield surface is usually convex polytope, convex and the state of stress of ''inside'' the yield surface is elastic. When the stress ...
*Yield (engineering)
In materials science and engineering, the yield point is the point on a stress–strain curve that indicates the limit of elastic behavior and the beginning of plastic behavior. Below the yield point, a material will deform elastically and w ...
*Plasticity (physics)
In physics and materials science, plasticity (also known as plastic deformation) is the ability of a solid material to undergo permanent Deformation (engineering), deformation, a non-reversible change of shape in response to applied forces. For ...
*Material failure theory
Material failure theory is an interdisciplinary field of materials science and solid mechanics which attempts to predict the conditions under which solid materials fail under the action of external loads. The failure of a material is usually ...
*Compaction of ceramic powders
Compaction may refer to:
* Soil compaction, for mechanically induced compaction near the ground surface
* Compaction of ceramic powders
* Compaction (geology), part of the process of lithification involving mechanical dewatering of a sediment by ...
External links
The Bigoni-Piccolroaz yield surface is a powerful instrument for the characterization of granular materials and it arises great interest in the field of the definition of constitutive models for ceramics, rock and soil which is a task of fundamental importance for better design of products using these materials. * https://bigoni.dicam.unitn.it/ * https://apiccolroaz.dicam.unitn.it/ * https://www.refracture2-h2020.eu/References
{{DEFAULTSORT:Bigoni-Piccolroaz yield criterion Materials science Plasticity (physics) Yield criteria Structural analysis Ceramic materials Ceramic engineering Powders