Solid geometry or stereometry is the

geometry Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...

three-dimensional In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values (''coordinates'') are required to determine the position (geometry), position of a point (geometry), poi ...

Euclidean space Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...

(3D space). A solid figure is the

region In geography, regions, otherwise referred to as areas, zones, lands or territories, are portions of the Earth's surface that are broadly divided by physical characteristics (physical geography), human impact characteristics (human geography), and ...

of 3D space bounded by a

two-dimensional A two-dimensional space is a mathematical space with two dimensions, meaning points have two degrees of freedom: their locations can be locally described with two coordinates or they can move in two independent directions. Common two-dimension ...

closed surface In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solid figures; for example, the sphere is the boundary of the solid ball. Other surfaces ari ...

; for example, a solid

ball A ball is a round object (usually spherical, but sometimes ovoid) with several uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used for s ...

consists of a

sphere A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...

and its interior. Solid geometry deals with the

measurement Measurement is the quantification of attributes of an object or event, which can be used to compare with other objects or events. In other words, measurement is a process of determining how large or small a physical quantity is as compared to ...

s of

volume Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch) ...

s of various solids, including

pyramids A pyramid () is a Nonbuilding structure, structure whose visible surfaces are triangular in broad outline and converge toward the top, making the appearance roughly a Pyramid (geometry), pyramid in the geometric sense. The base of a pyramid ca ...

, prisms (and other polyhedrons),

cubes A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...

cylinders A cylinder () has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base. A cylinder may also be defined as an infinite ...

cones In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the ''apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, ...

(and truncated cones).

History

The

Pythagoreans Pythagoreanism originated in the 6th century BC, based on and around the teachings and beliefs held by Pythagoras and his followers, the Pythagoreans. Pythagoras established the first Pythagorean community in the Ancient Greece, ancient Greek co ...

dealt with the

regular solid In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges c ...

s, but the pyramid, prism, cone and cylinder were not studied until the

Platonist Platonism is the philosophy of Plato and philosophical systems closely derived from it, though contemporary Platonists do not necessarily accept all doctrines of Plato. Platonism has had a profound effect on Western thought. At the most fundam ...

s. Eudoxus established their measurement, proving the pyramid and cone to have one-third the volume of a prism and cylinder on the same base and of the same height. He was probably also the discoverer of a proof that the volume enclosed by a sphere is proportional to the cube of its

radius In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is th ...

.Paraphrased and taken in part from the ''

1911 Encyclopædia Britannica Events January * January 1 – A decade after federation, the Northern Territory and the Australian Capital Territory are added to the Commonwealth of Australia. * January 3 ** 1911 Kebin earthquake: An earthquake of 7.7 Mom ...

''.

Topics

Basic topics in solid geometry and stereometry include: * incidence of planes and lines * dihedral angle and

solid angle In geometry, a solid angle (symbol: ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The poin ...

* the

cube A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...

cuboid In geometry, a cuboid is a hexahedron with quadrilateral faces, meaning it is a polyhedron with six Face (geometry), faces; it has eight Vertex (geometry), vertices and twelve Edge (geometry), edges. A ''rectangular cuboid'' (sometimes also calle ...

parallelepiped In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term ''rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square. Three equiva ...

* the

tetrahedron In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...

and other

pyramid A pyramid () is a structure whose visible surfaces are triangular in broad outline and converge toward the top, making the appearance roughly a pyramid in the geometric sense. The base of a pyramid can be of any polygon shape, such as trian ...

s *

prism PRISM is a code name for a program under which the United States National Security Agency (NSA) collects internet communications from various U.S. internet companies. The program is also known by the SIGAD . PRISM collects stored internet ...

s *

octahedron In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...

dodecahedron In geometry, a dodecahedron (; ) or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three Kepler–Po ...

icosahedron In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes . The plural can be either "icosahedra" () or "icosahedrons". There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical tha ...

cone In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the '' apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines ...

s and

* the

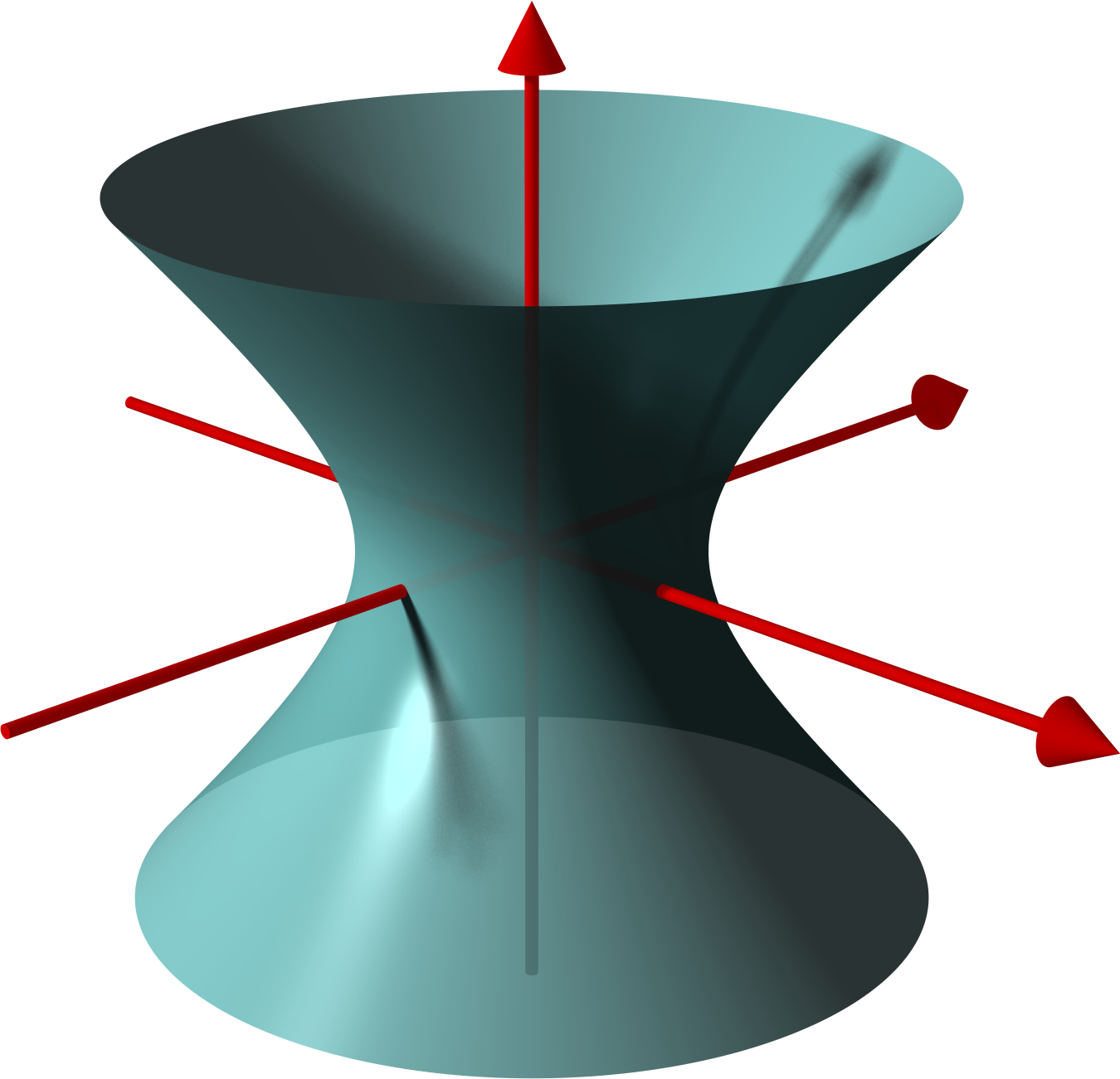
* other

quadric In mathematics, a quadric or quadric surface is a generalization of conic sections (ellipses, parabolas, and hyperbolas). In three-dimensional space, quadrics include ellipsoids, paraboloids, and hyperboloids. More generally, a quadric hype ...

spheroid A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface (mathematics), surface obtained by Surface of revolution, rotating an ellipse about one of its principal axes; in other words, an ellipsoid with t ...

ellipsoid An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional Scaling (geometry), scalings, or more generally, of an affine transformation. An ellipsoid is a quadric surface; that is, a Surface (mathemat ...

paraboloid In geometry, a paraboloid is a quadric surface that has exactly one axial symmetry, axis of symmetry and no central symmetry, center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar p ...

and

hyperboloid In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by def ...

s. Advanced topics include: *

projective geometry In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''p ...

of three dimensions (leading to a proof of

Desargues' theorem In projective geometry, Desargues's theorem, named after Girard Desargues, states: :Two triangles are in perspective ''axially'' if and only if they are in perspective ''centrally''. Denote the three vertices of one triangle by and , and tho ...

by using an extra dimension) * further

polyhedra In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices. The term "polyhedron" may refer either to a solid figure or to its boundary su ...

descriptive geometry Descriptive geometry is the branch of geometry which allows the representation of three-dimensional objects in two dimensions by using a specific set of procedures. The resulting techniques are important for engineering, architecture, design an ...

List of solid figures

Whereas a

is the surface of a

, for other solid figures it is sometimes ambiguous whether the term refers to the surface of the figure or the volume enclosed therein, notably for a

cylinder A cylinder () has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base. A cylinder may also be defined as an infinite ...

Techniques

Various techniques and tools are used in solid geometry. Among them,

analytic geometry In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry. Analytic geometry is used in physics and engineering, and als ...

and

vector Vector most often refers to: * Euclidean vector, a quantity with a magnitude and a direction * Disease vector, an agent that carries and transmits an infectious pathogen into another living organism Vector may also refer to: Mathematics a ...

techniques have a major impact by allowing the systematic use of

linear equations In mathematics, a linear equation is an equation that may be put in the form a_1x_1+\ldots+a_nx_n+b=0, where x_1,\ldots,x_n are the variables (or unknowns), and b,a_1,\ldots,a_n are the coefficients, which are often real numbers. The coefficie ...

and

matrix Matrix (: matrices or matrixes) or MATRIX may refer to: Science and mathematics * Matrix (mathematics), a rectangular array of numbers, symbols or expressions * Matrix (logic), part of a formula in prenex normal form * Matrix (biology), the m ...

algebra, which are important for higher dimensions.

Applications

A major application of solid geometry and stereometry is in

3D computer graphics 3D computer graphics, sometimes called Computer-generated imagery, CGI, 3D-CGI or three-dimensional Computer-generated imagery, computer graphics, are graphics that use a three-dimensional representation of geometric data (often Cartesian coor ...

Notes

References

* Robert Baldwin Hayward (1890
''The Elements of Solid Geometry''
via

Internet Archive The Internet Archive is an American 501(c)(3) organization, non-profit organization founded in 1996 by Brewster Kahle that runs a digital library website, archive.org. It provides free access to collections of digitized media including web ...

* {{DEFAULTSORT:Solid Geometry *

Solid geometry Solid geometry or stereometry is the geometry of Three-dimensional space, three-dimensional Euclidean space (3D space). A solid figure is the region (mathematics), region of 3D space bounded by a two-dimensional closed surface; for example, a ...

History

Topics

List of solid figures

Techniques

Applications

See also

Notes

References