|
Vibronic Transition
Vibronic spectroscopy is a branch of molecular spectroscopy concerned with vibronic transitions: the simultaneous changes in electronic and vibrational energy levels of a molecule due to the absorption or emission of a photon of the appropriate energy. In the gas phase, vibronic transitions are also accompanied by changes in rotational energy. Vibronic spectra of diatomic molecules have been analysed in detail; emission spectra are more complicated than absorption spectra. The intensity of allowed vibronic transitions is governed by the Franck–Condon principle. Vibronic spectroscopy may provide information, such as bond length, on electronic excited states of stable molecules. It has also been applied to the study of unstable molecules such as dicarbon (C2) in discharges, flames and astronomical objects.Hollas, p. 211. Principles Electronic transitions are typically observed in the visible and ultraviolet regions, in the wavelength range approximately 200–700&nb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectroscopy
Spectroscopy is the field of study that measures and interprets electromagnetic spectra. In narrower contexts, spectroscopy is the precise study of color as generalized from visible light to all bands of the electromagnetic spectrum. Spectroscopy, primarily in the electromagnetic spectrum, is a fundamental exploratory tool in the fields of astronomy, chemistry, materials science, and physics, allowing the composition, physical structure and electronic structure of matter to be investigated at the atomic, molecular and macro scale, and over astronomical distances. Historically, spectroscopy originated as the study of the wavelength dependence of the absorption by gas phase matter of visible light dispersed by a prism. Current applications of spectroscopy include biomedical spectroscopy in the areas of tissue analysis and medical imaging. Matter waves and acoustic waves can also be considered forms of radiative energy, and recently gravitational waves have been associa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Interstellar And Circumstellar Molecules
This is a list of molecules that have been detected in the interstellar medium and circumstellar envelopes, grouped by the number of component atoms. The chemical formula is listed for each detected compound, along with any ionized form that has also been observed. Background The molecules listed below were detected through astronomical spectroscopy. Their spectral features arise because molecules either absorb or emit a photon of light when they transition between two molecular energy levels. The energy (and thus the wavelength) of the photon matches the energy difference between the levels involved. Molecular electronic transitions occur when one of the molecule's electrons moves between molecular orbitals, producing a spectral line in the ultraviolet, visible light, optical or near-infrared parts of the electromagnetic spectrum. Alternatively, a vibrational transition transfers Quantum, quanta of energy to (or from) vibrations of molecular bonds, producing signatures in the m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Photodissociation
Photodissociation, photolysis, photodecomposition, or photofragmentation is a chemical reaction in which molecules of a chemical compound are broken down by absorption of light or photons. It is defined as the interaction of one or more photons with one target molecule that dissociates into two fragments. Here, “light” is broadly defined as radiation spanning the vacuum ultraviolet (VUV), ultraviolet (UV), visible, and infrared (IR) regions of the electromagnetic spectrum. To break covalent bonds, photon energies corresponding to visible, UV, or VUV light are typically required, whereas IR photons may be sufficiently energetic to detach ligands from coordination complexes or to fragment supramolecular complexes. Photolysis in photosynthesis Photolysis is part of the light-dependent reaction, light phase, photochemical phase, or Hill reaction of photosynthesis. The general reaction of photosynthetic photolysis can be given in terms of photons as: :\ce + 2 \text \longrigh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Line
A spectral line is a weaker or stronger region in an otherwise uniform and continuous spectrum. It may result from emission (electromagnetic radiation), emission or absorption (electromagnetic radiation), absorption of light in a narrow frequency range, compared with the nearby frequencies. Spectral lines are often used to identify atoms and molecules. These "fingerprints" can be compared to the previously collected ones of atoms and molecules, and are thus used to identify the atomic and molecular components of stars and planets, which would otherwise be impossible. Types of line spectra Spectral lines are the result of interaction between a Quantum mechanics, quantum system (usually atoms, but sometimes molecules or atomic nucleus, atomic nuclei) and a single photon. When a photon has about the right amount of photon energy, energy (which is connected to its frequency) to allow a change in the energy state of the system (in the case of an atom this is usually an electron cha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
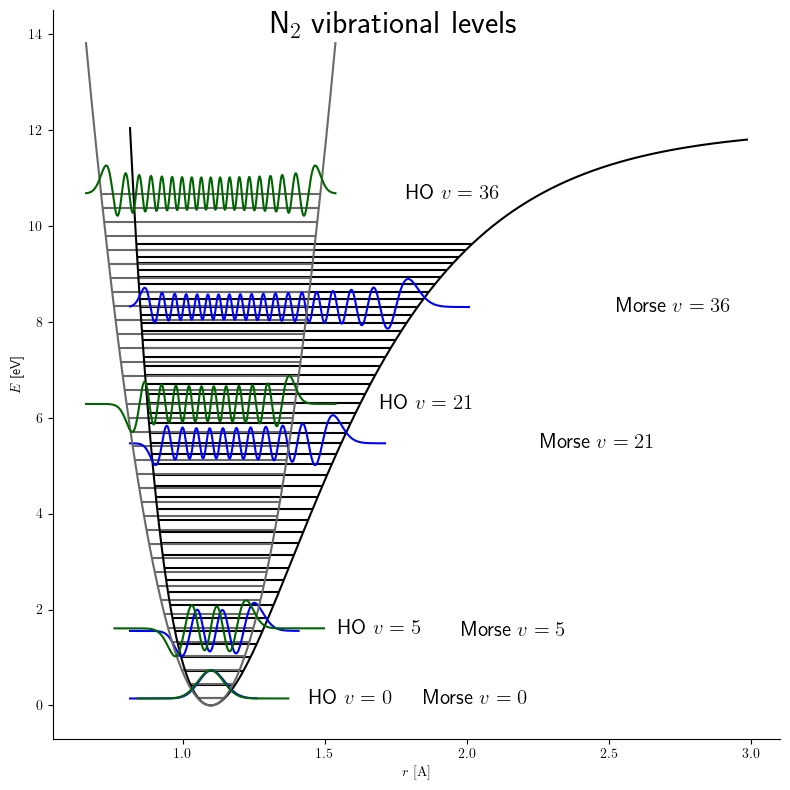
Morse Potential
The Morse potential, named after physicist Philip M. Morse, is a convenient Interatomic potential, interatomic interaction model for the potential energy of a diatomic molecule. It is a better approximation for the oscillation, vibrational structure of the molecule than the quantum harmonic oscillator because it explicitly includes the effects of bond breaking, such as the existence of unbound states. It also accounts for the anharmonicity of real bonds and the non-zero transition probability for overtone band, overtone and Hot band#Combination bands, combination bands. The Morse potential can also be used to model other interactions such as the interaction between an atom and a surface. Due to its simplicity (only three fitting parameters), it is not used in modern spectroscopy. However, its mathematical form inspired the MLR (Morse/Long-range potential, Morse/Long-range) potential, which is the most popular potential energy function used for fitting spectroscopic data. Potential ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anharmonicity
In classical mechanics, anharmonicity is the deviation of a system from being a harmonic oscillator. An oscillator that is not oscillating in harmonic motion is known as an anharmonic oscillator where the system can be approximated to a harmonic oscillator and the anharmonicity can be calculated using perturbation theory. If the anharmonicity is large, then other numerical techniques have to be used. In reality all oscillating systems are anharmonic, but most approximate the harmonic oscillator the smaller the amplitude of the oscillation is. As a result, oscillations with frequencies 2\omega and 3\omega etc., where \omega is the fundamental frequency of the oscillator, appear. Furthermore, the frequency \omega deviates from the frequency \omega_0 of the harmonic oscillations. See also intermodulation and combination tones. As a first approximation, the frequency shift \Delta \omega=\omega-\omega_0 is proportional to the square of the oscillation amplitude A: :\Delta \omeg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Harmonic Oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary smooth potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known. One-dimensional harmonic oscillator Hamiltonian and energy eigenstates The Hamiltonian of the particle is: \hat H = \frac + \frac k ^2 = \frac + \frac m \omega^2 ^2 \, , where is the particle's mass, is the force constant, \omega = \sqrt is the angular frequency of the oscillator, \hat is the position operator (given by in the coordinate basis), and \hat is the momentum operator (given by \hat p = -i \hbar \, \partial / \partial x in the coordinate basis). The first term in the Hamiltonian represents the kinetic energy of the particle, and the second ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Born–Oppenheimer Approximation
In quantum chemistry and molecular physics, the Born–Oppenheimer (BO) approximation is the assumption that the wave functions of atomic nuclei and electrons in a molecule can be treated separately, based on the fact that the nuclei are much heavier than the electrons. Due to the larger relative mass of a nucleus compared to an electron, the coordinates of the nuclei in a system are approximated as fixed, while the coordinates of the electrons are dynamic. The approach is named after Max Born and his 23-year-old graduate student J. Robert Oppenheimer, the latter of whom proposed it in 1927 during a period of intense ferment in the development of quantum mechanics. The approximation is widely used in quantum chemistry to speed up the computation of molecular wavefunctions and other properties for large molecules. There are cases where the assumption of separable motion no longer holds, which make the approximation lose validity (it is said to "break down"), but even then the ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy Level
A quantum mechanics, quantum mechanical system or particle that is bound state, bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical mechanics, classical particles, which can have any amount of energy. The term is commonly used for the energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the atomic nucleus, nucleus, but can also refer to energy levels of nuclei or molecular vibration, vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be Quantization (physics), quantized. In chemistry and atomic physics, an electron shell, or principal energy level, may be thought of as the orbit of one or more electrons around an atom's atomic nucleus, nucleus. The closest shell to the nucleus is called the "1 shell" (also called "K shell"), followed by the "2 shell" (or "L shell"), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Function
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter), psi, respectively). Wave functions are complex number, complex-valued. For example, a wave function might assign a complex number to each point in a region of space. The Born rule provides the means to turn these complex probability amplitudes into actual probabilities. In one common form, it says that the squared modulus of a wave function that depends upon position is the probability density function, probability density of measurement in quantum mechanics, measuring a particle as being at a given place. The integral of a wavefunction's squared modulus over all the system's degrees of freedom must be equal to 1, a condition called ''normalization''. Since the wave function is complex-valued, only its relative phase and relative magnitud ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |