|
Tautochrone
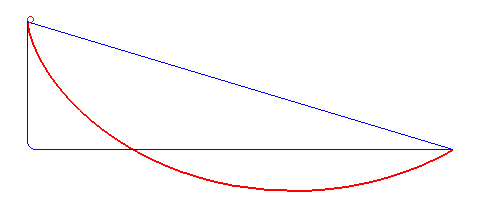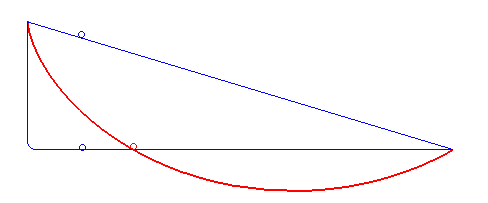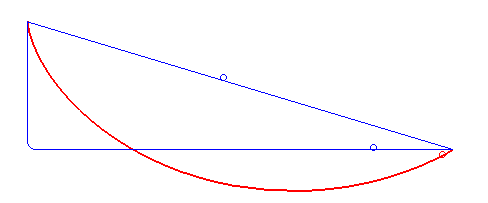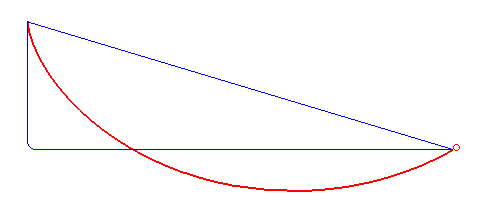
A tautochrone curve or isochrone curve () is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point on the curve. The curve is a cycloid, and the time is equal to Pi, π times the square root of the radius of the circle which generates the cycloid, over the Gravitational acceleration, acceleration of gravity. The tautochrone curve is related to the brachistochrone curve, which is also a cycloid. The tautochrone problem The tautochrone problem, the attempt to identify this curve, was solved by Christiaan Huygens in 1659. He proved geometrically in his ''Horologium Oscillatorium'', originally published in 1673, that the curve is a cycloid. The cycloid is given by a point on a circle of radius r tracing a curve as the circle rolls along the x axis, as: \begin x &= r(\theta - \sin \theta) \\ y &= r(1 - \cos \theta), \end Huygens also proved that the time of descent is equal to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brachistochrone Curve
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly under the influence of a uniform gravitational field to a given end point in the shortest time. The problem was posed by Johann Bernoulli in 1696 and solved by Isaac Newton in 1697. The brachistochrone curve is the same shape as the tautochrone curve; both are cycloids. However, the portion of the cycloid used for each of the two varies. More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a cusp. In contrast, the tautochrone problem can use only up to the first half rotation, and always ends at the horizontal.Stewart, James. "Section 10.1 - Curves Defined by Parametric Equations." ''Calculus: Early Transcendentals''. 7th ed. Belmont, CA: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Christiaan Huygens
Christiaan Huygens, Halen, Lord of Zeelhem, ( , ; ; also spelled Huyghens; ; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution. In physics, Huygens made seminal contributions to optics and mechanics, while as an astronomer he studied the rings of Saturn and discovered its largest moon, Titan (moon), Titan. As an engineer and inventor, he improved the design of telescopes and invented the pendulum clock, the most accurate timekeeper for almost 300 years. A talented mathematician and physicist, his works contain the first idealization of a physical problem by a set of Mathematical model, mathematical parameters, and the first mathematical and mechanistic explanation of an unobservable physical phenomenon.Dijksterhuis, F.J. (2008) Stevin, Huygens and the Dutch republic. ''Nieuw archief voor wiskunde'', ''5'', pp. 100–10/ref> Huygens first identified the correct la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
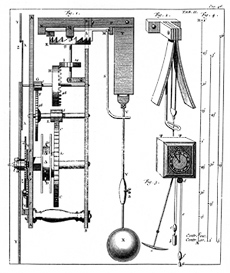
Horologium Oscillatorium
(English language, English: ''The Pendulum Clock: or Geometrical Demonstrations Concerning the Motion of Pendula as Applied to Clocks'') is a book published by Dutch mathematician and physicist Christiaan Huygens in 1673 and his major work on pendulum, pendula and horology. It is regarded as one of the three most important works on mechanics in the 17th century, the other two being Galileo Galilei, Galileo’s ''Discourses and Mathematical Demonstrations Relating to Two New Sciences'' (1638) and Isaac Newton, Newton’s (1687). Much more than a mere description of clocks, Huygens's is the first modern treatise in which a physical problem (the Acceleration, accelerated motion of a falling body) is Mathematical model, idealized by a set of Parameter, parameters then analyzed mathematically and constitutes one of the seminal works of applied mathematics.Bruce, I. (2007). Christian Huygens: Horologium Oscillatorium'. Translated and annotated by Ian Bruce. The book is also known fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it Rolling, rolls along a Line (geometry), straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette (curve), roulette, a curve generated by a curve rolling on another curve. The cycloid, with the Cusp (singularity), cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the Frequency, period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). In physics, when a charged particle at rest is put under a uniform Electric field, electric and magnetic field perpendicular to one another, the particle’s trajectory draws out a cycloid. History The cycloid has been called "The Helen of Geometers" as, like Helen of Troy, it caused frequent quarrels among 17th-centur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that appeared more than 2000 years ago in Euclid's ''Elements'': "The urvedline is ��the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which ��will leave from its imaginary moving some vestige in length, exempt of any width." This definition of a curve has been formalized in modern mathematics as: ''A curve is the image of an interval to a topological space by a continuous function''. In some contexts, the function that defines the curve is called a ''parametrization'', and the curve is a parametric curve. In this article, these curves are sometimes called ''topological curves'' to distinguish them from more constrained curves su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it Rolling, rolls along a Line (geometry), straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette (curve), roulette, a curve generated by a curve rolling on another curve. The cycloid, with the Cusp (singularity), cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the Frequency, period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). In physics, when a charged particle at rest is put under a uniform Electric field, electric and magnetic field perpendicular to one another, the particle’s trajectory draws out a cycloid. History The cycloid has been called "The Helen of Geometers" as, like Helen of Troy, it caused frequent quarrels among 17th-centur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joseph Louis Lagrange
Joseph-Louis Lagrange (born Giuseppe Luigi LagrangiaJoseph-Louis Lagrange, comte de l’Empire ''Encyclopædia Britannica'' or Giuseppe Ludovico De la Grange Tournier; 25 January 1736 – 10 April 1813), also reported as Giuseppe Luigi Lagrange or Lagrangia, was an Italian and naturalized French , physicist and astronomer. He made significa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrangian Mechanics
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the d'Alembert principle of virtual work. It was introduced by the Italian-French mathematician and astronomer Joseph-Louis Lagrange in his presentation to the Turin Academy of Science in 1760 culminating in his 1788 grand opus, ''Mécanique analytique''. Lagrangian mechanics describes a mechanical system as a pair consisting of a configuration space (physics), configuration space ''M'' and a smooth function L within that space called a ''Lagrangian''. For many systems, , where ''T'' and ''V'' are the Kinetic energy, kinetic and Potential energy, potential energy of the system, respectively. The stationary action principle requires that the Action (physics)#Action (functional), action functional of the system derived from ''L'' must remain at a stationary point (specifically, a Maximum and minimum, maximum, Maximum and minimum, minimum, or Saddle point, saddle point) throughout the time evoluti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arclength
Arc length is the distance between two points along a section of a curve. Development of a formulation of arc length suitable for applications to mathematics and the sciences is a problem in vector calculus and in differential geometry. In the most basic formulation of arc length for a vector valued curve (thought of as the trajectory of a particle), the arc length is obtained by integrating speed, the magnitude of the velocity vector over the curve with respect to time. Thus the length of a continuously differentiable curve (x(t),y(t)), for a\le t\le b, in the Euclidean plane is given as the integral L = \int_a^b \sqrt\,dt, (because \sqrt is the magnitude of the velocity vector (x'(t),y'(t)), i.e., the particle's speed). The defining integral of arc length does not always have a closed-form expression, and numerical integration may be used instead to obtain numerical values of arc length. Determining the length of an irregular arc segment by approximating the arc segment as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isochronous Timing
A sequence of events is isochronous if the events occur regularly, or at equal time intervals. The term ''isochronous'' is used in several technical contexts, but usually refers to the primary subject maintaining a constant period or interval (the reciprocal of frequency), despite variations in other measurable factors in the same system. Isochronous timing is a characteristic of a repeating event whereas synchronous timing refers to the relationship between two or more events. *In dynamical systems theory, an oscillator is called ''isochronous'' if its frequency is independent of its amplitude. *In horology, a mechanical clock or watch is ''isochronous'' if it runs at the same rate regardless of changes in its drive force, so that it keeps correct time as its mainspring unwinds or chain length varies. Isochrony is important in timekeeping devices. Simply put, if a power providing device (e.g. a spring or weight) provides constant torque to the wheel train, it will be isochronou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Harmonic Motion
In mechanics and physics, simple harmonic motion (sometimes abbreviated as ) is a special type of periodic motion an object experiences by means of a restoring force whose magnitude is directly proportional to the distance of the object from an equilibrium position and acts towards the equilibrium position. It results in an oscillation that is described by a sinusoid which continues indefinitely (if uninhibited by friction or any other dissipation of energy). Simple harmonic motion can serve as a mathematical model for a variety of motions, but is typified by the oscillation of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's law. The motion is sinusoidal in time and demonstrates a single resonant frequency. Other phenomena can be modeled by simple harmonic motion, including the motion of a simple pendulum, although for it to be an accurate model, the net force on the object at the end of the pendulum must be proportional to the dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |