|
Random Close Pack
Random close packing (RCP) of spheres is an empirical parameter used to characterize the maximum volume fraction of solid objects obtained when they are packed randomly. For example, when a solid container is filled with grain, shaking the container will reduce the volume taken up by the objects, thus allowing more grain to be added to the container. In other words, shaking increases the density of packed objects. But shaking cannot increase the density indefinitely, a limit is reached, and if this is reached without obvious packing into an ordered structure, such as a regular crystal lattice, this is the empirical random close-packed density for this particular procedure of packing. The random close packing is the highest possible volume fraction out of all possible packing procedures. Experiments and computer simulations have shown that the most compact way to pack hard perfect same-size spheres randomly gives a maximum volume fraction of about 64%, i.e., approximately 64% of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Packing Density
A packing density or packing fraction of a packing in some space is the fraction of the space filled by the figures making up the packing. In simplest terms, this is the ratio of the volume of bodies in a space to the volume of the space itself. In packing problems, the objective is usually to obtain a packing of the greatest possible density. In compact spaces If are measurable subsets of a compact measure space and their interiors pairwise do not intersect, then the collection is a packing in and its packing density is :\eta=\frac. In Euclidean space If the space being packed is infinite in measure, such as Euclidean space, it is customary to define the density as the limit of densities exhibited in balls of larger and larger radii. If is the ball of radius centered at the origin, then the density of a packing is :\eta = \lim_\frac. Since this limit does not always exist, it is also useful to define the upper and lower densities as the limit superior and limit in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its Expected value, mean. A low standard Deviation (statistics), deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range. The standard deviation is commonly used in the determination of what constitutes an outlier and what does not. Standard deviation may be abbreviated SD or std dev, and is most commonly represented in mathematical texts and equations by the lowercase Greek alphabet, Greek letter Sigma, σ (sigma), for the population standard deviation, or the Latin script, Latin letter ''s'', for the sample standard deviation. The standard deviation of a random variable, Sample (statistics), sample, statistical population, data set, or probability distribution is the square root of its variance. (For a finite population, v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
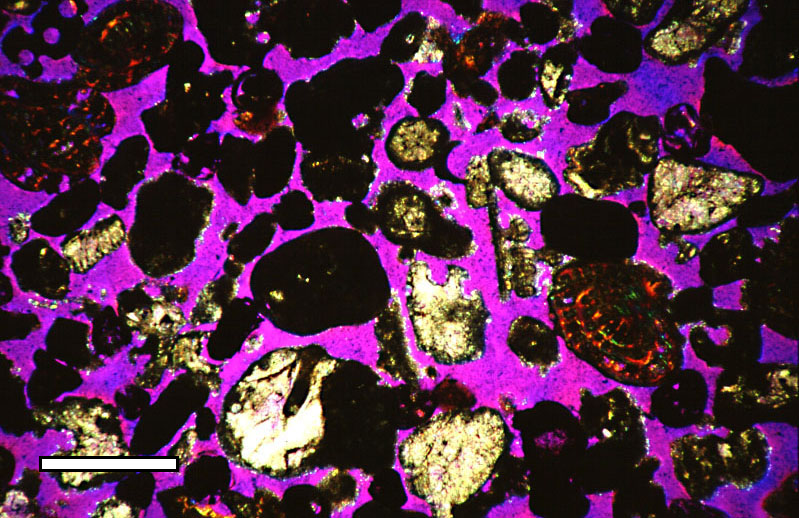
Sphere Packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space. However, sphere packing problems can be generalised to consider unequal spheres, spaces of other dimensions (where the problem becomes circle packing in two dimensions, or hypersphere packing in higher dimensions) or to Non-Euclidean geometry, non-Euclidean spaces such as hyperbolic space. A typical sphere packing problem is to find an arrangement in which the spheres fill as much of the space as possible. The proportion of space filled by the spheres is called the ''packing density'' of the arrangement. As the local density of a packing in an infinite space can vary depending on the volume over which it is measured, the problem is usually to maximise the average or asymptotic density, measured over a large enough volume. For equal spheres in three dimensions, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Porous Media
In materials science, a porous medium or a porous material is a material containing pores (voids). The skeletal portion of the material is often called the "matrix" or "frame". The pores are typically filled with a fluid (liquid or gas). The skeletal material is usually a solid, but structures like foams are often also usefully analyzed using concept of porous media. A porous medium is most often characterised by its porosity. Other properties of the medium (e.g. permeability, tensile strength, electrical conductivity, tortuosity) can sometimes be derived from the respective properties of its constituents (solid matrix and fluid) and the media porosity and pores structure, but such a derivation is usually complex. Even the concept of porosity is only straightforward for a poroelastic medium. Often both the solid matrix and the pore network (also known as the pore space) are continuous, so as to form two interpenetrating continua such as in a sponge. However, there is also a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Close-packing
In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement (or lattice). Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a lattice packing is :\frac \approx 0.74048. The same packing density can also be achieved by alternate stackings of the same close-packed planes of spheres, including structures that are aperiodic in the stacking direction. The Kepler conjecture states that this is the highest density that can be achieved by any arrangement of spheres, either regular or irregular. This conjecture was proven by Thomas Hales. The highest density is so far known only for 1, 2, 3, 8, and 24 dimensions. Many crystal structures are based on a close-packing of a single kind of atom, or a close-packing of large ions with smaller ions filling the spaces between them. The cubic and hexagonal arrangements are very cl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordination Number
In chemistry, crystallography, and materials science, the coordination number, also called ligancy, of a central atom in a molecule or crystal is the number of atoms, molecules or ions bonded to it. The ion/molecule/atom surrounding the central ion/molecule/atom is called a ligand. This number is determined somewhat differently for molecules than for crystals. For molecules and polyatomic ions the coordination number of an atom is determined by simply counting the other atoms to which it is bonded (by either single or multiple bonds). For example, [Cr(NH3)2Cl2Br2]− has Cr3+ as its central cation, which has a coordination number of 6 and is described as ''hexacoordinate''. The common coordination numbers are 4, 6 and 8. Molecules, polyatomic ions and coordination complexes In chemistry, coordination number, defined originally in 1893 by Alfred Werner, is the total number of neighbors of a central atom in a molecule or ion. The concept is most commonly applied to coordination ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Crystal
In crystallography, the cubic (or isometric) crystal system is a crystal system where the Crystal structure#Unit cell, unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of these crystals: *Primitive cubic (abbreviated ''cP'' and alternatively called simple cubic) *Body-centered cubic (abbreviated ''cI'' or bcc) *Face-centered cubic (abbreviated ''cF'' or fcc) Note: the term fcc is often used in synonym for the Close-packing of equal spheres, ''cubic close-packed'' or ccp structure occurring in metals. However, fcc stands for a face-centered cubic Bravais lattice, which is not necessarily close-packed when a motif is set onto the lattice points. E.g. the diamond and the zincblende lattices are fcc but not close-packed. Each is subdivided into other variants listed below. Although the ''unit cells'' in these crystals are conventionally taken to be cubes, the primitive cell, primitiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Packing Density
A packing density or packing fraction of a packing in some space is the fraction of the space filled by the figures making up the packing. In simplest terms, this is the ratio of the volume of bodies in a space to the volume of the space itself. In packing problems, the objective is usually to obtain a packing of the greatest possible density. In compact spaces If are measurable subsets of a compact measure space and their interiors pairwise do not intersect, then the collection is a packing in and its packing density is :\eta=\frac. In Euclidean space If the space being packed is infinite in measure, such as Euclidean space, it is customary to define the density as the limit of densities exhibited in balls of larger and larger radii. If is the ball of radius centered at the origin, then the density of a packing is :\eta = \lim_\frac. Since this limit does not always exist, it is also useful to define the upper and lower densities as the limit superior and limit in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Porosity
Porosity or void fraction is a measure of the void (i.e. "empty") spaces in a material, and is a fraction of the volume of voids over the total volume, between 0 and 1, or as a percentage between 0% and 100%. Strictly speaking, some tests measure the "accessible void", the total amount of void space accessible from the surface (cf. closed-cell foam). There are many ways to test porosity in a substance or part, such as industrial CT scanning. The term porosity is used in multiple fields including pharmaceutics, ceramics, metallurgy, materials, manufacturing, petrophysics, hydrology, earth sciences, soil mechanics, rock mechanics, and engineering. Void fraction in two-phase flow In gas-liquid two-phase flow, the void fraction is defined as the fraction of the flow-channel volume that is occupied by the gas phase or, alternatively, as the fraction of the cross-sectional area of the channel that is occupied by the gas phase. Void fraction usually varies from location to l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
M&M's
M&M's are color-varied sugar-coated dragée chocolate confectionery by the Mars Wrigley Confectionery division of Mars Inc.. The candy consists of a candy shell surrounding a filling which determines the specific type of M&M's. Each piece has the letter "m" printed in lower case in white on one side. They are produced in different colors, some of which have changed over the years. The original candy has a semi-sweet chocolate filling which, upon introduction of other variations, was branded as the "plain, normal" variety. Peanut M&M's, which feature a peanut coated in milk chocolate, and finally a candy shell, were the first variation to be introduced, and they remain a regular variety. Numerous other variations have been introduced, some of which are regular widespread varieties (peanut butter, almond, pretzel, crispy, dark chocolate, and caramel) while others are limited in duration or geographic availability. The candy originated in the United States in 1941, and M&M's hav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polydispersed
In chemistry, the dispersity is a measure of the heterogeneity of sizes of molecules or particles in a mixture. A collection of objects is called uniform if the objects have the same size, shape, or mass. A sample of objects that have an inconsistent size, shape and mass distribution is called non-uniform. The objects can be in any form of chemical dispersion, such as particles in a colloid, droplets in a cloud, crystals in a rock, or polymer macromolecules in a solution or a solid polymer mass. Polymers can be described by molecular mass distribution; a population of particles can be described by size, surface area, and/or mass distribution; and thin films can be described by film thickness distribution. IUPAC has deprecated the use of the term ''polydispersity index'', having replaced it with the term ''dispersity'', represented by the symbol Đ (pronounced D-strokeStepto, R. F. T.; Gilbert, R. G.; Hess, M.; Jenkins, A. D.; Jones, R. G.; Kratochvíl P. (2009).Dispersity in Po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid
Solid is a state of matter where molecules are closely packed and can not slide past each other. Solids resist compression, expansion, or external forces that would alter its shape, with the degree to which they are resisted dependent upon the specific material under consideration. Solids also always possess the least amount of kinetic energy per atom/molecule relative to other phases or, equivalently stated, solids are formed when matter in the liquid / gas phase is cooled below a certain temperature. This temperature is called the melting point of that substance and is an intrinsic property, i.e. independent of how much of the matter there is. All matter in solids can be arranged on a microscopic scale under certain conditions. Solids are characterized by structural rigidity and resistance to applied external forces and pressure. Unlike liquids, solids do not flow to take on the shape of their container, nor do they expand to fill the entire available volume like a gas. Much ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |