|
Mathematical Diagram
Mathematical diagrams, such as charts and graphs, are mainly designed to convey mathematical relationships—for example, comparisons over time. Specific types of mathematical diagrams Argand diagram A complex number can be visually represented as a pair of numbers forming a vector on a diagram called an Argand diagram The complex plane is sometimes called the ''Argand plane'' because it is used in ''Argand diagrams''. These are named after Jean-Robert Argand (1768–1822), although they were first described by Norwegian-Danish land surveyor and mathematician Caspar Wessel (1745–1818). Argand diagrams are frequently used to plot the positions of the poles and zeroes of a function in the complex plane. The concept of the complex plane allows a geometric interpretation of complex numbers. Under addition, they add like vectors. The multiplication of two complex numbers can be expressed most easily in polar coordinates — the magnitude or ''modulus'' of the product is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclid Lueneburg Ms Page 8
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely dominated the field until the early 19th century. His system, now referred to as Euclidean geometry, involved innovations in combination with a synthesis of theories from earlier Greek mathematicians, including Eudoxus of Cnidus, Hippocrates of Chios, Thales and Theaetetus. With Archimedes and Apollonius of Perga, Euclid is generally considered among the greatest mathematicians of antiquity, and one of the most influential in the history of mathematics. Very little is known of Euclid's life, and most information comes from the scholars Proclus and Pappus of Alexandria many centuries later. Medieval Islamic mathematicians invented a fanciful biography, and medieval Byzantine and early Renaissance scholars mistook him for the earlier philosopher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polar Coordinates
In mathematics, the polar coordinate system specifies a given point (mathematics), point in a plane (mathematics), plane by using a distance and an angle as its two coordinate system, coordinates. These are *the point's distance from a reference point called the ''pole'', and *the point's direction from the pole relative to the direction of the ''polar axis'', a ray (geometry), ray drawn from the pole. The distance from the pole is called the ''radial coordinate'', ''radial distance'' or simply ''radius'', and the angle is called the ''angular coordinate'', ''polar angle'', or ''azimuth''. The pole is analogous to the origin in a Cartesian coordinate system. Polar coordinates are most appropriate in any context where the phenomenon being considered is inherently tied to direction and length from a center point in a plane, such as spirals. Planar physical systems with bodies moving around a central point, or phenomena originating from a central point, are often simpler and more in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Object (category Theory)
In mathematics, a category (sometimes called an abstract category to distinguish it from a concrete category) is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions. ''Category theory'' is a branch of mathematics that seeks to generalize all of mathematics in terms of categories, independent of what their objects and arrows represent. Virtually every branch of modern mathematics can be described in terms of categories, and doing so often reveals deep insights and similarities between seemingly different areas of mathematics. As such, category theory provides an alternative foundation for mathematics to set theory and other proposed axiomatic foundations. In general, the objects and arrows may be abstract entities of any kind, and the n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category Theory
Category theory is a general theory of mathematical structures and their relations. It was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Category theory is used in most areas of mathematics. In particular, many constructions of new mathematical objects from previous ones that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient space (other), quotient spaces, direct products, completion, and duality (mathematics), duality. Many areas of computer science also rely on category theory, such as functional programming and Semantics (computer science), semantics. A category (mathematics), category is formed by two sorts of mathematical object, objects: the object (category theory), objects of the category, and the morphisms, which relate two objects called the ''source'' and the ''target'' of the morphism. Metapho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
5 Lemma
In mathematics, especially homological algebra and other applications of abelian category theory, the five lemma is an important and widely used lemma (mathematics), lemma about commutative diagrams. The five lemma is not only valid for abelian categories but also works in the category of groups, for example. The five lemma can be thought of as a combination of two other theorems, the four lemmas, which are duality (category theory), dual to each other. Statements Consider the following commutative diagram in any abelian category (such as the category of abelian groups or the category of vector spaces over a given field (algebra), field) or in the category of group (mathematics), groups. : file:5 lemma.svg The five lemma states that, if the rows are exact sequence, exact, ''m'' and ''p'' are isomorphisms, ''l'' is an epimorphism, and ''q'' is a monomorphism, then ''n'' is also an isomorphism. The two four-lemmas state: Proof The method of proof we shall use is commonly referred ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Morpho (genus)
The morpho butterflies comprise many species of Neotropical butterfly under the genus ''Morpho''. This genus includes more than 29 species problem, accepted species and 147 accepted subspecies, found mostly in South America, Mexico, and Central America. ''Morpho'' wingspans range from for ''Morpho rhodopteron, M. rhodopteron'' to for ''M. hecuba'', the imposing sunset morpho. The name ''morpho'', meaning "changed" or "modified", is also an epithet. Blue morphos are severely threatened by the deforestation of tropical forests and habitat fragmentation. Humans provide a direct threat to this genus because their beauty attracts artists and collectors from all over the globe who wish to capture and display them. Aside from humans, birds like the jacamar and flycatcher are the adult butterfly’s natural predators. Taxonomy and nomenclature Many names attach to the genus ''Morpho''. The genus has also been divided into subgenera. Hundreds of form, variety, and aberration names are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Butterfly
Butterflies are winged insects from the lepidopteran superfamily Papilionoidea, characterized by large, often brightly coloured wings that often fold together when at rest, and a conspicuous, fluttering flight. The oldest butterfly fossils have been dated to the Paleocene, about 56 million years ago, though molecular evidence suggests that they likely originated in the Cretaceous. Butterflies have a four-stage life cycle, and like other holometabolous insects they undergo complete metamorphosis. Winged adults lay eggs on the food plant on which their larvae, known as caterpillars, will feed. The caterpillars grow, sometimes very rapidly, and when fully developed, pupate in a chrysalis. When metamorphosis is complete, the pupal skin splits, the adult insect climbs out, expands its wings to dry, and flies off. Some butterflies, especially in the tropics, have several generations in a year, while others have a single generation, and a few in cold locations may take s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cooley–Tukey FFT Algorithm
The Cooley–Tukey algorithm, named after James Cooley, J. W. Cooley and John Tukey, is the most common fast Fourier transform (FFT) algorithm. It re-expresses the discrete Fourier transform (DFT) of an arbitrary composite number, composite size N = N_1N_2 in terms of ''N''1 smaller DFTs of sizes ''N''2, recursion, recursively, to reduce the computation time to O(''N'' log ''N'') for highly composite ''N'' (smooth numbers). Because of the algorithm's importance, specific variants and implementation styles have become known by their own names, as described below. Because the Cooley–Tukey algorithm breaks the DFT into smaller DFTs, it can be combined arbitrarily with any other algorithm for the DFT. For example, Rader's FFT algorithm, Rader's or Bluestein's FFT algorithm, Bluestein's algorithm can be used to handle large prime factors that cannot be decomposed by Cooley–Tukey, or the prime-factor FFT algorithm, prime-factor algorithm can be exploited for greater efficiency in s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Butterfly Diagram
In the context of fast Fourier transform algorithms, a butterfly is a portion of the computation that combines the results of smaller discrete Fourier transforms (DFTs) into a larger DFT, or vice versa (breaking a larger DFT up into subtransforms). The name "butterfly" comes from the shape of the data-flow diagram in the radix-2 case, as described below.Alan V. Oppenheim, Ronald W. Schafer, and John R. Buck, ''Discrete-Time Signal Processing'', 2nd edition (Upper Saddle River, NJ: Prentice Hall, 1989) The earliest occurrence in print of the term is thought to be in a 1969 MIT technical report. The same structure can also be found in the Viterbi algorithm, used for finding the most likely sequence of hidden states. Most commonly, the term "butterfly" appears in the context of the Cooley–Tukey FFT algorithm, which recursively breaks down a DFT of composite size ''n'' = ''rm'' into ''r'' smaller transforms of size ''m'' where ''r'' is the "radix" of the transform. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
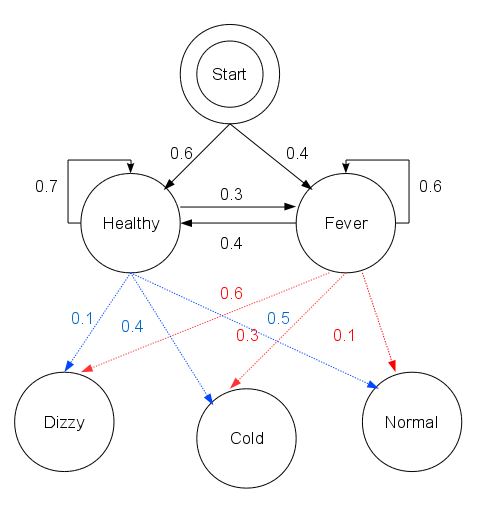
Viterbi Algorithm
The Viterbi algorithm is a dynamic programming algorithm for obtaining the maximum a posteriori probability estimate of the most likely sequence of hidden states—called the Viterbi path—that results in a sequence of observed events. This is done especially in the context of Markov information sources and hidden Markov models (HMM). The algorithm has found universal application in decoding the convolutional codes used in both CDMA and GSM digital cellular, dial-up modems, satellite, deep-space communications, and 802.11 wireless LANs. It is now also commonly used in speech recognition, speech synthesis, diarization, keyword spotting, computational linguistics, and bioinformatics. For example, in speech-to-text (speech recognition), the acoustic signal is treated as the observed sequence of events, and a string of text is considered to be the "hidden cause" of the acoustic signal. The Viterbi algorithm finds the most likely string of text given the acoustic signal. His ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Fourier Transform
In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced Sampling (signal processing), samples of a function (mathematics), function into a same-length sequence of equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a complex number, complex-valued function of frequency. The interval at which the DTFT is sampled is the reciprocal of the duration of the input sequence. An inverse DFT (IDFT) is a Fourier series, using the DTFT samples as coefficients of complex number, complex Sine wave, sinusoids at the corresponding DTFT frequencies. It has the same sample-values as the original input sequence. The DFT is therefore said to be a frequency domain representation of the original input sequence. If the original sequence spans all the non-zero values of a function, its DTFT is continuous (and periodic), and the DFT provides discrete samples of one cycle. If the original sequence is one cycle of a periodic fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Butterfly Diagram
In the context of fast Fourier transform algorithms, a butterfly is a portion of the computation that combines the results of smaller discrete Fourier transforms (DFTs) into a larger DFT, or vice versa (breaking a larger DFT up into subtransforms). The name "butterfly" comes from the shape of the data-flow diagram in the radix-2 case, as described below.Alan V. Oppenheim, Ronald W. Schafer, and John R. Buck, ''Discrete-Time Signal Processing'', 2nd edition (Upper Saddle River, NJ: Prentice Hall, 1989) The earliest occurrence in print of the term is thought to be in a 1969 MIT technical report. The same structure can also be found in the Viterbi algorithm, used for finding the most likely sequence of hidden states. Most commonly, the term "butterfly" appears in the context of the Cooley–Tukey FFT algorithm, which recursively breaks down a DFT of composite size ''n'' = ''rm'' into ''r'' smaller transforms of size ''m'' where ''r'' is the "radix" of the transform. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |