|
Inharmonicity
In music, inharmonicity is the degree to which the frequency, frequencies of overtones (also known as Harmonic series (music)#Partial, partials or partial tones) depart from Integer, whole multiples of the fundamental frequency (harmonic series (music), harmonic series). Acoustically, a note perceived to have a single distinct pitch in fact contains a variety of additional overtones. Many percussion instruments, such as cymbals, tam-tams, and Tubular bells, chimes, create complex and inharmonic sounds. Music harmony and intonation depends strongly on the harmonicity of tones. An ideal, homogeneous, infinitesimally thin or infinitely flexible string or column of air has exact harmonic modes of vibration. In any real musical instrument, the resonant body that produces the music tone—typically a string, wire, or column of air—deviates from this ideal and has some small or large amount of inharmonicity. For instance, a very thick string behaves less as an ideal string and m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
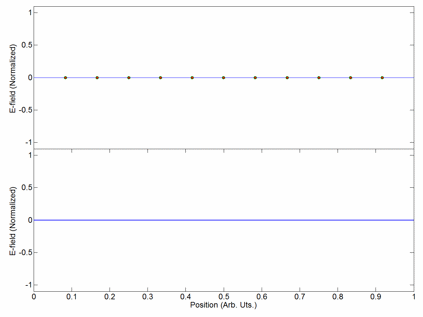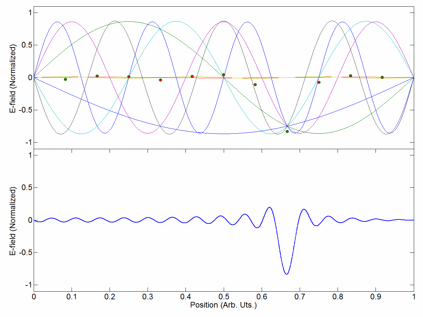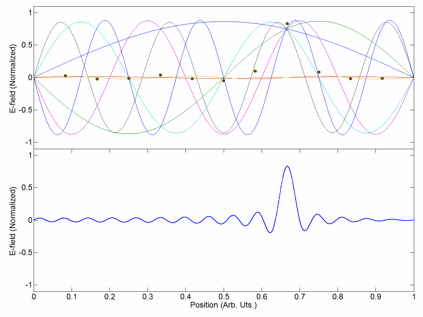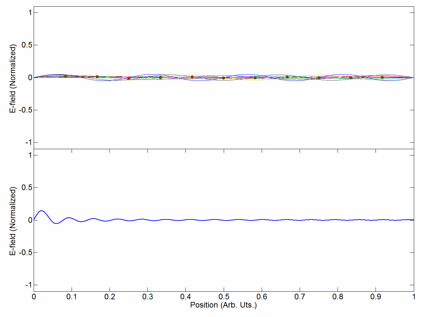
Inharmonic Waveform
In music, inharmonicity is the degree to which the frequencies of overtones (also known as partials or partial tones) depart from whole multiples of the fundamental frequency ( harmonic series). Acoustically, a note perceived to have a single distinct pitch in fact contains a variety of additional overtones. Many percussion instruments, such as cymbals, tam-tams, and chimes, create complex and inharmonic sounds. Music harmony and intonation depends strongly on the harmonicity of tones. An ideal, homogeneous, infinitesimally thin or infinitely flexible string or column of air has exact harmonic modes of vibration. In any real musical instrument, the resonant body that produces the music tone—typically a string, wire, or column of air—deviates from this ideal and has some small or large amount of inharmonicity. For instance, a very thick string behaves less as an ideal string and more like a cylinder (a tube of mass), which has natural resonances that are not whole num ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stretched Tuning
Stretched tuning is a detail of musical tuning, applied to wire-stringed musical instruments, older, non-digital electric pianos (such as the Fender Rhodes piano and Wurlitzer electric piano), and some sample-based synthesizers based on these instruments, to accommodate the natural inharmonicity of their vibrating elements. In stretched tuning, two notes an octave apart, whose fundamental frequencies theoretically have an exact 2:1 ratio, are tuned slightly farther apart (a stretched octave). If the frequency ratios of octaves are greater than a factor of 2, the tuning is ''stretched''; if smaller than a factor of 2, it is ''compressed''." ''Melodic stretch'' refers to tunings with fundamentals stretched relative to each other, while ''harmonic stretch'' refers to tunings with harmonics stretched relative to fundamentals which are not stretched.Hartmann (1997), p.276. For example, the piano features both stretched harmonics and, to accommodate those, stretched fundamentals. Fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Spectra Theoretical X Y
In physics, acoustics, and telecommunications, a harmonic is a sinusoidal wave with a frequency that is a positive integer multiple of the ''fundamental frequency'' of a periodic signal. The fundamental frequency is also called the ''1st harmonic''; the other harmonics are known as ''higher harmonics''. As all harmonics are periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. The set of harmonics forms a '' harmonic series''. The term is employed in various disciplines, including music, physics, acoustics, electronic power transmission, radio technology, and other fields. For example, if the fundamental frequency is 50 Hz, a common AC power supply frequency, the frequencies of the first three higher harmonics are 100 Hz (2nd harmonic), 150 Hz (3rd harmonic), 200 Hz (4th harmonic) and any addition of waves with these frequencies is periodic at 50 Hz. In music, harmonics are used on string instruments and w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pizzicato
Pizzicato (, ; translated as 'pinched', and sometimes roughly as 'plucked') is a playing technique that involves plucking the strings of a string instrument. The exact technique varies somewhat depending on the type of instrument: * On bowed string instruments it is a method of playing by plucking the strings with the fingers, rather than using the bow. This produces a very different sound from bowing, short and percussive rather than sustained. * On keyboard string instruments, such as the piano, pizzicato may be employed (although rarely seen in traditional repertoire, this technique has been normalized in contemporary music, with ample examples by George Crumb, Tōru Takemitsu, Helmut Lachenmann, and others) as one of the variety of techniques involving direct manipulation of the strings known collectively as " string piano". * On the guitar, it is a muted form of plucking, which bears an audible resemblance to pizzicato on a bowed string instrument with its relatively ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mode-locking
Mode locking is a technique in optics by which a laser can be made to produce pulses of light of extremely short duration, on the order of picoseconds (10−12 s) or femtoseconds (10−15 s). A laser operated in this way is sometimes referred to as a femtosecond laser, for example, in modern refractive surgery. The basis of the technique is to induce a fixed phase relationship between the longitudinal modes of the laser's resonant cavity. Constructive interference between these modes can cause the laser light to be produced as a train of pulses. The laser is then said to be "phase-locked" or "mode-locked". Laser cavity modes Although laser light is perhaps the purest form of light, it is not of a single, pure frequency or wavelength. All lasers produce light over some natural bandwidth or range of frequencies. A laser's bandwidth of operation is determined primarily by the gain medium from which the laser is constructed, and the range of frequencies over which a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Series (music)
The harmonic series (also overtone series) is the sequence of harmonics, musical tones, or pure tones whose frequency is an integer multiple of a ''fundamental frequency''. Definite pitch, Pitched musical instruments are often based on an Acoustics, acoustic resonator such as a String (music), string or a column of air, which Oscillation, oscillates at numerous Normal mode, modes simultaneously. As waves travel in both directions along the string or air column, they reinforce and cancel one another to form standing waves. Interaction with the surrounding air produces audible sound waves, which travel away from the instrument. These frequencies are generally integer multiples, or harmonics, of the Fundamental frequency, fundamental and such multiples form the Harmonic series (mathematics), harmonic series. The fundamental, which is usually perceived as the lowest #Partial, partial present, is generally perceived as the Pitch (music), pitch of a musical tone. The musical timbre of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Piano Tuning
Piano tuning is the process of adjusting the tension of the strings of an acoustic piano so that the musical intervals between strings are in tune. The meaning of the term 'in tune', in the context of piano tuning, is not simply a particular fixed set of pitches. Fine piano tuning requires an assessment of the vibration interaction among notes, which is different for every piano, thus in practice requiring slightly different pitches from any theoretical standard. Pianos are usually tuned to a modified version of the system called equal temperament. (See Piano key frequencies for the theoretical piano tuning.) In all systems of tuning, every pitch may be derived from its relationship to a chosen fixed pitch, which is usually A440 (440 Hz), the note A above middle C. For a classical piano and musical theory, the middle C is usually labelled as C4 (as in scientific pitch notation); However, in the MIDI standard definition this middle C (261.626 Hz) is labelled C3. In pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beat (acoustics)
In acoustics, a beat is an interference pattern between two sounds of slightly different frequencies, ''perceived'' as a periodic variation in volume whose rate is the difference of the two frequencies. With tuning instruments that can produce sustained tones, beats can be readily recognized. Tuning two tones to a unison will present a peculiar effect: when the two tones are close in pitch but not identical, the difference in frequency generates the beating. The volume varies as in a tremolo as the sounds alternately interfere constructively and destructively. As the two tones gradually approach unison, the beating slows down and may become so slow as to be imperceptible. As the two tones get further apart, their beat frequency starts to approach the range of human pitch perception, the beating starts to sound like a note, and a combination tone is produced. Mathematics and physics of beat tones This phenomenon is best known in acoustics or music, though it can be found in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Synthesizer
A synthesizer (also synthesiser or synth) is an electronic musical instrument that generates audio signals. Synthesizers typically create sounds by generating waveforms through methods including subtractive synthesis, additive synthesis and frequency modulation synthesis. These sounds may be altered by components such as filters, which cut or boost frequencies; envelopes, which control articulation, or how notes begin and end; and low-frequency oscillators, which modulate parameters such as pitch, volume, or filter characteristics affecting timbre. Synthesizers are typically played with keyboards or controlled by sequencers, software or other instruments, and may be synchronized to other equipment via MIDI. Synthesizer-like instruments emerged in the United States in the mid-20th century with instruments such as the RCA Mark II, which was controlled with punch cards and used hundreds of vacuum tubes. The Moog synthesizer, developed by Robert Moog and first so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standing Wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect to time, and the oscillations at different points throughout the wave are in phase. The locations at which the absolute value of the amplitude is minimum are called node (physics), nodes, and the locations where the absolute value of the amplitude is maximum are called antinodes. Standing waves were first described scientifically by Michael Faraday in 1831. Faraday observed Faraday wave, standing waves on the surface of a liquid in a vibrating container. Franz Melde coined the term "standing wave" (German: ''stehende Welle'' or ''Stehwelle'') around 1860 and demonstrated the phenomenon in his classic experiment with vibrating strings. This phenomenon can occur because the medium is moving in the direction opposite to the movement of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dispersion Relation
In the physical sciences and electrical engineering, dispersion relations describe the effect of dispersion on the properties of waves in a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the dispersion relation, one can calculate the frequency-dependent phase velocity and group velocity of each sinusoidal component of a wave in the medium, as a function of frequency. In addition to the geometry-dependent and material-dependent dispersion relations, the overarching Kramers–Kronig relations describe the frequency-dependence of wave propagation and attenuation. Dispersion may be caused either by geometric boundary conditions ( waveguides, shallow water) or by interaction of the waves with the transmitting medium. Elementary particles, considered as matter waves, have a nontrivial dispersion relation, even in the absence of geometric constraints and other media. In the presence of dispersion, a wave does not propagate with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |