|
Empirical Process
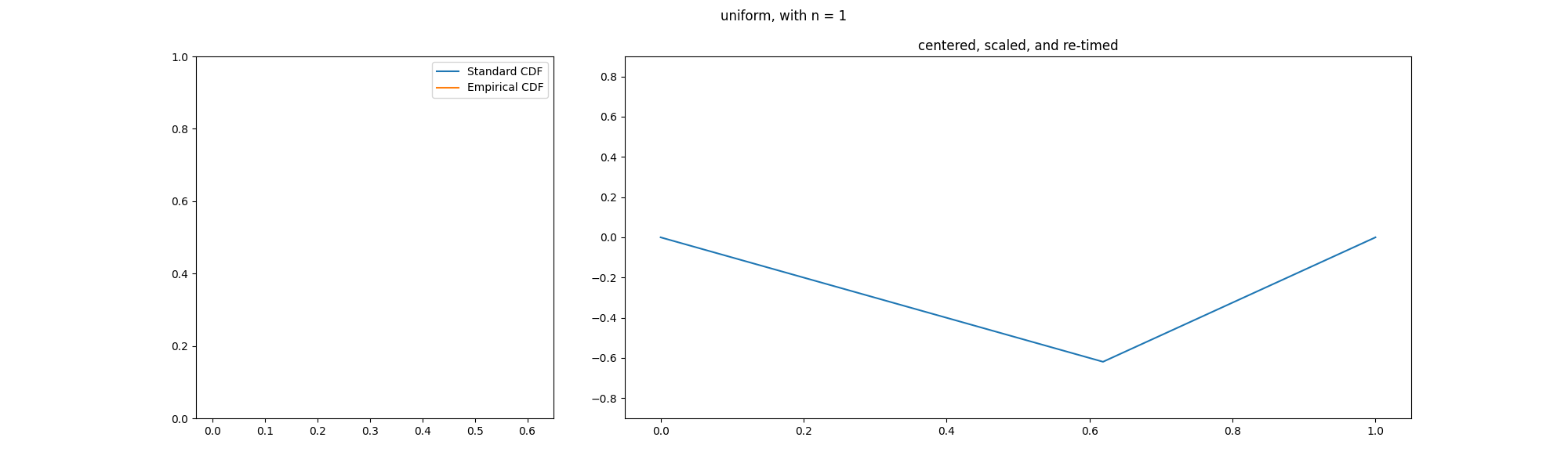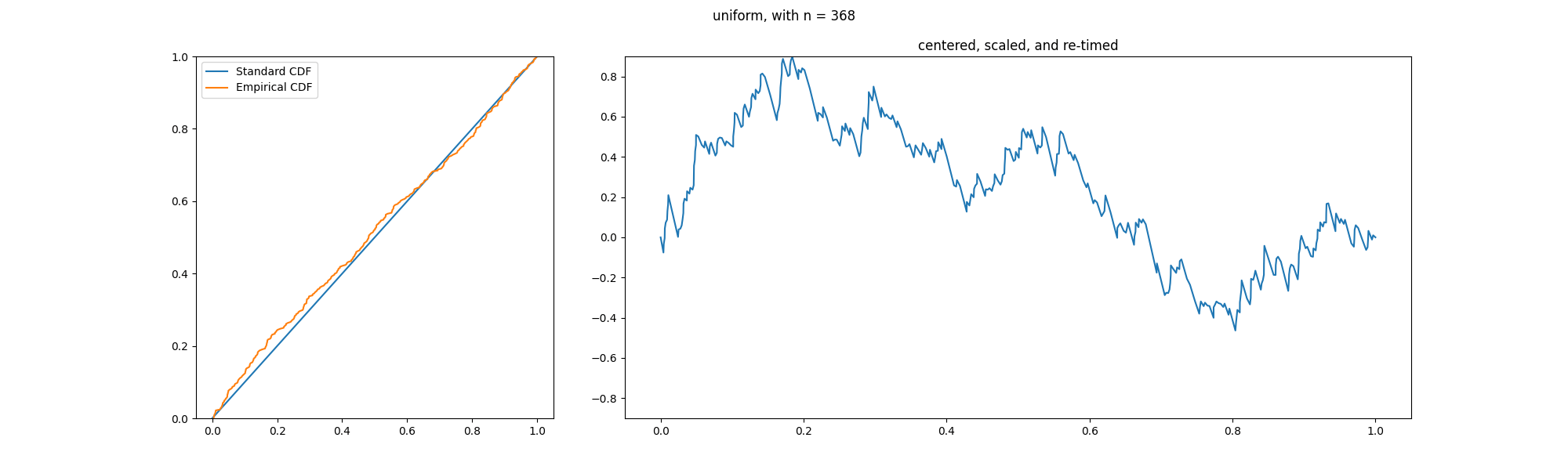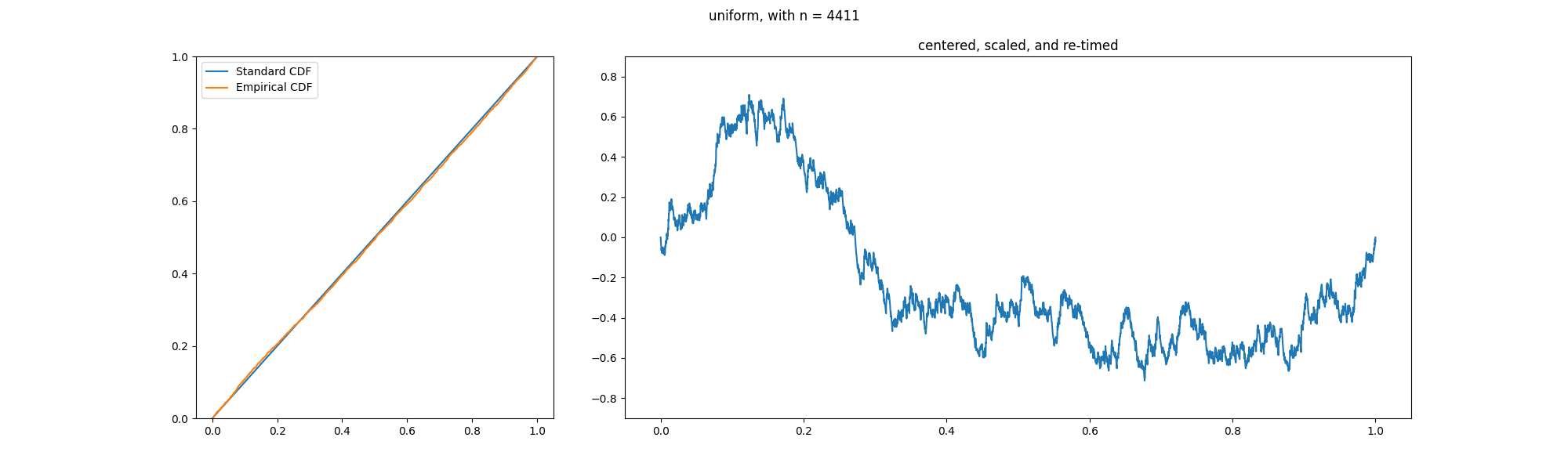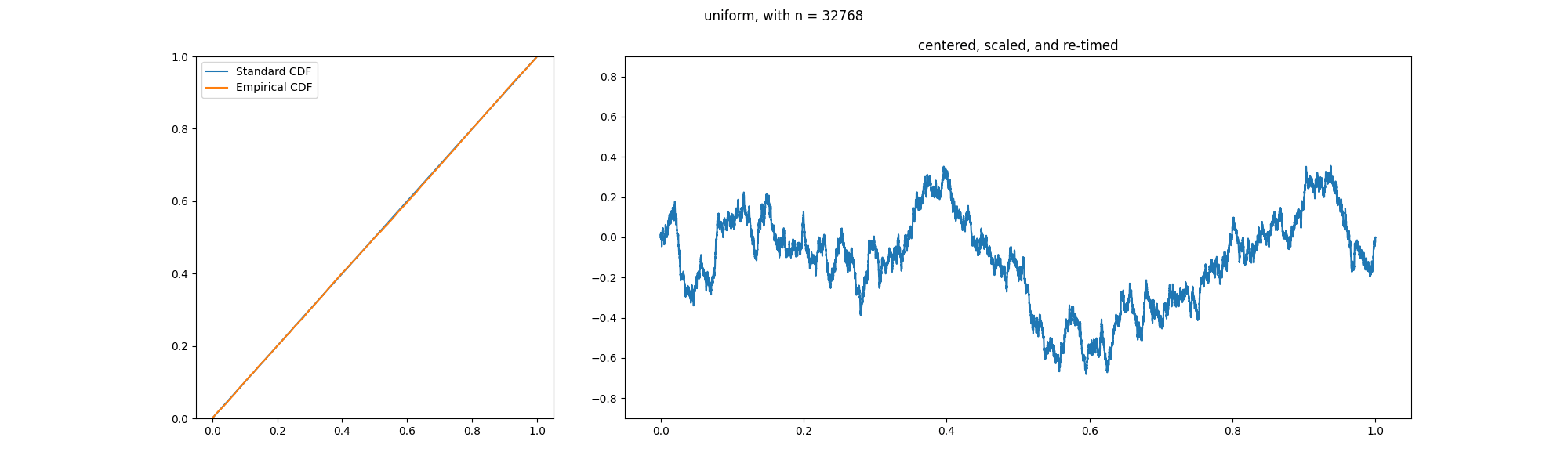
In probability theory, an empirical process is a stochastic process that characterizes the deviation of the empirical distribution function from its expectation. In mean field theory, limit theorems (as the number of objects becomes large) are considered and generalise the central limit theorem for empirical measures. Applications of the theory of empirical processes arise in non-parametric statistics. Definition For ''X''1, ''X''2, ... ''X''''n'' independent and identically-distributed random variables in R with common cumulative distribution function ''F''(''x''), the empirical distribution function is defined by :F_n(x)=\frac\sum_^n I_(X_i), where I''C'' is the indicator function of the set ''C''. For every (fixed) ''x'', ''F''''n''(''x'') is a sequence of random variables which converge to ''F''(''x'') almost surely by the strong law of large numbers. That is, ''F''''n'' converges to ''F'' pointwise. Glivenko and Cantelli strengthened this result by proving uniform convergenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glivenko–Cantelli Theorem
In the theory of probability, the Glivenko–Cantelli theorem (sometimes referred to as the fundamental theorem of statistics), named after Valery Ivanovich Glivenko and Francesco Paolo Cantelli, describes the asymptotic behaviour of the empirical distribution function as the number of Independent and identically distributed random variables, independent and identically distributed observations grows. Specifically, the empirical distribution function Uniform convergence, converges uniformly to the true distribution function almost surely. The uniform convergence of more general empirical measures becomes an important property of the Glivenko–Cantelli classes of functions or sets. The Glivenko–Cantelli classes arise in Vapnik–Chervonenkis theory, with applications to machine learning. Applications can be found in econometrics making use of M-estimators. Statement Assume that X_1,X_2,\dots are independent and identically distributed random variables in \mathbb with commo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Khmaladze Transformation
In statistics, the Khmaladze transformation is a mathematical tool used in constructing convenient goodness of fit tests for hypothetical distribution functions. More precisely, suppose X_1,\ldots, X_n are i.i.d., possibly multi-dimensional, random observations generated from an unknown probability distribution. A classical problem in statistics is to decide how well a given hypothetical distribution function F, or a given hypothetical parametric family of distribution functions \, fits the set of observations. The Khmaladze transformation allows us to construct goodness of fit tests with desirable properties. It is named after Estate V. Khmaladze. Consider the sequence of empirical distribution functions F_n based on a sequence of i.i.d random variables, X_1,\ldots, X_n, as ''n'' increases. Suppose F is the hypothetical distribution function of each X_i. To test whether the choice of F is correct or not, statisticians use the normalized difference, : v_n(x)=\sqrt _n(x)-F(x) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brownian Bridge
A Brownian bridge is a continuous-time gaussian process ''B''(''t'') whose probability distribution is the conditional probability distribution of a standard Wiener process ''W''(''t'') (a mathematical model of Brownian motion) subject to the condition (when standardized) that ''W''(''T'') = 0, so that the process is pinned to the same value at both ''t'' = 0 and ''t'' = ''T''. More precisely: : B_t := (W_t\mid W_T=0),\;t \in ,T The expected value of the bridge at any t in the interval ,T/math> is zero, with variance \frac, implying that the most uncertainty is in the middle of the bridge, with zero uncertainty at the nodes. The covariance of ''B''(''s'') and ''B''(''t'') is \min(s,t)-\frac, or \frac if s . It is independent of W(T) Conversely, if B(t) is a Brownian bridge for t \in , 1/math> and Z is a standard normal random variable independent of B, then the process : W(t) = B(t) + tZ\, is a Wiener process for t \in , 1/math>. More generally, a Wiener ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weak Convergence Of Measures
In mathematics, more specifically measure theory, there are various notions of the convergence of measures. For an intuitive general sense of what is meant by ''convergence of measures'', consider a sequence of measures on a space, sharing a common collection of measurable sets. Such a sequence might represent an attempt to construct 'better and better' approximations to a desired measure that is difficult to obtain directly. The meaning of 'better and better' is subject to all the usual caveats for taking limits; for any error tolerance we require there be sufficiently large for to ensure the 'difference' between and is smaller than . Various notions of convergence specify precisely what the word 'difference' should mean in that description; these notions are not equivalent to one another, and vary in strength. Three of the most common notions of convergence are described below. Informal descriptions This section attempts to provide a rough intuitive description of three ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Process
In probability theory and statistics, a Gaussian process is a stochastic process (a collection of random variables indexed by time or space), such that every finite collection of those random variables has a multivariate normal distribution. The distribution of a Gaussian process is the joint distribution of all those (infinitely many) random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space. The concept of Gaussian processes is named after Carl Friedrich Gauss because it is based on the notion of the Gaussian distribution (normal distribution). Gaussian processes can be seen as an infinite-dimensional generalization of multivariate normal distributions. Gaussian processes are useful in statistical modelling, benefiting from properties inherited from the normal distribution. For example, if a random process is modelled as a Gaussian process, the distributions of various derived quantities can be obtained explicitly. Such quanti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convergence Of Random Variables
In probability theory, there exist several different notions of convergence of sequences of random variables, including ''convergence in probability'', ''convergence in distribution'', and ''almost sure convergence''. The different notions of convergence capture different properties about the sequence, with some notions of convergence being stronger than others. For example, convergence in distribution tells us about the limit distribution of a sequence of random variables. This is a weaker notion than convergence in probability, which tells us about the value a random variable will take, rather than just the distribution. The concept is important in probability theory, and its applications to statistics and stochastic processes. The same concepts are known in more general mathematics as stochastic convergence and they formalize the idea that certain properties of a sequence of essentially random or unpredictable events can sometimes be expected to settle down into a behavior that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Donsker Classes
A class of functions is considered a Donsker class if it satisfies Donsker's theorem, a functional generalization of the central limit theorem. Definition Let \mathcal be a collection of square integrable functions on a probability space (\mathcal, \mathcal, P) . The empirical process \mathbb_n is the stochastic process on the set \mathcal defined by \mathbb_n(f) = \sqrt(\mathbb_n - P)(f) where \mathbb_n is the empirical measure based on an iid sample X_1, \dots, X_n from P . The class of measurable functions \mathcal is called a Donsker class if the empirical process (\mathbb_n)_^ converges in distribution to a tight Borel measurable element in the space \ell^(\mathcal) . By the central limit theorem, for every finite set of functions f_1, f_2, \dots, f_k \in \mathcal , the random vector (\mathbb_n(f_1), \mathbb_n(f_2), \dots, \mathbb_n(f_k)) converges in distribution to a multivariate normal vector as n \rightarrow \infty . Thus the class \mathcal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Donsker's Theorem
In probability theory, Donsker's theorem (also known as Donsker's invariance principle, or the functional central limit theorem), named after Monroe D. Donsker, is a functional extension of the central limit theorem for empirical distribution functions. Specifically, the theorem states that an appropriately centered and scaled version of the empirical distribution function converges to a Gaussian process. Let X_1, X_2, X_3, \ldots be a sequence of independent and identically distributed (i.i.d.) random variables with mean 0 and variance 1. Let S_n:=\sum_^n X_i. The stochastic process S:=(S_n)_ is known as a random walk. Define the diffusively rescaled random walk (partial-sum process) by : W^(t) := \frac, \qquad t\in ,1 The central limit theorem asserts that W^(1) converges in distribution to a standard Gaussian random variable W(1) as n\to\infty. Donsker's invariance principle extends this convergence to the whole function W^:=(W^(t))_. More precisely, in its modern form, Do ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is f(x) = \frac e^\,. The parameter is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma^2 is the variance. The standard deviation of the distribution is (sigma). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Converges In Distribution
In probability theory, there exist several different notions of convergence of sequences of random variables, including ''convergence in probability'', ''convergence in distribution'', and ''almost sure convergence''. The different notions of convergence capture different properties about the sequence, with some notions of convergence being stronger than others. For example, convergence in distribution tells us about the limit distribution of a sequence of random variables. This is a weaker notion than convergence in probability, which tells us about the value a random variable will take, rather than just the distribution. The concept is important in probability theory, and its applications to statistics and stochastic processes. The same concepts are known in more general mathematics as stochastic convergence and they formalize the idea that certain properties of a sequence of essentially random or unpredictable events can sometimes be expected to settle down into a behavior that i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |