Glivenko–Cantelli Theorem

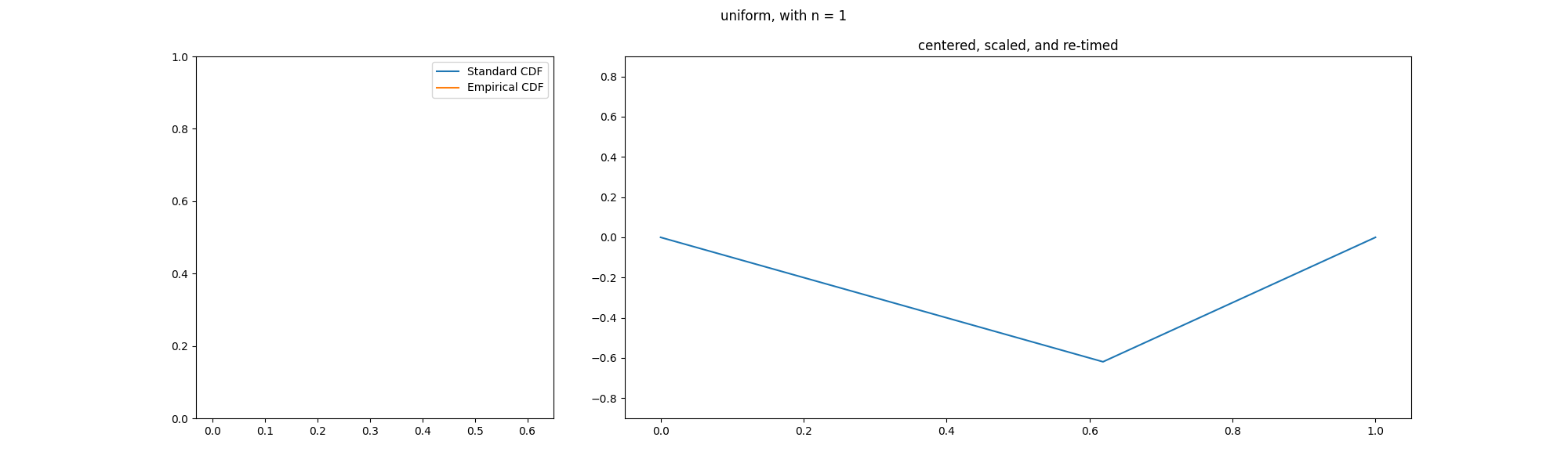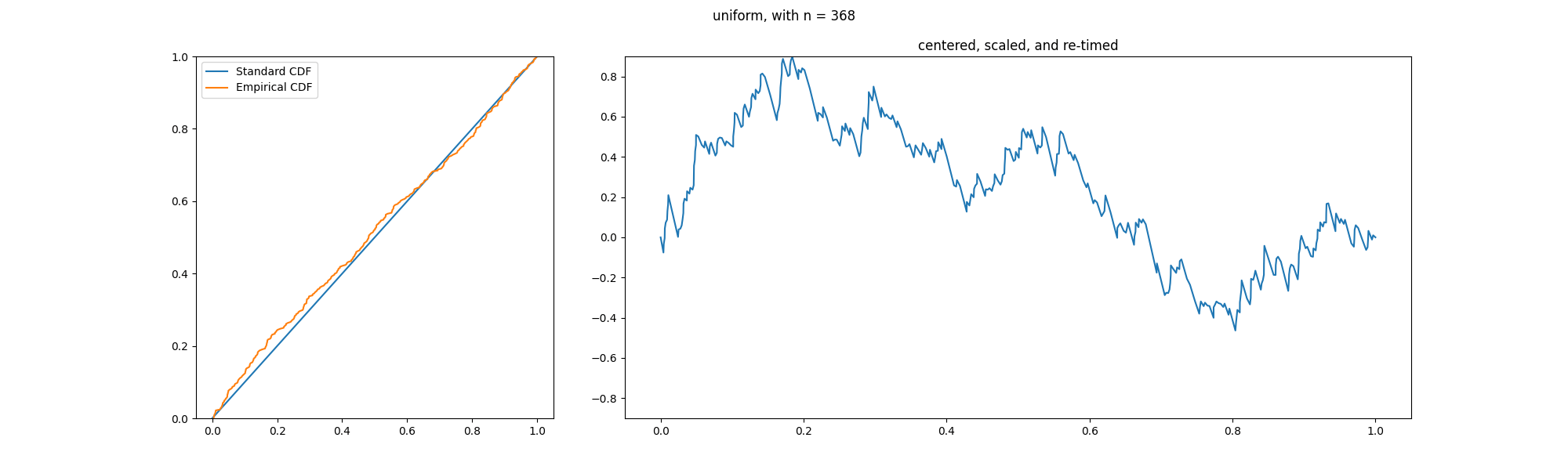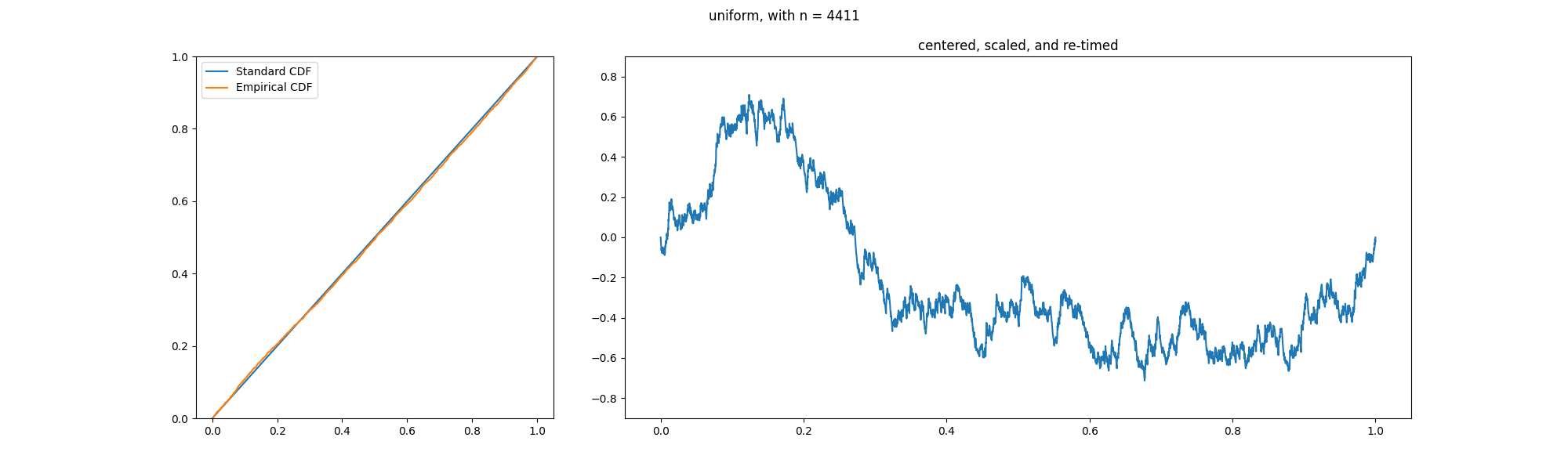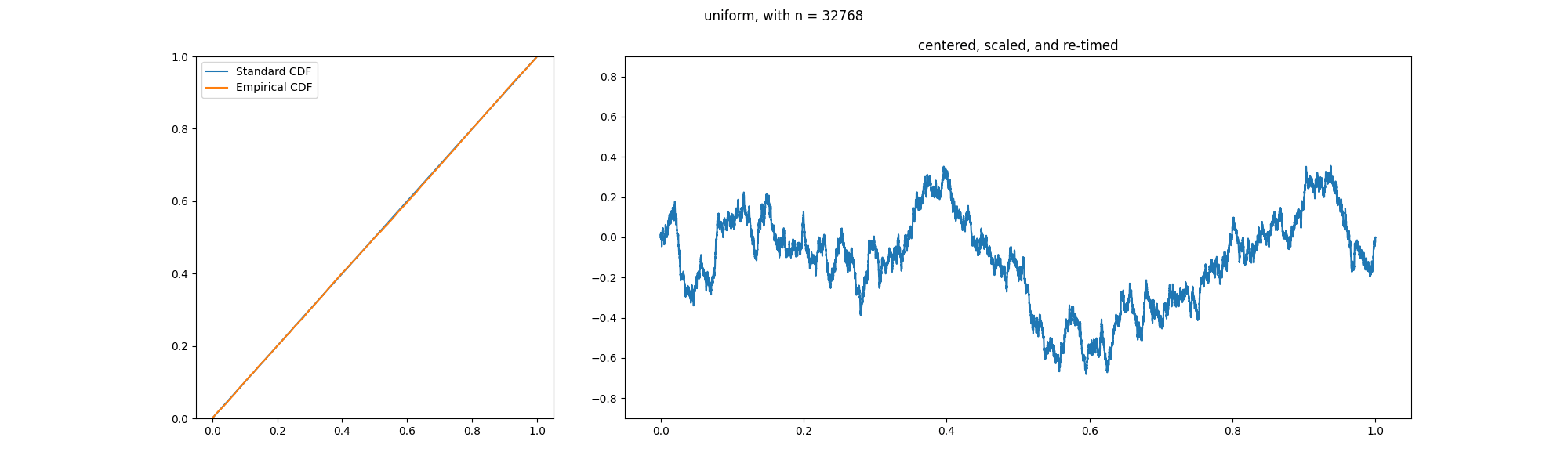
In the theory of probability, the Glivenko–Cantelli theorem (sometimes referred to as the fundamental theorem of statistics), named after Valery Ivanovich Glivenko and Francesco Paolo Cantelli, describes the asymptotic behaviour of the empirical distribution function as the number of independent and identically distributed observations grows. Specifically, the empirical distribution function converges uniformly to the true distribution function almost surely.

The uniform convergence of more general empirical measures becomes an important property of the Glivenko–Cantelli classes of functions or sets. The Glivenko–Cantelli classes arise in Vapnik–Chervonenkis theory, with applications to machine learning. Applications can be found in econometrics making use of M-estimators.

Statement

Assume that $X_1,X_2,\dots$ are independent and identically distributed random variables in $\mathbb$ with common cumulative distribution function $F(x)$. The ''empirical distribution function'' for $X_1,\dots,X_n$ is defined by
$F_n(x) = \frac \sum_^n I_(X_i) = \frac \bigl, \left\\bigr, ,$
where $I_C$ is the indicator function of the set $C.$ For every (fixed) $x,$ $F_n(x)$ is a sequence of random variables which converge to $F(x)$ almost surely by the strong law of large numbers. Glivenko and Cantelli strengthened this result by proving uniform convergence of $F_n$ to $F.$

Theorem

: $\, F_n - F\, _\infty = \sup_ \bigl, F_n(x) - F(x)\bigr, \longrightarrow 0$ almost surely.

This theorem originates with Valery Glivenko and Francesco Cantelli, in 1933.

Remarks

* If $X_n$ is a stationary ergodic process, then $F_n(x)$ converges almost surely to F(x) = \operatorname\mathbb \bigl 1_ \bigr The Glivenko–Cantelli theorem gives a stronger mode of convergence than this in the iid case.
* An even stronger uniform convergence result for the empirical distribution function is available in the form of an extended type of law of the iterated logarithm. See asymptotic properties of the empirical distribution function for this and related results.

Proof

For simplicity, consider a case of continuous random variable $X$. Fix -\infty =x_0 such that $F(x_j)-F(x_)=\frac$ for $j=1,\dots,m$. Now for all $x \in \mathbb$ there exists $j \in \$ such that x \in _,x_j/math>.

: $\begin F_n(x)-F(x) &\leq F_n(x_j)-F(x_) = F_n(x_j)-F(x_j)+\frac1m,\\ F_n(x)-F(x) &\geq F_n(x_)-F(x_j) = F_n(x_)-F(x_)-\frac1m. \end$

Therefore,

: $\, F_n-F\, _\infty = \sup_, F_n(x)-F(x), \leq \max_ , F_n(x_j)-F(x_j), + \frac1m.$

Since $\max_ , F_n(x_j)-F(x_j), \to 0 \text$ by strong law of large numbers, we can guarantee that for any positive $\varepsilon$ and any integer $m$ such that $1/m<\varepsilon$, we can find $N$ such that for all $n \geq N$, we have $\max_ , F_n(x_j)-F(x_j), \leq \varepsilon-1/m \text$. Combined with the above result, this further implies that $\, F_n-F\, _\infty \leq \varepsilon \text$, which is the definition of almost sure convergence.

Empirical measures

One can generalize the ''empirical distribution function'' by replacing the set $(-\infty,x]$ by an arbitrary set ''C'' from a class of sets $\mathcal$ to obtain an empirical measure indexed by sets $C \in \mathcal.$

:$P_n(C)=\frac \sum_^n I_C(X_i), C\in\mathcal$
Where $I_C(x)$ is the indicator function of each set $C$.

Further generalization is the map induced by $P_n$ on measurable real-valued functions ''f'', which is given by

:$f\mapsto P_nf=\int_Sf \, dP_n = \frac 1 n \sum_^n f(X_i), f\in\mathcal.$

Then it becomes an important property of these classes whether the strong law of large numbers holds uniformly on $\mathcal$ or $\mathcal$.

Glivenko–Cantelli class

Consider a set $\ \mathcal\$ with a sigma algebra of Borel set, Borel subsets and a probability measure $\ \mathbb ~.$ For a class of subsets,

:$\mathcal \subset \bigl\$

and a class of functions

:$\mathcal \subset \bigl\$

define random variables

:$\bigl\, \mathbb_n - \mathbb \bigr\, _ = \sup_ \bigl, \mathbb_n(C) - \mathbb(C) \bigr,$

:$\bigl\, \mathbb_n - \mathbb \bigr\, _ = \sup_ \bigl, \mathbb_n f - \mathbb f \bigr,$

where $\ \mathbb_n(C)\$ is the empirical measure, $\ \mathbb_n f\$ is the corresponding map, and

:$\ \mathbb f = \int_\mathcal f \ \mathrm\mathbb\ ,$ assuming that it exists.

Definitions
* A class $\ \mathcal C\$ is called a ''Glivenko–Cantelli class'' (or ''GC class'', or sometimes ''strong GC class'') with respect to a probability measure if
::$\ \bigl\, \mathbb_n - \mathbb \bigr\, _\mathcal \to 0\$ almost surely as $\ n \to \infty ~.$

* A class $\ \mathcal C\$ is a ''weak Glivenko-Cantelli class'' with respect to if it instead satisfies the weaker condition
::$\ \bigl\, \mathbb_n - \mathbb \bigr\, _\mathcal \to 0\$ in probability as $\ n \to \infty ~.$

*A class is called a ''universal Glivenko–Cantelli class'' if it is a GC class with respect to any probability measure $\mathbb$ on $(\mathcal, A)$.

*A class is a ''weak uniform Glivenko–Cantelli class'' if the convergence occurs uniformly over all probability measures $\mathbb$ on $(\mathcal, A)$: For every $\varepsilon > 0$,
::$\ \sup_ \Pr\left(\bigl\, \mathbb_n - \mathbb \bigr\, _\mathcal > \varepsilon\right) \to 0\$ as $\ n \to \infty ~.$
*A class is a (strong) ''uniform Glivenko-Cantelli class'' if it satisfies the stronger condition that for every $\varepsilon > 0$,
::$\ \sup_ \Pr\left(\sup_ \bigl\, \mathbb_m - \mathbb \bigr\, _\mathcal > \varepsilon\right) \to 0\$ as $\ n \to \infty ~.$

Glivenko–Cantelli classes of functions (as well as their uniform and universal forms) are defined similarly, replacing all instances of $\mathcal$ with $\mathcal$.

The weak and strong versions of the various Glivenko-Cantelli properties often coincide under certain regularity conditions. The following definition commonly appears in such regularity conditions:

* A class of functions $\mathcal$ is ''image-admissible Suslin'' if there exists a Suslin space $\Omega$ and a surjection $T:\Omega \rightarrow \mathcal$ such that the map (x, y) \mapsto (y)x) is measurable $\mathcal\times\Omega$.

* A class of measurable sets $\mathcal$ is image-admissible Suslin if the class of functions $\$ is image-admissible Suslin, where $\mathbf_C$ denotes the indicator function for the set $C$.

Theorems

The following two theorems give sufficient conditions for the weak and strong versions of the Glivenko-Cantelli property to be equivalent.

Theorem ( Talagrand, 1987)
: ''Let $\mathcal$ be a class of functions that is integrable $\mathbb$, and define $\mathcal_0 = \$. Then the following are equivalent:''
* ''$\mathcal$ is a weak Glivenko-Cantelli class and $\mathcal_0$ is dominated by an integrable function''
* ''$\mathcal$ is a Glivenko-Cantelli class''

Theorem (Dudley, Giné, and Zinn, 1991)
: ''Suppose that a function class $\mathcal$ is bounded. Also suppose that the set $\mathcal_0 = \$ is image-admissible Suslin. Then $\mathcal$ is a weak uniform Glivenko-Cantelli class if and only if it is a strong uniform Glivenko-Cantelli class.''

The following theorem is central to statistical learning of binary classification tasks.

Theorem (Vapnik and Chervonenkis, 1968)
: ''Under certain consistency conditions, a universally measurable class of sets $\ \mathcal\$ is a uniform Glivenko-Cantelli class if and only if it is a Vapnik–Chervonenkis class.''

There exist a variety of consistency conditions for the equivalence of uniform Glivenko-Cantelli and Vapnik-Chervonenkis classes. In particular, either of the following conditions for a class $\mathcal$ suffice:
* $\mathcal$ is image-admissible Suslin.
* $\mathcal$ is universally separable: There exists a countable subset $\mathcal$ of $\mathcal$ such that each set $C\in\mathcal$ can be written as the pointwise limit of sets in $\mathcal_0$.

Examples

* Let $S=\mathbb R$ and $=\$. The classical Glivenko–Cantelli theorem implies that this class is a universal GC class. Furthermore, by Kolmogorov's theorem,
:$\sup_\, P_n-P\, _ \sim n^$, that is $\mathcal$ is uniformly Glivenko–Cantelli class.

* Let ''P'' be a nonatomic probability measure on ''S'' and $\mathcal$ be a class of all finite subsets in ''S''. Because $A_n=\\in \mathcal$, $P(A_n)=0$, $P_n(A_n)=1$, we have that $\, P_n-P\, _=1$ and so $\mathcal$ is ''not'' a GC class with respect to ''P''.

See also

* Donsker's theorem
* Dvoretzky–Kiefer–Wolfowitz inequality – strengthens the Glivenko–Cantelli theorem by quantifying the rate of convergence.

References

Further reading

*
*
*
*
*
*

{{DEFAULTSORT:Glivenko-Cantelli Theorem
Empirical process
Asymptotic theory (statistics)
Theorems in probability theory
Theorems in statistics