|
Differential Item Functioning
Differential item functioning (DIF) is a statistical property of a test item that indicates how likely it is for individuals from distinct groups, possessing similar abilities, to respond differently to the item. It manifests when individuals from different groups, with comparable skill levels, do not have an equal likelihood of answering a question correctly. There are two primary types of DIF: uniform DIF, where one group consistently has an advantage over the other, and nonuniform DIF, where the advantage varies based on the individual's ability level. The presence of DIF requires review and judgment, but it doesn't always signify bias. DIF analysis provides an indication of unexpected behavior of items on a test. DIF characteristic of an item isn't solely determined by varying probabilities of selecting a specific response among individuals from different groups. Rather, DIF becomes pronounced when individuals from different groups, who possess the ''same underlying true ability' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Test Item
Questionnaire construction refers to the design of a questionnaire to gather statistically useful information about a given topic. When properly constructed and responsibly administered, questionnaires can provide valuable data about any given subject. Questionnaires Questionnaires are frequently used in quantitative marketing research and social research. They are a valuable method of collecting a wide range of information from a large number of individuals, often referred to as respondents. What is often referred to as "adequate questionnaire construction" is critical to the success of a survey. Inappropriate questions, incorrect ordering of questions, incorrect scaling, or a bad questionnaire format can make the survey results valueless, as they may not accurately reflect the views and opinions of the participants. Different methods can be useful for checking a questionnaire and making sure it is accurately capturing the intended information. Initial advice may include: * con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
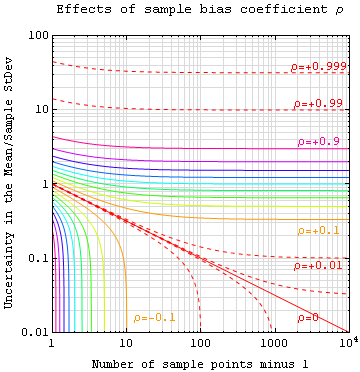
Ratio Estimator
The ratio estimator is a statistical estimator for the ratio of means of two random variables. Ratio estimates are biased and corrections must be made when they are used in experimental or survey work. The ratio estimates are asymmetrical and symmetrical tests such as the t test should not be used to generate confidence intervals. The bias is of the order ''O''(1/''n'') (see big O notation) so as the sample size (''n'') increases, the bias will asymptotically approach 0. Therefore, the estimator is approximately unbiased for large sample sizes. Definition Assume there are two characteristics – ''x'' and ''y'' – that can be observed for each sampled element in the data set. The ratio ''R'' is : R = \bar_y / \bar_x The ratio estimate of a value of the ''y'' variate (''θ''''y'') is : \theta_y = R \theta_x where ''θ''''x'' is the corresponding value of the ''x'' variate. ''θ''''y'' is known to be asymptotically normally distributed.Scott AJ, Wu CFJ (1981) On the asym ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wald Statistic
In statistics, the Wald test (named after Abraham Wald) assesses constraints on statistical parameters based on the weighted distance between the unrestricted estimate and its hypothesized value under the null hypothesis, where the weight is the precision of the estimate. Intuitively, the larger this weighted distance, the less likely it is that the constraint is true. While the finite sample distributions of Wald tests are generally unknown, it has an asymptotic χ2-distribution under the null hypothesis, a fact that can be used to determine statistical significance. Together with the Lagrange multiplier test and the likelihood-ratio test, the Wald test is one of three classical approaches to hypothesis testing. An advantage of the Wald test over the other two is that it only requires the estimation of the unrestricted model, which lowers the computational burden as compared to the likelihood-ratio test. However, a major disadvantage is that (in finite samples) it is not i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Error
The standard error (SE) of a statistic (usually an estimator of a parameter, like the average or mean) is the standard deviation of its sampling distribution or an estimate of that standard deviation. In other words, it is the standard deviation of statistic values (each value is per sample that is a set of observations made per sampling on the same population). If the statistic is the sample mean, it is called the standard error of the mean (SEM). The standard error is a key ingredient in producing confidence intervals. The sampling distribution of a mean is generated by repeated sampling from the same population and recording the sample mean per sample. This forms a distribution of different means, and this distribution has its own mean and variance. Mathematically, the variance of the sampling mean distribution obtained is equal to the variance of the population divided by the sample size. This is because as the sample size increases, sample means cluster more closely arou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
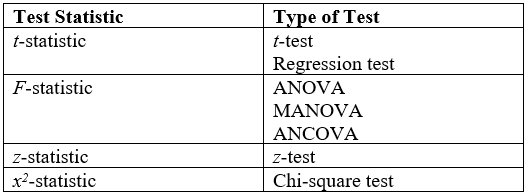
Test Statistic
Test statistic is a quantity derived from the sample for statistical hypothesis testing.Berger, R. L.; Casella, G. (2001). ''Statistical Inference'', Duxbury Press, Second Edition (p.374) A hypothesis test is typically specified in terms of a test statistic, considered as a numerical summary of a data-set that reduces the data to one value that can be used to perform the hypothesis test. In general, a test statistic is selected or defined in such a way as to quantify, within observed data, behaviours that would distinguish the null from the alternative hypothesis, where such an alternative is prescribed, or that would characterize the null hypothesis if there is no explicitly stated alternative hypothesis. An important property of a test statistic is that its sampling distribution under the null hypothesis must be calculable, either exactly or approximately, which allows ''p''-values to be calculated. A ''test statistic'' shares some of the same qualities of a descriptive stat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normally Distributed
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real number, real-valued random variable. The general form of its probability density function is f(x) = \frac e^\,. The parameter is the Mean#Mean of a probability distribution, mean or expected value, expectation of the distribution (and also its median and mode (statistics), mode), while the parameter \sigma^2 is the variance. The standard deviation of the distribution is (sigma). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural science, natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Significance
In statistical hypothesis testing, a result has statistical significance when a result at least as "extreme" would be very infrequent if the null hypothesis were true. More precisely, a study's defined significance level, denoted by \alpha, is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true; and the p-value, ''p''-value of a result, ''p'', is the probability of obtaining a result at least as extreme, given that the null hypothesis is true. The result is said to be ''statistically significant'', by the standards of the study, when p \le \alpha. The significance level for a study is chosen before data collection, and is typically set to 5% or much lower—depending on the field of study. In any experiment or Observational study, observation that involves drawing a Sampling (statistics), sample from a Statistical population, population, there is always the possibility that an observed effect would have occurred due to sampling error al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Student's T-test
Student's ''t''-test is a statistical test used to test whether the difference between the response of two groups is statistically significant or not. It is any statistical hypothesis test in which the test statistic follows a Student's ''t''-distribution under the null hypothesis. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known (typically, the scaling term is unknown and is therefore a nuisance parameter). When the scaling term is estimated based on the data, the test statistic—under certain conditions—follows a Student's ''t'' distribution. The ''t''-test's most common application is to test whether the means of two populations are significantly different. In many cases, a ''Z''-test will yield very similar results to a ''t''-test because the latter converges to the former as the size of the dataset increases. History The term "''t''-statistic" is abbreviated from " ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptote
In analytic geometry, an asymptote () of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the ''x'' or ''y'' coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity. The word asymptote is derived from the Greek ἀσύμπτωτος (''asumptōtos'') which means "not falling together", from ἀ priv. + σύν "together" + πτωτ-ός "fallen". The term was introduced by Apollonius of Perga in his work on conic sections, but in contrast to its modern meaning, he used it to mean any line that does not intersect the given curve. There are three kinds of asymptotes: ''horizontal'', ''vertical'' and ''oblique''. For curves given by the graph of a function , horizontal asymptotes are horizontal lines that the graph of the function approaches as ''x'' tends to Vertical asymptotes are vertical lines near which the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Slope
In mathematics, the slope or gradient of a Line (mathematics), line is a number that describes the direction (geometry), direction of the line on a plane (geometry), plane. Often denoted by the letter ''m'', slope is calculated as the ratio of the vertical change to the horizontal change ("rise over run") between two distinct points on the line, giving the same number for any choice of points. The line may be physical – as set by a Surveying, road surveyor, pictorial as in a diagram of a road or roof, or Pure mathematics, abstract. An application of the mathematical concept is found in the grade (slope), grade or gradient in geography and civil engineering. The ''steepness'', incline, or grade of a line is the absolute value of its slope: greater absolute value indicates a steeper line. The line trend is defined as follows: *An "increasing" or "ascending" line goes from left to right and has positive slope: m>0. *A "decreasing" or "descending" line goes from left to right ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inflection Point
In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (rarely inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case of the graph of a function, it is a point where the function changes from being concave (concave downward) to convex (concave upward), or vice versa. For the graph of a function of differentiability class (its first derivative , and its second derivative , exist and are continuous), the condition can also be used to find an inflection point since a point of must be passed to change from a positive value (concave upward) to a negative value (concave downward) or vice versa as is continuous; an inflection point of the curve is where and changes its sign at the point (from positive to negative or from negative to positive). A point where the second derivative vanishes but does not change its sign is sometimes called a point of undulation or und ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logistic Function
A logistic function or logistic curve is a common S-shaped curve ( sigmoid curve) with the equation f(x) = \frac where The logistic function has domain the real numbers, the limit as x \to -\infty is 0, and the limit as x \to +\infty is L. The exponential function with negated argument (e^ ) is used to define the standard logistic function, depicted at right, where L=1, k=1, x_0=0, which has the equation f(x) = \frac and is sometimes simply called the sigmoid. It is also sometimes called the expit, being the inverse function of the logit. The logistic function finds applications in a range of fields, including biology (especially ecology), biomathematics, chemistry, demography, economics, geoscience, mathematical psychology, probability, sociology, political science, linguistics, statistics, and artificial neural networks. There are various generalizations, depending on the field. History The logistic function was introduced in a series of three papers by Pier ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |