|
Data Transformation (statistics)
In statistics, data transformation is the application of a deterministic mathematical function to each point in a data set—that is, each data point ''zi'' is replaced with the transformed value ''yi'' = ''f''(''zi''), where ''f'' is a function. Transforms are usually applied so that the data appear to more closely meet the assumptions of a statistical inference procedure that is to be applied, or to improve the interpretability or appearance of graphs. Nearly always, the function that is used to transform the data is invertible, and generally is continuous. The transformation is usually applied to a collection of comparable measurements. For example, if we are working with data on peoples' incomes in some currency unit, it would be common to transform each person's income value by the logarithm function. Motivation Guidance for how data should be transformed, or whether a transformation should be applied at all, should come from the particular statistical analysis to be pe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Population Vs Area
Population is a set of humans or other organisms in a given region or area. Governments conduct a census to quantify the resident population size within a given jurisdiction. The term is also applied to non-human animals, microorganisms, and plants, and has specific uses within such fields as ecology and genetics. Etymology The word ''population'' is derived from the Late Latin ''populatio'' (a people, a multitude), which itself is derived from the Latin word ''populus'' (a people). Use of the term Social sciences In sociology and population geography, population refers to a group of human beings with some predefined feature in common, such as location, race, ethnicity, nationality, or religion. Ecology In ecology, a population is a group of organisms of the same species which inhabit the same geographical area and are capable of interbreeding. The area of a sexual population is the area where interbreeding is possible between any opposite-sex pair within the area ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Population
In statistics, a population is a set of similar items or events which is of interest for some question or experiment. A statistical population can be a group of existing objects (e.g. the set of all stars within the Milky Way galaxy) or a hypothetical and potentially infinite group of objects conceived as a generalization from experience (e.g. the set of all possible hands in a game of poker). A population with finitely many values N in the support of the population distribution is a finite population with population size N. A population with infinitely many values in the support is called infinite population. A common aim of statistical analysis is to produce information about some chosen population. In statistical inference, a subset of the population (a statistical '' sample'') is chosen to represent the population in a statistical analysis. Moreover, the statistical sample must be unbiased and accurately model the population. The ratio of the size of this statistical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, unlike the standard deviation, its units differ from the random variable, which is why the standard devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
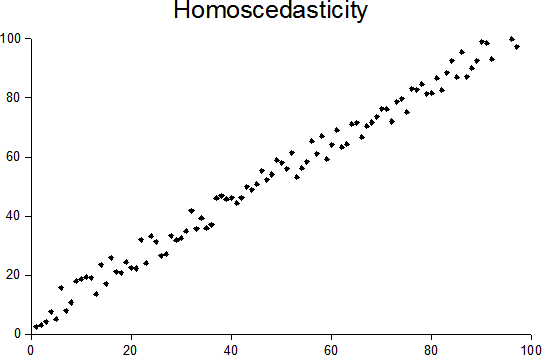
Homoscedasticity
In statistics, a sequence of random variables is homoscedastic () if all its random variables have the same finite variance; this is also known as homogeneity of variance. The complementary notion is called heteroscedasticity, also known as heterogeneity of variance. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. “Skedasticity” comes from the Ancient Greek word “skedánnymi”, meaning “to scatter”. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in Biased estimator, unbiased but Efficiency (statistics), inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson product-moment correlation coefficient, Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical hypothesis testing, statistical tests ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial Regression
In statistics, polynomial regression is a form of regression analysis in which the relationship between the independent variable ''x'' and the dependent variable ''y'' is modeled as a polynomial in ''x''. Polynomial regression fits a nonlinear relationship between the value of ''x'' and the corresponding conditional mean of ''y'', denoted E(''y'' , ''x''). Although polynomial regression fits a nonlinear model to the data, as a statistical estimation problem it is linear, in the sense that the regression function E(''y'' , ''x'') is linear in the unknown parameters that are estimated from the data. Thus, polynomial regression is a special case of linear regression. The explanatory (independent) variables resulting from the polynomial expansion of the "baseline" variables are known as higher-degree terms. Such variables are also used in classification settings. History Polynomial regression models are usually fit using the method of least squares. The leas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dependent And Independent Variables
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, on the other hand, are not seen as depending on any other variable in the scope of the experiment in question. Rather, they are controlled by the experimenter. In pure mathematics In mathematics, a function (mathematics), function is a rule for taking an input (in the simplest case, a number or set of numbers)Carlson, Robert. A concrete introduction to real analysis. CRC Press, 2006. p.183 and providing an output (which may also be a number). A symbol that stands for an arbitrary input is called an independent variable, while a symbol that stands for an arbitrary output is called a dependent variable. The most common symbol for the input is , and the most common symbol for the o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear
In mathematics, the term ''linear'' is used in two distinct senses for two different properties: * linearity of a '' function'' (or '' mapping''); * linearity of a '' polynomial''. An example of a linear function is the function defined by f(x)=(ax,bx) that maps the real line to a line in the Euclidean plane R2 that passes through the origin. An example of a linear polynomial in the variables X, Y and Z is aX+bY+cZ+d. Linearity of a mapping is closely related to '' proportionality''. Examples in physics include the linear relationship of voltage and current in an electrical conductor ( Ohm's law), and the relationship of mass and weight. By contrast, more complicated relationships, such as between velocity and kinetic energy, are '' nonlinear''. Generalized for functions in more than one dimension, linearity means the property of a function of being compatible with addition and scaling, also known as the superposition principle. Linearity of a polynomial means that its de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Regression
In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A model with exactly one explanatory variable is a ''simple linear regression''; a model with two or more explanatory variables is a multiple linear regression. This term is distinct from multivariate linear regression, which predicts multiple correlated dependent variables rather than a single dependent variable. In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters are estimation theory, estimated from the data. Most commonly, the conditional mean of the response given the values of the explanatory variables (or predictors) is assumed to be an affine function of those values; less commonly, the conditional median or some other quantile is used. Like all forms of regression analysis, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplicative Inverse
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when Multiplication, multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a rational number, fraction ''a''/''b'' is ''b''/''a''. For the multiplicative inverse of a real number, divide 1 by the number. For example, the reciprocal of 5 is one fifth (1/5 or 0.2), and the reciprocal of 0.25 is 1 divided by 0.25, or 4. The reciprocal function, the Function (mathematics), function ''f''(''x'') that maps ''x'' to 1/''x'', is one of the simplest examples of a function which is its own inverse (an Involution (mathematics), involution). Multiplying by a number is the same as Division (mathematics), dividing by its reciprocal and vice versa. For example, multiplication by 4/5 (or 0.8) will give the same result as division by 5/4 (or 1.25). Therefore, multiplication by a number followed by multiplication by its reciprocal yie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |