|
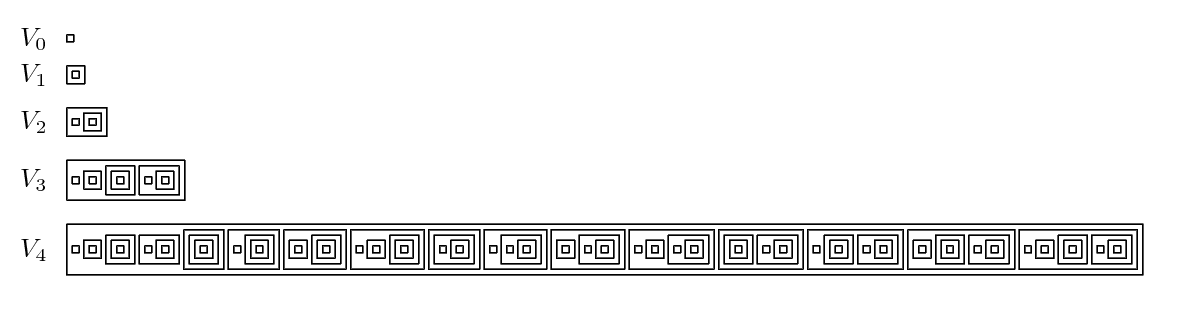
Beth Two
In mathematics, particularly in set theory, the beth numbers are a certain sequence of infinite cardinal numbers (also known as transfinite numbers), conventionally written \beth_0, \beth_1, \beth_2, \beth_3, \dots, where \beth is the Hebrew letter beth. The beth numbers are related to the aleph numbers (\aleph_0, \aleph_1, \dots), but unless the generalized continuum hypothesis is true, there are numbers indexed by \aleph that are not indexed by \beth or the gimel function \gimel. Definition Beth numbers are defined by transfinite recursion: * \beth_0 = \aleph_0, * \beth_ = 2^, * \beth_\lambda = \sup\Bigl\, where \alpha is an ordinal and \lambda is a limit ordinal. The cardinal \beth_0 = \aleph_0 is the cardinality of any countably infinite set such as the set \mathbb of natural numbers, so that \beth_0 = , \mathbb, . Let \alpha be an ordinal, and A_\alpha be a set with cardinality \beth_\alpha = , A_\alpha, . Then, * \mathcal(A_\alpha) denotes the power set of A_\al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardinal Exponentiation
In mathematics, a cardinal number, or cardinal for short, is what is commonly called the number of elements of a set. In the case of a finite set, its cardinal number, or cardinality is therefore a natural number. For dealing with the case of infinite sets, the infinite cardinal numbers have been introduced, which are often denoted with the Hebrew letter \aleph (aleph) marked with subscript indicating their rank among the infinite cardinals. Cardinality is defined in terms of bijective functions. Two sets have the same cardinality if, and only if, there is a one-to-one correspondence (bijection) between the elements of the two sets. In the case of finite sets, this agrees with the intuitive notion of number of elements. In the case of infinite sets, the behavior is more complex. A fundamental theorem due to Georg Cantor shows that it is possible for two infinite sets to have different cardinalities, and in particular the cardinality of the set of real numbers is greate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for example, The set of all rational numbers is often referred to as "the rationals", and is closed under addition, subtraction, multiplication, and division by a nonzero rational number. It is a field under these operations and therefore also called the field of rationals or the field of rational numbers. It is usually denoted by boldface , or blackboard bold A rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits (example: ), or eventually begins to repeat the same finite sequence of digits over and over (example: ). This statement is true not only in base 10, but also in every other integer base, such as the binary and hexadecimal ones (see ). A real n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aleph Null
In mathematics, particularly in set theory, the aleph numbers are a sequence of numbers used to represent the cardinality (or size) of infinite sets. They were introduced by the mathematician Georg Cantor and are named after the symbol he used to denote them, the Hebrew letter aleph (ℵ). The smallest cardinality of an infinite set is that of the natural numbers, denoted by \aleph_0 (read ''aleph-nought'', ''aleph-zero'', or ''aleph-null''); the next larger cardinality of a well-ordered set is \aleph_1, then \aleph_2, then \aleph_3, and so on. Continuing in this manner, it is possible to define an infinite cardinal number \aleph_ for every ordinal number \alpha, as described below. The concept and notation are due to Georg Cantor, who defined the notion of cardinality and realized that infinite sets can have different cardinalities. The aleph numbers differ from the infinity (\infty) commonly found in algebra and calculus, in that the alephs measure the sizes of sets, while ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuum Hypothesis
In mathematics, specifically set theory, the continuum hypothesis (abbreviated CH) is a hypothesis about the possible sizes of infinite sets. It states: Or equivalently: In Zermelo–Fraenkel set theory with the axiom of choice (ZFC), this is equivalent to the following equation in aleph numbers: 2^=\aleph_1, or even shorter with beth numbers: \beth_1 = \aleph_1. The continuum hypothesis was advanced by Georg Cantor in 1878, and establishing its truth or falsehood is the first of Hilbert's 23 problems presented in 1900. The answer to this problem is independent of ZFC, so that either the continuum hypothesis or its negation can be added as an axiom to ZFC set theory, with the resulting theory being consistent if and only if ZFC is consistent. This independence was proved in 1963 by Paul Cohen, complementing earlier work by Kurt Gödel in 1940. The name of the hypothesis comes from the term '' continuum'' for the real numbers. History Cantor believed the continuum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transfinite Induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for example to sets of ordinal numbers or cardinal numbers. Its correctness is a theorem of ZFC. Induction by cases Let P(\alpha) be a property defined for all ordinals \alpha. Suppose that whenever P(\beta) is true for all \beta < \alpha, then is also true. Then transfinite induction tells us that is true for all ordinals. Usually the proof is broken down into three cases: * Zero case: Prove that is true. * Successor case: Prove that for any successor ordinal , follows from (and, if necessary, for all ). * Limit case: Prove that for any [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Order
In mathematics, a total order or linear order is a partial order in which any two elements are comparable. That is, a total order is a binary relation \leq on some set X, which satisfies the following for all a, b and c in X: # a \leq a ( reflexive). # If a \leq b and b \leq c then a \leq c ( transitive). # If a \leq b and b \leq a then a = b ( antisymmetric). # a \leq b or b \leq a ( strongly connected, formerly called totality). Requirements 1. to 3. just make up the definition of a partial order. Reflexivity (1.) already follows from strong connectedness (4.), but is required explicitly by many authors nevertheless, to indicate the kinship to partial orders. Total orders are sometimes also called simple, connex, or full orders. A set equipped with a total order is a totally ordered set; the terms simply ordered set, linearly ordered set, toset and loset are also used. The term ''chain'' is sometimes defined as a synonym of ''totally ordered set'', but generally refers to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axiom Of Choice
In mathematics, the axiom of choice, abbreviated AC or AoC, is an axiom of set theory. Informally put, the axiom of choice says that given any collection of non-empty sets, it is possible to construct a new set by choosing one element from each set, even if the collection is infinite. Formally, it states that for every indexed family (S_i)_ of nonempty sets (S_i as a nonempty set indexed with i), there exists an indexed set (x_i)_ such that x_i \in S_i for every i \in I. The axiom of choice was formulated in 1904 by Ernst Zermelo in order to formalize his proof of the well-ordering theorem. The axiom of choice is equivalent to the statement that every partition has a transversal. In many cases, a set created by choosing elements can be made without invoking the axiom of choice, particularly if the number of sets from which to choose the elements is finite, or if a canonical rule on how to choose the elements is available — some distinguishing property that happens to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Neumann Universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted by ''V'', is the class of hereditary well-founded sets. This collection, which is formalized by Zermelo–Fraenkel set theory (ZFC), is often used to provide an interpretation or motivation of the axioms of ZFC. The concept is named after John von Neumann, although it was first published by Ernst Zermelo in 1930. The rank of a well-founded set is defined inductively as the smallest ordinal number greater than the ranks of all members of the set. In particular, the rank of the empty set is zero, and every ordinal has a rank equal to itself. The sets in ''V'' are divided into the transfinite hierarchy ''Vα'', called the cumulative hierarchy, based on their rank. Definition The cumulative hierarchy is a collection of sets ''V''α indexed by the class of ordinal numbers; in particular, ''V''α is the set of all sets having ranks less than α. Thus there is one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Continuum Hypothesis
In mathematics, specifically set theory, the continuum hypothesis (abbreviated CH) is a hypothesis about the possible sizes of infinite sets. It states: Or equivalently: In Zermelo–Fraenkel set theory with the axiom of choice (ZFC), this is equivalent to the following equation in aleph numbers: 2^=\aleph_1, or even shorter with beth numbers: \beth_1 = \aleph_1. The continuum hypothesis was advanced by Georg Cantor in 1878, and establishing its truth or falsehood is the first of Hilbert's 23 problems presented in 1900. The answer to this problem is independent of ZFC, so that either the continuum hypothesis or its negation can be added as an axiom to ZFC set theory, with the resulting theory being consistent if and only if ZFC is consistent. This independence was proved in 1963 by Paul Cohen, complementing earlier work by Kurt Gödel in 1940. The name of the hypothesis comes from the term '' continuum'' for the real numbers. History Cantor believed the continuum hy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supremum
In mathematics, the infimum (abbreviated inf; : infima) of a subset S of a partially ordered set P is the greatest element in P that is less than or equal to each element of S, if such an element exists. If the infimum of S exists, it is unique, and if ''b'' is a lower bound of S, then ''b'' is less than or equal to the infimum of S. Consequently, the term ''greatest lower bound'' (abbreviated as ) is also commonly used. The supremum (abbreviated sup; : suprema) of a subset S of a partially ordered set P is the least element in P that is greater than or equal to each element of S, if such an element exists. If the supremum of S exists, it is unique, and if ''b'' is an upper bound of S, then the supremum of S is less than or equal to ''b''. Consequently, the supremum is also referred to as the ''least upper bound'' (or ). The infimum is, in a precise sense, dual to the concept of a supremum. Infima and suprema of real numbers are common special cases that are important in analy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |