|
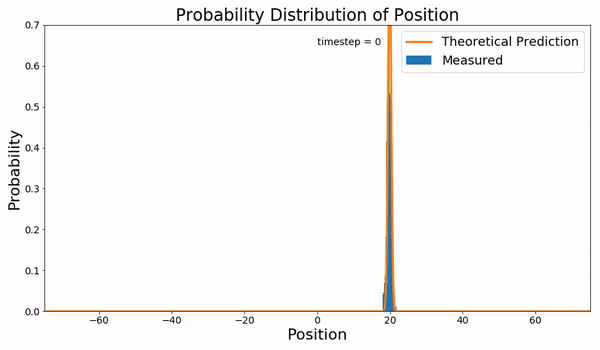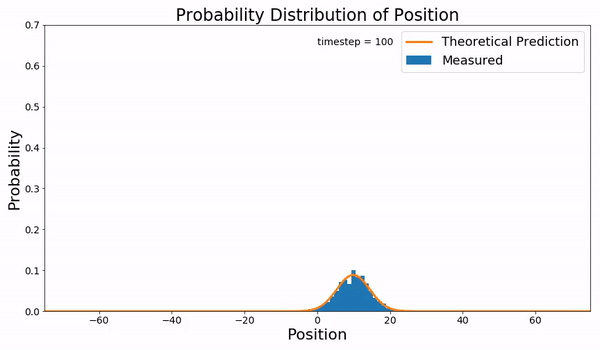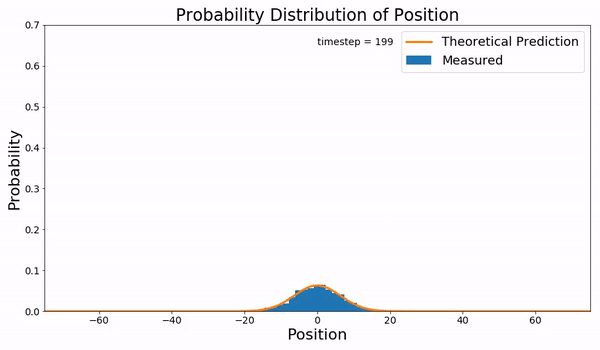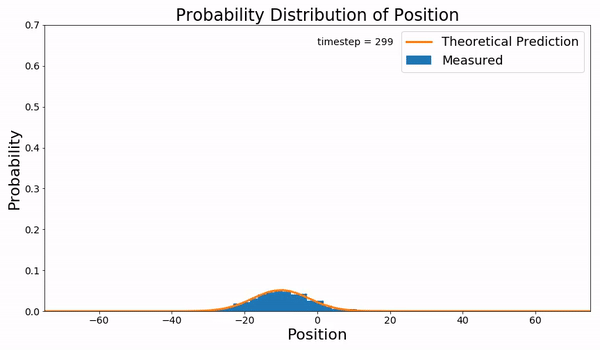
Wiener Process
In mathematics, the Wiener process (or Brownian motion, due to its historical connection with Brownian motion, the physical process of the same name) is a real-valued continuous-time stochastic process discovered by Norbert Wiener. It is one of the best known Lévy processes (càdlàg stochastic processes with stationary increments, stationary independent increments). It occurs frequently in pure and applied mathematics, economy, economics, quantitative finance, evolutionary biology, and physics. The Wiener process plays an important role in both pure and applied mathematics. In pure mathematics, the Wiener process gave rise to the study of continuous time martingale (probability theory), martingales. It is a key process in terms of which more complicated stochastic processes can be described. As such, it plays a vital role in stochastic calculus, diffusion processes and even potential theory. It is the driving process of Schramm–Loewner evolution. In applied mathematics, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wiener Process Zoom
Wiener (from German: "wikt:Viennese, Viennese") may refer to: Food * A Vienna sausage of German origin, in German ''Wiener'', named after the capital of Austria * A hot dog, a cooked sausage, traditionally grilled or steamed and served in a sliced bun * A Polish sausage (kielbasa) or "wenar" People * Wiener (surname) Places *Wiener Neudorf, a town in the eastern part of the Mödling district, Austria *Wiener Neustadt, a town south of Vienna, in the state of Lower Austria, Austria *Wiener Stadthalle, an indoor arena, in Vienna, Austria *Wiener Staatsoper, the Vienna State Opera Other uses *The Wiener AC, also known as Wiener AC or WAC, an Austrian sports club in Vienna * Wiener process, a mathematical model related to Brownian motion * Wiener equation, named after Norbert Wiener, assumes the current velocity of a fluid particle fluctuates randomly * Wiener filter, a noise filter used in signal processing * Wiener (crater), a crater on the far side of the Moon *''Wiener Bonbons' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Calculus
Stochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes. This field was created and started by the Japanese people, Japanese mathematician Kiyosi Itô during World War II. The best-known stochastic process to which stochastic calculus is applied is the Wiener process (named in honor of Norbert Wiener), which is used for modeling Brownian motion as described by Louis Bachelier in 1900 and by Albert Einstein in 1905 and other physical diffusion processes in space of particles subject to random forces. Since the 1970s, the Wiener process has been widely applied in financial mathematics and economics to model the evolution in time of stock prices and bond interest rates. The main flavours of stochastic calculus are the Itô calculus and its variational relative the Malliavin calculus. For technical reasons the Itô integ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Path Integral Formulation
The path integral formulation is a description in quantum mechanics that generalizes the stationary action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude. This formulation has proven crucial to the subsequent development of theoretical physics, because manifest Lorentz covariance (time and space components of quantities enter equations in the same way) is easier to achieve than in the operator formalism of canonical quantization. Unlike previous methods, the path integral allows one to easily change coordinates between very different canonical descriptions of the same quantum system. Another advantage is that it is in practice easier to guess the correct form of the Lagrangian of a theory, which naturally enters the path integrals (for interactions of a certain type, these ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langevin Equation
In physics, a Langevin equation (named after Paul Langevin) is a stochastic differential equation describing how a system evolves when subjected to a combination of deterministic and fluctuating ("random") forces. The dependent variables in a Langevin equation typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation. One application is to Brownian motion, which models the fluctuating motion of a small particle in a fluid. Brownian motion as a prototype The original Langevin equation describes Brownian motion, the apparently random movement of a particle in a fluid due to collisions with the molecules of the fluid, m\frac=-\lambda \mathbf+\boldsymbol\left( t\right). Here, \mathbf is the velocity of the particle, \lambda is its damping coefficient, and m is its mass. The force acting on the particle is w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fokker–Planck Equation
In statistical mechanics and information theory, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag (physics), drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. The Fokker–Planck equation has multiple applications in information theory, graph theory, data science, finance, economics etc. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. When applied to particle position and momentum distributions, it is known as the Klein–Kr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Theory
Control theory is a field of control engineering and applied mathematics that deals with the control system, control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any ''delay'', ''overshoot'', or ''steady-state error'' and ensuring a level of control Stability theory, stability; often with the aim to achieve a degree of Optimal control, optimality. To do this, a controller with the requisite corrective behavior is required. This controller monitors the controlled process variable (PV), and compares it with the reference or Setpoint (control system), set point (SP). The difference between actual and desired value of the process variable, called the ''error'' signal, or SP-PV error, is applied as feedback to generate a control action to bring the controlled process variable to the same value as the set point. Other aspects ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Filter (signal Processing)
In signal processing, a filter is a device or process that removes some unwanted components or features from a Signal (electronics), signal. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal. Most often, this means removing some frequency, frequencies or frequency bands. However, filters do not exclusively act in the frequency domain; especially in the field of image processing many other targets for filtering exist. Correlations can be removed for certain frequency components and not for others without having to act in the frequency domain. Filters are widely used in electronics and telecommunication, in radio, television, audio recording, radar, control systems, music synthesis, image processing, computer graphics, and structural dynamics. There are many different bases of classifying filters and these overlap in many different ways; there is no simple hierarchical classification. Fil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brownian Noise
In science, Brownian noise, also known as Brown noise or red noise, is the type of signal noise produced by Brownian motion, hence its alternative name of random walk noise. The term "Brown noise" does not come from brown, the color, but after Robert Brown (Scottish botanist from Montrose), Robert Brown, who documented the erratic motion for multiple types of inanimate particles in water. The term "red noise" comes from the "white noise"/"white light" analogy; red noise is strong in longer wavelengths, similar to the red end of the visible spectrum. Explanation The graphic representation of the sound signal mimics a Brownian pattern. Its spectral density is inversely proportional to ''f'' 2, meaning it has higher intensity at lower frequencies, even more so than pink noise. It decreases in intensity by 6 Decibel, dB per Octave (electronics), octave (20 dB per Decade (log scale), decade) and, when heard, has a "damped" or "soft" quality compared to white noise, white and p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electronics Engineering
Electronic engineering is a sub-discipline of electrical engineering that emerged in the early 20th century and is distinguished by the additional use of active components such as semiconductor devices to amplify and control electric current flow. Previously electrical engineering only used passive devices such as mechanical switches, resistors, inductors, and capacitors. It covers fields such as analog electronics, digital electronics, consumer electronics, embedded systems and power electronics. It is also involved in many related fields, for example solid-state physics, radio engineering, telecommunications, control systems, signal processing, systems engineering, computer engineering, instrumentation engineering, electric power control, photonics and robotics. The Institute of Electrical and Electronics Engineers (IEEE) is one of the most important professional bodies for electronics engineers in the US; the equivalent body in the UK is the Institution of Engineering an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Process
In probability theory and statistics, a Gaussian process is a stochastic process (a collection of random variables indexed by time or space), such that every finite collection of those random variables has a multivariate normal distribution. The distribution of a Gaussian process is the joint distribution of all those (infinitely many) random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space. The concept of Gaussian processes is named after Carl Friedrich Gauss because it is based on the notion of the Gaussian distribution (normal distribution). Gaussian processes can be seen as an infinite-dimensional generalization of multivariate normal distributions. Gaussian processes are useful in statistical modelling, benefiting from properties inherited from the normal distribution. For example, if a random process is modelled as a Gaussian process, the distributions of various derived quantities can be obtained explicitly. Such quanti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
White Noise
In signal processing, white noise is a random signal having equal intensity at different frequencies, giving it a constant power spectral density. The term is used with this or similar meanings in many scientific and technical disciplines, including physics, acoustical engineering, telecommunications, and statistical forecasting. White noise refers to a statistical model for signals and signal sources, not to any specific signal. White noise draws its name from white light, although light that appears white generally does not have a flat power spectral density over the visible band. In discrete time, white noise is a discrete signal whose samples are regarded as a sequence of serially uncorrelated random variables with zero mean and finite variance; a single realization of white noise is a random shock. In some contexts, it is also required that the samples be independent and have identical probability distribution (in other words independent and identically distribu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |