|
Werner State
A Werner state is a -dimensional bipartite quantum state density matrix that is invariant under all unitary operators of the form U \otimes U. That is, it is a bipartite quantum state \rho_ that satisfies :\rho_ = (U \otimes U) \rho_ (U^\dagger \otimes U^\dagger) for all unitary operators ''U'' acting on ''d''-dimensional Hilbert space. These states were first developed by Reinhard F. Werner in 1989. General definition Every Werner state W_^ is a mixture of projectors onto the symmetric and antisymmetric subspaces, with the relative weight p \in ,1/math> being the main parameter that defines the state, in addition to the dimension d \geq 2: :W_^ = p \frac P^\text_ + (1-p) \frac P^\text_, where :P^\text_ = \frac(I_+F_), :P^\text_ = \frac(I_-F_), are the projectors and :F_ = \sum_ , i\rangle \langle j, _A \otimes , j\rangle \langle i, _B is the permutation or flip operator that exchanges the two subsystems ''A'' and ''B''. Werner states are separable for ''p'' ≥ and entang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Review A
''Physical Review A'' (also known as PRA) is a monthly peer-reviewed scientific journal published by the American Physical Society covering atomic, molecular, and optical physics and quantum information. the editor was Jan M. Rost ( Max Planck Institute for the Physics of Complex Systems). History In 1893, the '' Physical Review'' was established at Cornell University. It was taken over by the American Physical Society (formed in 1899) in 1913. In 1970, ''Physical Review'' was subdivided into ''Physical Review A'', ''B'', ''C'', and ''D''. At that time, section ''A'' was subtitled ''Physical Review A: General Physics''. In 1990, a process was started to split this journal into two, resulting in the creation of '' Physical Review E'' in 1993. Hence, in 1993, ''Physical Review A'' changed its statement of scope to ''Atomic, Molecular and Optical Physics.'' In January 2007, the section of ''Physical Review E'' that published papers on classical optics was merged into ''Physical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum State
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system represented by the state. Knowledge of the quantum state, and the rules for the system's evolution in time, exhausts all that can be known about a quantum system. Quantum states may be defined differently for different kinds of systems or problems. Two broad categories are * wave functions describing quantum systems using position or momentum variables and * the more abstract vector quantum states. Historical, educational, and application-focused problems typically feature wave functions; modern professional physics uses the abstract vector states. In both categories, quantum states divide into pure versus mixed states, or into coherent states and incoherent states. Categories with special properties include stationary states for tim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariant (mathematics)
In mathematics, an invariant is a property of a mathematical object (or a class of mathematical objects) which remains unchanged after operations or transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used. For example, the area of a triangle is an invariant with respect to isometries of the Euclidean plane. The phrases "invariant under" and "invariant to" a transformation are both used. More generally, an invariant with respect to an equivalence relation is a property that is constant on each equivalence class. Invariants are used in diverse areas of mathematics such as geometry, topology, algebra and discrete mathematics. Some important classes of transformations are defined by an invariant they leave unchanged. For example, conformal maps are defined as transformations of the plane that preserve angles. The discovery of invariants is an import ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unitary Operator
In functional analysis, a unitary operator is a surjective bounded operator on a Hilbert space that preserves the inner product. Non-trivial examples include rotations, reflections, and the Fourier operator. Unitary operators generalize unitary matrices. Unitary operators are usually taken as operating ''on'' a Hilbert space, but the same notion serves to define the concept of isomorphism ''between'' Hilbert spaces. Definition Definition 1. A ''unitary operator'' is a bounded linear operator on a Hilbert space that satisfies , where is the adjoint of , and is the identity operator. The weaker condition defines an ''isometry''. The other weaker condition, , defines a ''coisometry''. Thus a unitary operator is a bounded linear operator that is both an isometry and a coisometry, or, equivalently, a surjective isometry. An equivalent definition is the following: Definition 2. A ''unitary operator'' is a bounded linear operator on a Hilbert space for which the followi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reinhard F
Reinhard is a German, Austrian, Danish, and to a lesser extent Norwegian and Swedish surname (from Germanic ''ragin'', counsel, and ''hart'', strong), and a spelling variant of Reinhardt. Persons with the given name * Reinhard of Blankenburg (after 1107 – 1123), German bishop * Reinhard Böhler (1945–1995), German sidecarcross racer *Reinhard Bonnke (1940–2019), German evangelist * Rainhard Fendrich (born 1955), Austrian singer-songwriter *Reinhard Gehlen (1902–1979), German spymaster * Reinhard Genzel (born 1952), German astrophysicist and Nobel Prize winner *Reinhard Heydrich (1904–1942), German Nazi leader * Reinhard Maack (1892–1969), German explorer * Reinhard Mey (born 1942), German singer *Reinhard Mohn (1921–2009), German media tycoon * Reinhard Odendaal (born 1980), South African award-winning winemaker *Reinhard Scheer (1863–1928), German admiral *Reinhard Selten (1930–2016), German economist *Reinhard Strohm (born 1942), German musicologist * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection (linear Algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself (an endomorphism) such that P\circ P=P. That is, whenever P is applied twice to any vector, it gives the same result as if it were applied once (i.e. P is idempotent). It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object. Definitions A projection on a vector space V is a linear operator P\colon V \to V such that P^2 = P. When V has an inner product and is complete, i.e. when V is a Hilbert space, the concept of orthogonality can be used. A projection P on a Hilbert space V is called an orthogonal projection if it satisfies \langle P \mathbf x, \mathbf y \rangle = \langle \mathbf x, P \mathbf y \rangle for all \mathbf x, \mathbf y \in V. A projecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Separable States
In quantum mechanics, separable states are multipartite quantum states that can be written as a convex combination of product states. Product states are multipartite quantum states that can be written as a tensor product of states in each space. The physical intuition behind these definitions is that product states have no correlation between the different degrees of freedom, while separable states might have correlations, but all such correlations can be explained as due to a classical random variable, as opposed to being due to entanglement. In the special case of pure states the definition simplifies: a pure state is separable if and only if it is a product state. A state is said to be entangled if it is not separable. In general, determining if a state is separable is not straightforward and the problem is classed as NP-hard. Separability of bipartite systems Consider first composite states with two degrees of freedom, referred to as ''bipartite states''. By a postulate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reduction Criterion
In quantum information theory, the reduction criterion is a necessary condition a mixed state must satisfy in order for it to be separable. In other words, the reduction criterion is a ''separability criterion''. It was first proved and independently formulated in 1999. Violation of the reduction criterion is closely related to the distillability of the state in question. Details Let ''H''1 and ''H''2 be Hilbert spaces of finite dimensions ''n'' and ''m'' respectively. ''L''(''Hi'') will denote the space of linear operators acting on ''Hi''. Consider a bipartite quantum system whose state space is the tensor product : H = H_1 \otimes H_2. An (un-normalized) mixed state ''ρ'' is a positive linear operator (density matrix) acting on ''H''. A linear map Φ: ''L''(''H''2) → ''L''(''H''1) is said to be positive if it preserves the cone of positive elements, i.e. ''A'' is positive implied ''Φ''(''A'') is also. From the one-to-one correspondence between positive maps and entangl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
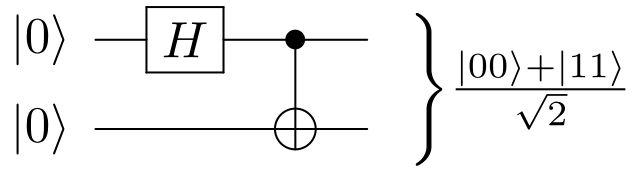
Bell State
In quantum information science, the Bell's states or EPR pairs are specific quantum states of two qubits that represent the simplest examples of quantum entanglement. The Bell's states are a form of entangled and normalized basis vectors. This normalization implies that the overall probability of the particles being in one of the mentioned states is 1: \langle \Phi, \Phi \rangle = 1. Entanglement is a basis-independent result of superposition. Due to this superposition, measurement of the qubit will " collapse" it into one of its basis states with a given probability. Because of the entanglement, measurement of one qubit will "collapse" the other qubit to a state whose measurement will yield one of two possible values, where the value depends on which Bell's state the two qubits are in initially. Bell's states can be generalized to certain quantum states of multi-qubit systems, such as the GHZ state for three or more subsystems. Understanding of Bell's states is useful in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Channel
In quantum information theory, a quantum channel is a communication channel that can transmit quantum information, as well as classical information. An example of quantum information is the general dynamics of a qubit. An example of classical information is a text document transmitted over the Internet. Terminologically, quantum channels are completely positive (CP) trace-preserving maps between spaces of operators. In other words, a quantum channel is just a quantum operation viewed not merely as the reduced dynamics of a system but as a pipeline intended to carry quantum information. (Some authors use the term "quantum operation" to include trace-decreasing maps while reserving "quantum channel" for strictly trace-preserving maps.) Memoryless quantum channel We will assume for the moment that all state spaces of the systems considered, classical or quantum, are finite-dimensional. The memoryless in the section title carries the same meaning as in classical information ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Mathematical Physics
The ''Journal of Mathematical Physics'' is a peer-reviewed journal published monthly by the American Institute of Physics devoted to the publication of papers in mathematical physics. The journal was first published bimonthly beginning in January 1960; it became a monthly publication in 1963. The current editor is Jan Philip Solovej from University of Copenhagen The University of Copenhagen (, KU) is a public university, public research university in Copenhagen, Copenhagen, Denmark. Founded in 1479, the University of Copenhagen is the second-oldest university in Scandinavia, after Uppsala University. .... Its 2018 Impact Factor is 1.355 Abstracting and indexing This journal is indexed by the following services: 2013. References External ...
|