|
Volumetric Flow Rate
In physics and engineering, in particular fluid dynamics, the volumetric flow rate (also known as volume flow rate, or volume velocity) is the volume of fluid which passes per unit time; usually it is represented by the symbol (sometimes \dot V). Its SI unit is cubic metres per second (m3/s). It contrasts with '' mass flow rate'', which is the other main type of fluid flow rate. In most contexts a mention of "rate of fluid flow" is likely to refer to the volumetric rate. In hydrometry, the volumetric flow rate is known as '' discharge''. The volumetric flow rate across a unit area is called '' volumetric flux'', as defined by Darcy's law and represented by the symbol . Conversely, the integration of a volumetric flux over a given area gives the volumetric flow rate. Units The SI unit is cubic metres per second (m3/s). Another unit used is standard cubic centimetres per minute (SCCM). In US customary units and imperial units, volumetric flow rate is often expressed as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sievert
The sievert (symbol: SvPlease note there are two non-SI units that use the same Sv abbreviation: the sverdrup and svedberg.) is a derived unit in the International System of Units (SI) intended to represent the stochastic health risk of ionizing radiation, which is defined as the probability of causing radiation-induced cancer and genetic damage. The sievert is important in dosimetry and radiation protection. It is named after Rolf Maximilian Sievert, a Swedish medical physicist renowned for work on radiation dose measurement and research into the biological effects of radiation. The sievert unit is used for radiation dose quantities such as equivalent dose and effective dose, which represent the risk of external radiation from sources outside the body, and committed dose, which represents the risk of internal irradiation due to inhaled or ingested radioactive substances. According to the International Commission on Radiological Protection (ICRP), one sievert results in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Integral
In mathematics, particularly multivariable calculus, a surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analogue of the line integral. Given a surface, one may integrate over this surface a scalar field (that is, a function of position which returns a scalar as a value), or a vector field (that is, a function which returns a vector as value). If a region R is not flat, then it is called a ''surface'' as shown in the illustration. Surface integrals have applications in physics, particularly in the classical theories of electromagnetism and fluid mechanics. Surface integrals of scalar fields Assume that ''f'' is a scalar, vector, or tensor field defined on a surface ''S''. To find an explicit formula for the surface integral of ''f'' over ''S'', we need to parameterize ''S'' by defining a system of curvilinear coordinates on ''S'', like the latitude and longitude on a sphere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Area
In 3-dimensional geometry and vector calculus, an area vector is a vector combining an area quantity with a direction, thus representing an oriented area in three dimensions. Every bounded surface in three dimensions can be associated with a unique area vector called its vector area. It is equal to the surface integral of the surface normal, and distinct from the usual ( scalar) surface area. Vector area can be seen as the three dimensional generalization of signed area in two dimensions. Definition For a finite planar surface of scalar area and unit normal , the vector area is defined as the unit normal scaled by the area: \mathbf = \hat \mathbfS For an orientable surface composed of a set of flat facet areas, the vector area of the surface is given by \mathbf = \sum_i \hat \mathbf_i S_i where is the unit normal vector to the area . For bounded, oriented curved surfaces that are sufficiently well-behaved, we can still define vector area. First, we split the su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross Section (geometry)
In geometry and science, a cross section is the non-empty intersection (set theory), intersection of a solid body in three-dimensional space with a Plane (geometry), plane, or the analog in higher-dimensional spaces. Cutting an object into slices creates many parallel cross-sections. The boundary of a cross-section in three-dimensional space that is parallel to two of the Cartesian coordinate system, axes, that is, parallel to the plane determined by these axes, is sometimes referred to as a contour line; for example, if a plane cuts through mountains of a raised-relief map parallel to the ground, the result is a contour line in two-dimensional space showing points on the surface of the mountains of equal elevation. In technical drawing a cross-section, being a Planar projection, projection of an object onto a plane that intersects it, is a common tool used to depict the internal arrangement of a 3-dimensional object in two dimensions. It is traditionally crosshatched with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flow Velocity
In continuum mechanics the flow velocity in fluid dynamics, also macroscopic velocity in statistical mechanics, or drift velocity in electromagnetism, is a vector field used to mathematically describe the motion of a continuum. The length of the flow velocity vector is scalar, the ''flow speed''. It is also called velocity field; when evaluated along a line, it is called a velocity profile (as in, e.g., law of the wall). Definition The flow velocity ''u'' of a fluid is a vector field : \mathbf=\mathbf(\mathbf,t), which gives the velocity of an '' element of fluid'' at a position \mathbf\, and time t.\, The flow speed ''q'' is the length of the flow velocity vector :q = \, \mathbf \, and is a scalar field. Uses The flow velocity of a fluid effectively describes everything about the motion of a fluid. Many physical properties of a fluid can be expressed mathematically in terms of the flow velocity. Some common examples follow: Steady flow The flow of a fluid is sai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The definition of length and height (cubed) is interrelated with volume. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid (gas or liquid) that the container could hold, rather than the amount of space the container itself displaces. By metonymy, the term "volume" sometimes is used to refer to the corresponding region (e.g., bounding volume). In ancient times, volume was measured using similar-shaped natural containers. Later on, standardized containers were used. Some simple three-dimensional shapes can have their volume easily calculated using arithmetic formulas. Volumes of more complicated shapes can be calculated with integral calculus if a formula exists for the shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit Of A Function
Although the function is not defined at zero, as becomes closer and closer to zero, becomes arbitrarily close to 1. In other words, the limit of as approaches zero, equals 1. In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input which may or may not be in the domain of the function. Formal definitions, first devised in the early 19th century, are given below. Informally, a function assigns an output to every input . We say that the function has a limit at an input , if gets closer and closer to as moves closer and closer to . More specifically, the output value can be made ''arbitrarily'' close to if the input to is taken ''sufficiently'' close to . On the other hand, if some inputs very close to are taken to outputs that stay a fixed distance apart, then we say the limit ''does not exist''. The notion of a limit has many applications in modern calc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
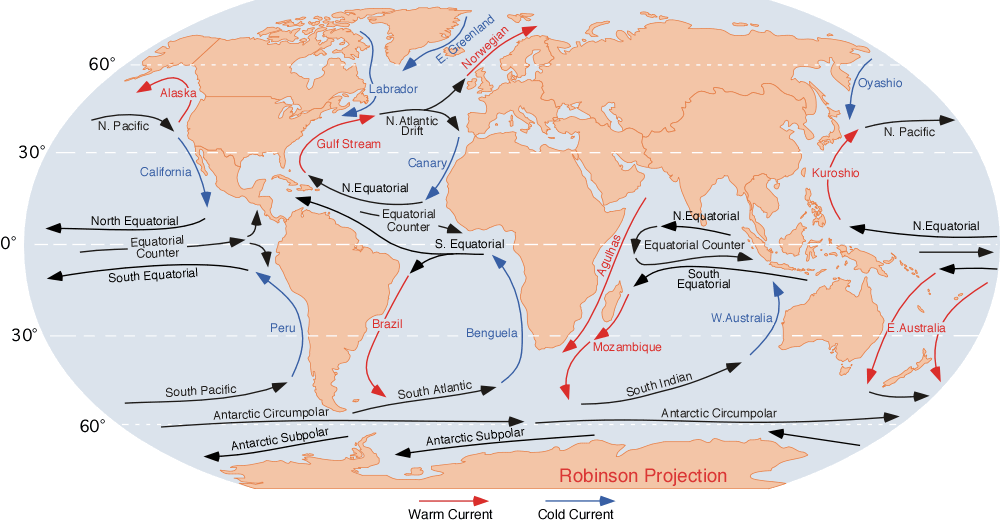
Ocean Current
An ocean current is a continuous, directed movement of seawater generated by a number of forces acting upon the water, including wind, the Coriolis effect, breaking waves, cabbeling, and temperature and salinity differences. Depth contours, shoreline configurations, and interactions with other currents influence a current's direction and strength. Ocean currents move both horizontally, on scales that can span entire oceans, as well as vertically, with vertical currents (upwelling and downwelling) playing an important role in the movement of nutrients and gases, such as carbon dioxide, between the surface and the deep ocean. Ocean currents flow for great distances and together they create the global conveyor belt, which plays a dominant role in determining the climate of many of Earth's regions. More specifically, ocean currents influence the temperature of the regions through which they travel. For example, warm currents traveling along more temperate coasts increase the temper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harald Sverdrup (oceanographer)
Harald Ulrik Sverdrup (15 November 1888 – 21 August 1957) was a Norwegian oceanography, oceanographer and meteorologist. He served as director of the Scripps Institution of Oceanography and the Norwegian Polar Institute. Background He was born at Sogndal in Sogn og Fjordane, Norway. He was the son of Lutheran theologian Edvard Sverdrup (1861–1923) and Maria Vollan (1865–1891). His sister Mimi Sverdrup Lunden (1894–1955) was an educator and author. His brother Leif Sverdrup (1898–1976) was a General with the U.S. Army Corps of Engineers. His brother Einar Sverdrup (1895–1942) was CEO of Store Norske Spitsbergen Kulkompani. Sverdrup was a student at Bergen Cathedral School in 1901 before graduating in 1906 at Kongsgård School in Stavanger. He graduated cand. real. in 1914 from University of Oslo. He studied under Vilhelm Bjerknes and earned his Dr. Philos. at the University of Leipzig in 1917. Career He was the scientific director of the North Pole, North ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hectometer
The hectometre, ( SI symbol: hm), spelt hectometer in American and Philippine English, is a unit of length in the International System of Units (SI), equal to one hundred metres and to one tenth of a kilometre. The word comes from a combination of "metre" and the SI prefix " hecto-", meaning "hundred". It is not commonly used in English. A football field (either soccer or American) is approximately 1 hectometre in length. The hectare (ha), a common metric unit for land area, is equal to one square hectometre (hm2). The hectometer has sometimes been used for expressing the distance to a target in warfare. See also *Orders of magnitude (length) The following are examples of order of magnitude, orders of magnitude for different lengths. Overview Detailed list To help compare different orders of magnitude, the following list describes various lengths between 1.6 \times 10^ me ... * Conversion of units References External links * {{DEFAULTSORT:Hectometre + ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rosenstiel School Of Marine, Atmospheric, And Earth Science
The Rosenstiel School of Marine, Atmospheric, and Earth Science is the University of Miami's academic and research institution for the study of oceanography, atmospheric sciences, atmospheric, and earth sciences. The Rosenstiel School is located east from the University of Miami's main Coral Gables, Florida, Coral Gables campus on Virginia Key in Miami, Florida, United States. Founded in 1943, the University of Miami's Rosenstiel School is the only subtropical applied and basic marine, atmospheric, and earth research institute in the continental United States. The school is also home to SUSTAIN, the world's largest hurricane simulation tank. Up until 2008, Rosenstiel School was solely a graduate school within the University of Miami, though it jointly administrated an undergraduate education, undergraduate program with the University of Miami's College of Arts and Sciences. In 2008, Rosenstiel School launched an undergraduate program, granting both Bachelor of Science in Mari ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |