|
Variational Analysis
In mathematics, variational analysis is the combination and extension of methods from convex optimization and the classical calculus of variations to a more general theory. This includes the more general problems of optimization theory, including topics in set-valued analysis, e.g. generalized derivatives. In the Mathematics Subject Classification scheme (MSC2010), the field of "Set-valued and variational analysis" is coded by "49J53". History While this area of mathematics has a long history, the first use of the term "Variational analysis" in this sense was in an eponymous book by R. Tyrrell Rockafellar and Roger J-B Wets. Existence of minima A classical result is that a lower semicontinuous function on a compact set attains its minimum. Results from variational analysis such as Ekeland's variational principle allow us to extend this result of lower semicontinuous functions on non-compact sets provided that the function has a lower bound and at the cost of adding a sm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermat's Theorem (stationary Points)
In mathematics, the interior extremum theorem, also known as Fermat's theorem, is a theorem which states that at the local extrema of a differentiable function, its derivative is always zero. It belongs to the mathematical field of real analysis and is named after French mathematician Pierre de Fermat. By using the interior extremum theorem, the potential extrema of a function f, with derivative f', can found by solving an equation involving f'. The interior extremum theorem gives only a necessary condition for extreme function values, as some stationary points are inflection points (not a maximum or minimum). The function's second derivative, if it exists, can sometimes be used to determine whether a stationary point is a maximum or minimum. History Pierre de Fermat proposed in a collection of treatises titled ''Maxima et minima'' a method to find maximum or minimum, similar to the modern interior extremum theorem, albeit with the use of infinitesimals rather than derivatives ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locally Lipschitz
In mathematical analysis, Lipschitz continuity, named after German mathematician Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: there exists a real number such that, for every pair of points on the graph of this function, the absolute value of the slope of the line connecting them is not greater than this real number; the smallest such bound is called the ''Lipschitz constant'' of the function (and is related to the '' modulus of uniform continuity''). For instance, every function that is defined on an interval and has a bounded first derivative is Lipschitz continuous. In the theory of differential equations, Lipschitz continuity is the central condition of the Picard–Lindelöf theorem which guarantees the existence and uniqueness of the solution to an initial value problem. A special type of Lipschitz continuity, called contraction, is used in the Banach fixed-point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clarke Generalized Derivative
In mathematics, the Clarke generalized derivatives are types generalized of derivatives that allow for the differentiation of nonsmooth functions. The Clarke derivatives were introduced by Francis Clarke in 1975. Definitions For a locally Lipschitz continuous function f: \mathbb^ \rightarrow \mathbb, the ''Clarke generalized directional derivative'' of f at x \in \mathbb^n in the direction v \in \mathbb^n is defined as f^ (x, v)= \limsup_ \frac, where \limsup denotes the limit supremum. Then, using the above definition of f^, the ''Clarke generalized gradient'' of f at x (also called the ''Clarke subdifferential'') is given as \partial^\! f(x):=\, where \langle \cdot, \cdot\rangle represents an inner product of vectors in \mathbb. Note that the Clarke generalized gradient is set-valued—that is, at each x \in \mathbb^n, the function value \partial^\! f(x) is a set. More generally, given a Banach space X and a subset Y \subset X, the Clarke generalized directional deriv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subderivative
In mathematics, the subderivative (or subgradient) generalizes the derivative to convex functions which are not necessarily differentiable. The set of subderivatives at a point is called the subdifferential at that point. Subderivatives arise in convex analysis, the study of convex functions, often in connection to convex optimization. Let f:I \to \mathbb be a real-valued convex function defined on an open interval of the real line. Such a function need not be differentiable at all points: For example, the absolute value function f(x)=, x, is non-differentiable when x=0. However, as seen in the graph on the right (where f(x) in blue has non-differentiable kinks similar to the absolute value function), for any x_0 in the domain of the function one can draw a line which goes through the point (x_0,f(x_0)) and which is everywhere either touching or below the graph of ''f''. The slope of such a line is called a ''subderivative''. Definition Rigorously, a ''subderivative'' of a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Function
In mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of a function, graph of the function lies above or on the graph between the two points. Equivalently, a function is convex if its epigraph (mathematics), ''epigraph'' (the set of points on or above the graph of the function) is a convex set. In simple terms, a convex function graph is shaped like a cup \cup (or a straight line like a linear function), while a concave function's graph is shaped like a cap \cap. A twice-differentiable function, differentiable function of a single variable is convex if and only if its second derivative is nonnegative on its entire domain of a function, domain. Well-known examples of convex functions of a single variable include a linear function f(x) = cx (where c is a real number), a quadratic function cx^2 (c as a nonnegative real number) and an exponential function ce^x (c as a nonnegative real number). Convex functions pl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrange Multiplier
In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function (mathematics), function subject to constraint (mathematics), equation constraints (i.e., subject to the condition that one or more equations have to be satisfied exactly by the chosen values of the variable (mathematics), variables). It is named after the mathematician Joseph-Louis Lagrange. Summary and rationale The basic idea is to convert a constrained problem into a form such that the derivative test of an unconstrained problem can still be applied. The relationship between the gradient of the function and gradients of the constraints rather naturally leads to a reformulation of the original problem, known as the Lagrangian function or Lagrangian. In the general case, the Lagrangian is defined as \mathcal(x, \lambda) \equiv f(x) + \langle \lambda, g(x)\rangle for functions f, g; the notation \langle \cdot, \cdot \rangle denotes an inner prod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smooth Function
In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives (''differentiability class)'' it has over its domain. A function of class C^k is a function of smoothness at least ; that is, a function of class C^k is a function that has a th derivative that is continuous in its domain. A function of class C^\infty or C^\infty-function (pronounced C-infinity function) is an infinitely differentiable function, that is, a function that has derivatives of all orders (this implies that all these derivatives are continuous). Generally, the term smooth function refers to a C^-function. However, it may also mean "sufficiently differentiable" for the problem under consideration. Differentiability classes Differentiability class is a classification of functions according to the properties of their derivatives. It is a measure of the highest order of derivative that exists and is continuous for a function. Consider an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation. There are multiple different notations for differentiation. '' Leibniz notation'', named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas ''prime notation'' is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ekeland's Variational Principle
In mathematical analysis, Ekeland's variational principle, discovered by Ivar Ekeland, is a theorem that asserts that there exist nearly optimal solutions to some optimization problems. Ekeland's principle can be used when the lower level set of a minimization problems is not compact, so that the Bolzano–Weierstrass theorem cannot be applied. The principle relies on the completeness of the metric space. The principle has been shown to be equivalent to completeness of metric spaces. In proof theory, it is equivalent to ΠCA0 over RCA0, i.e. relatively strong. It also leads to a quick proof of the Caristi fixed point theorem. History Ekeland was associated with the Paris Dauphine University when he proposed this theorem. Ekeland's variational principle Preliminary definitions A function f : X \to \R \cup \ valued in the extended real numbers \R \cup \ = \infty, +\infty/math> is said to be if \inf_ f(X) = \inf_ f(x) > -\infty and it is called if it has a non-empty , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
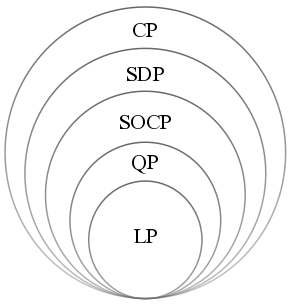
Convex Optimization
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization problems admit polynomial-time algorithms, whereas mathematical optimization is in general NP-hard. Definition Abstract form A convex optimization problem is defined by two ingredients: * The ''objective function'', which is a real-valued convex function of ''n'' variables, f :\mathcal D \subseteq \mathbb^n \to \mathbb; * The ''feasible set'', which is a convex subset C\subseteq \mathbb^n. The goal of the problem is to find some \mathbf \in C attaining :\inf \. In general, there are three options regarding the existence of a solution: * If such a point ''x''* exists, it is referred to as an ''optimal point'' or ''solution''; the set of all optimal points is called the ''optimal set''; and the problem is called ''solvable''. * If f is unbou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compact Set
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space. The idea is that a compact space has no "punctures" or "missing endpoints", i.e., it includes all ''limiting values'' of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval ,1would be compact. Similarly, the space of rational numbers \mathbb is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers \mathbb is not compact either, because it excludes the two limiting values +\infty and -\infty. However, the ''extended'' real number line ''would'' be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topological spaces. One su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |