|
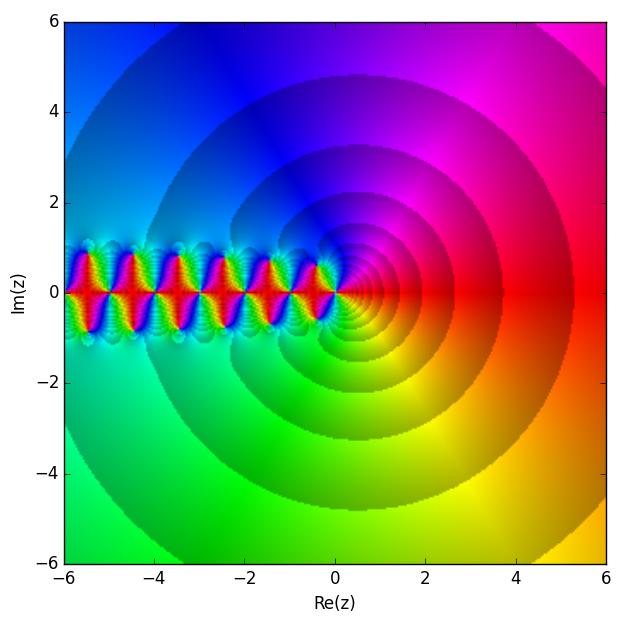
Trigamma Function
In mathematics, the trigamma function, denoted or , is the second of the polygamma functions, and is defined by : \psi_1(z) = \frac \ln\Gamma(z). It follows from this definition that : \psi_1(z) = \frac \psi(z) where is the digamma function. It may also be defined as the sum of the series : \psi_1(z) = \sum_^\frac, making it a special case of the Hurwitz zeta function : \psi_1(z) = \zeta(2,z). Note that the last two formulas are valid when is not a natural number. Calculation A double integral representation, as an alternative to the ones given above, may be derived from the series representation: : \psi_1(z) = \int_0^1\!\!\int_0^x\frac\,dy\,dx using the formula for the sum of a geometric series. Integration over yields: : \psi_1(z) = -\int_0^1\frac\,dx An asymptotic expansion as a Laurent series can be obtained via the derivative of the asymptotic expansion of the digamma function: :\begin \psi_1(z) &\sim \left(\ln z - \sum_^\infty \frac\right) \\ &= \fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digamma Function
In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function: :\psi(z) = \frac\ln\Gamma(z) = \frac. It is the first of the polygamma functions. This function is Monotonic function, strictly increasing and Concave function, strictly concave on (0,\infty), and it Asymptotic analysis, asymptotically behaves as :\psi(z) \sim \ln - \frac, for complex numbers with large modulus (, z, \rightarrow\infty) in the Circular sector, sector , \arg z, 0. The digamma function is often denoted as \psi_0(x), \psi^(x) or (the uppercase form of the archaic Greek consonant digamma meaning Gamma, double-gamma). Gamma. Relation to harmonic numbers The gamma function obeys the equation :\Gamma(z+1)=z\Gamma(z). \, Taking the logarithm on both sides and using the functional equation property of the log-gamma function gives: :\log \Gamma(z+1)=\log(z)+\log \Gamma(z), Differentiating both sides with respect to gives: :\psi(z+1)=\psi(z)+\frac Since the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygamma Function
In mathematics, the polygamma function of order is a meromorphic function on the complex numbers \mathbb defined as the th derivative of the logarithm of the gamma function: :\psi^(z) := \frac \psi(z) = \frac \ln\Gamma(z). Thus :\psi^(z) = \psi(z) = \frac holds where is the digamma function and is the gamma function. They are holomorphic on \mathbb \backslash\mathbb_. At all the nonpositive integers these polygamma functions have a pole of order . The function is sometimes called the trigamma function. Integral representation When and , the polygamma function equals :\begin \psi^(z) &= (-1)^\int_0^\infty \frac\,\mathrmt \\ &= -\int_0^1 \frac(\ln t)^m\,\mathrmt\\ &= (-1)^m!\zeta(m+1,z) \end where \zeta(s,q) is the Hurwitz zeta function. This expresses the polygamma function as the Laplace transform of . It follows from Bernstein's theorem on monotone functions that, for and real and non-negative, is a completely monotone function. Setting in the above ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by Γ, capital Greek alphabet, Greek letter gamma) is the most common extension of the factorial function to complex numbers. Derived by Daniel Bernoulli, the gamma function \Gamma(z) is defined for all complex numbers z except non-positive integers, and for every positive integer z=n, \Gamma(n) = (n-1)!\,.The gamma function can be defined via a convergent improper integral for complex numbers with positive real part: \Gamma(z) = \int_0^\infty t^ e^\textt, \ \qquad \Re(z) > 0\,.The gamma function then is defined in the complex plane as the analytic continuation of this integral function: it is a meromorphic function which is holomorphic function, holomorphic except at zero and the negative integers, where it has simple Zeros and poles, poles. The gamma function has no zeros, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clausen Function
In mathematics, the Clausen function, introduced by , is a transcendental, special function of a single variable. It can variously be expressed in the form of a definite integral, a trigonometric series, and various other forms. It is intimately connected with the polylogarithm, inverse tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function. The Clausen function of order 2 – often referred to as ''the'' Clausen function, despite being but one of a class of many – is given by the integral: :\operatorname_2(\varphi)=-\int_0^\varphi \log\left, 2\sin\frac \\, dx: In the range 0 :\operatorname_2\left(-\frac+2m\pi \right) =-1.01494160 \ldots The following properties are immediate consequences of the series definition: :\operatorname_2(\theta+2m\pi) = \operatorname_2(\theta) :\operatorname_2(-\theta) = -\operatorname_2(\theta) See . General definition More generally, one defines the two generalized Clausen fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catalan's Constant
In mathematics, Catalan's constant , is the alternating sum of the reciprocals of the odd square numbers, being defined by: : G = \beta(2) = \sum_^ \frac = \frac - \frac + \frac - \frac + \frac - \cdots, where is the Dirichlet beta function. Its numerical value is approximately : Catalan's constant was named after Eugène Charles Catalan, who found quickly-converging series for its calculation and published a memoir on it in 1865. Uses In low-dimensional topology, Catalan's constant is 1/4 of the volume of an ideal hyperbolic octahedron, and therefore 1/4 of the hyperbolic volume of the complement of the Whitehead link. It is 1/8 of the volume of the complement of the Borromean rings. In combinatorics and statistical mechanics, it arises in connection with counting domino tilings, spanning trees, and Hamiltonian cycles of grid graphs. In number theory, Catalan's constant appears in a conjectured formula for the asymptotic number of primes of the form n^2+1 accordin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reflection Formula
In mathematics, a reflection formula or reflection relation for a function is a relationship between and . It is a special case of a functional equation. It is common in mathematical literature to use the term "functional equation" for what are specifically reflection formulae. Reflection formulae are useful for numerical computation of special functions. In effect, an approximation that has greater accuracy or only converges on one side of a reflection point (typically in the positive half of the complex plane) can be employed for all arguments. Known formulae The even and odd functions satisfy by definition simple reflection relations around . For all even functions, f(-x) = f(x), and for all odd functions, f(-x) = -f(x). A famous relationship is Euler's reflection formula \Gamma(z)\Gamma(1-z) = \frac, \qquad z \not\in \mathbb Z for the gamma function \Gamma(z), due to Leonhard Euler. There is also a reflection formula for the general -th order polygamma function , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recurrence Relation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter k that is independent of n; this number k is called the ''order'' of the relation. If the values of the first k numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation. In ''linear recurrences'', the th term is equated to a linear function of the k previous terms. A famous example is the recurrence for the Fibonacci numbers, F_n=F_+F_ where the order k is two and the linear function merely adds the two previous terms. This example is a linear recurrence with constant coefficients, because the coefficients of the linear function (1 and 1) are constants that do not depend on n. For these recurrences, one can express the general term of the sequence as a closed-form expression o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli Number
In mathematics, the Bernoulli numbers are a sequence of rational numbers which occur frequently in analysis. The Bernoulli numbers appear in (and can be defined by) the Taylor series expansions of the tangent and hyperbolic tangent functions, in Faulhaber's formula for the sum of ''m''-th powers of the first ''n'' positive integers, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function. The values of the first 20 Bernoulli numbers are given in the adjacent table. Two conventions are used in the literature, denoted here by B^_n and B^_n; they differ only for , where B^_1=-1/2 and B^_1=+1/2. For every odd , . For every even , is negative if is divisible by 4 and positive otherwise. The Bernoulli numbers are special values of the Bernoulli polynomials B_n(x), with B^_n=B_n(0) and B^+_n=B_n(1). The Bernoulli numbers were discovered around the same time by the Swiss mathematician Jacob Bernoulli, after whom they are named, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laurent Series
In mathematics, the Laurent series of a complex function f(z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass had previously described it in a paper written in 1841 but not published until 1894. Definition The Laurent series for a complex function f(z) about an arbitrary point c is given by f(z) = \sum_^\infty a_n(z-c)^n, where the coefficients a_n are defined by a contour integral that generalizes Cauchy's integral formula: a_n =\frac\oint_\gamma \frac \, dz. The path of integration \gamma is counterclockwise around a Jordan curve enclosing c and lying in an annulus A in which f(z) is holomorphic ( analytic). The expansion for f(z) will then be valid anywhere inside the annulus. The annulus is shown in red in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Series
In mathematics, a geometric series is a series (mathematics), series summing the terms of an infinite geometric sequence, in which the ratio of consecutive terms is constant. For example, 1/2 + 1/4 + 1/8 + 1/16 + ⋯, the series \tfrac12 + \tfrac14 + \tfrac18 + \cdots is a geometric series with common ratio , which converges to the sum of . Each term in a geometric series is the geometric mean of the term before it and the term after it, in the same way that each term of an arithmetic series is the arithmetic mean of its neighbors. While Ancient Greek philosophy, Greek philosopher Zeno's paradoxes about time and motion (5th century BCE) have been interpreted as involving geometric series, such series were formally studied and applied a century or two later by Greek mathematics, Greek mathematicians, for example used by Archimedes to Quadrature of the Parabola, calculate the area inside a parabola (3rd century BCE). Today, geometric series are used in mathematical finance, calculati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |