|
Toniann Pitassi
Toniann Pitassi is a Canadian and American mathematician and computer scientist specializing in computational complexity theory. She is currently Jeffrey L. and Brenda Bleustein Professor of Engineering at Columbia University and was Bell Research Chair at the University of Toronto. Academic career A native of Pittsburgh, Pitassi earned bachelor's and master's degrees at Pennsylvania State University before moving to the University of Toronto for her doctoral studies; she earned her Ph.D. in 1992 from Toronto under the supervision of Stephen Cook. After postdoctoral studies at the University of California, San Diego and faculty positions at the University of Pittsburgh and University of Arizona, she returned to Toronto in 2001, and was a professor in the University of Toronto Department of Computer Science and University of Toronto Department of Mathematics until 2021, when she joined the faculty of Columbia University. She was an invited speaker at International Congress of Ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Research Institute Of Oberwolfach
The Oberwolfach Research Institute for Mathematics (german: Mathematisches Forschungsinstitut Oberwolfach) is a center for mathematical research in Oberwolfach, Germany. It was founded by mathematician Wilhelm Süss in 1944. It organizes weekly workshops on diverse topics where mathematicians and scientists from all over the world come to do collaborative research. The Institute is a member of the Leibniz Association, funded mainly by the German Federal Ministry of Education and Research and by the state of Baden-Württemberg. It also receives substantial funding from the ''Friends of Oberwolfach'' foundation, from the ''Oberwolfach Foundation'' and from numerous donors. History The Oberwolfach Research Institute for Mathematics (MFO) was founded as the ''Reich Institute of Mathematics'' (German: ''Reichsinstitut für Mathematik'') on 1 September 1944. It was one of several research institutes founded by the Nazis in order to further the German war effort, which at that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symposium On Theory Of Computing
The Annual ACM Symposium on Theory of Computing (STOC) is an academic conference in the field of theoretical computer science. STOC has been organized annually since 1969, typically in May or June; the conference is sponsored by the Association for Computing Machinery special interest group SIGACT. Acceptance rate of STOC, averaged from 1970 to 2012, is 31%, with the rate of 29% in 2012. As writes, STOC and its annual IEEE counterpart FOCS (the Symposium on Foundations of Computer Science) are considered the two top conferences in theoretical computer science, considered broadly: they “are forums for some of the best work throughout theory of computing that promote breadth among theory of computing researchers and help to keep the community together.” includes regular attendance at STOC and FOCS as one of several defining characteristics of theoretical computer scientists. Awards The Gödel Prize for outstanding papers in theoretical computer science is presented alternately ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
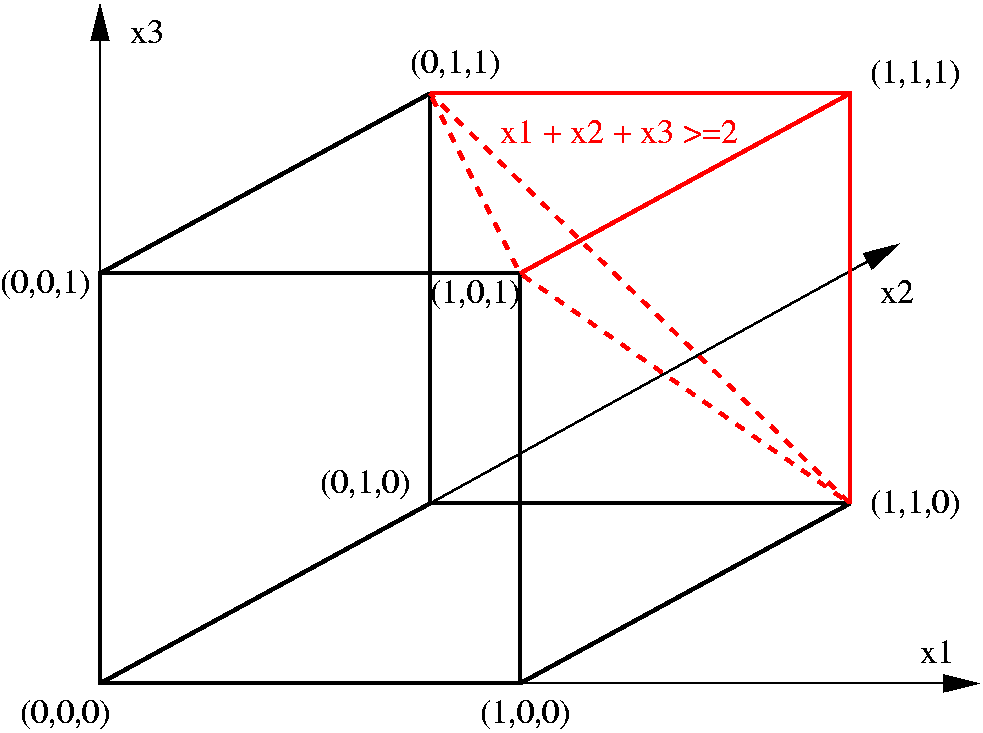
3-satisfiability
In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called ''satisfiable''. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is ''unsatisfiable''. For example, the formula "''a'' AND NOT ''b''" is satisfiable because one can find the values ''a'' = TRUE and ''b'' = FALSE, which make (''a'' AND NOT ''b'') = TRUE. In contrast, "''a'' AND NOT ''a''" is unsatisfiable. SAT is the first problem that was proved to be NP-complete; ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resolution (logic)
In mathematical logic and automated theorem proving, resolution is a rule of inference leading to a refutation complete theorem-proving technique for sentences in propositional logic and first-order logic. For propositional logic, systematically applying the resolution rule acts as a decision procedure for formula unsatisfiability, solving the (complement of the) Boolean satisfiability problem. For first-order logic, resolution can be used as the basis for a semi-algorithm for the unsatisfiability problem of first-order logic, providing a more practical method than one following from Gödel's completeness theorem. The resolution rule can be traced back to Davis and Putnam (1960); however, their algorithm required trying all ground instances of the given formula. This source of combinatorial explosion was eliminated in 1965 by John Alan Robinson's syntactical unification algorithm, which allowed one to instantiate the formula during the proof "on demand" just as far as need ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum Clique Problem
In computer science, the clique problem is the computational problem of finding cliques (subsets of vertices, all adjacent to each other, also called complete subgraphs) in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique (a clique with the largest possible number of vertices), finding a maximum weight clique in a weighted graph, listing all maximal cliques (cliques that cannot be enlarged), and solving the decision problem of testing whether a graph contains a clique larger than a given size. The clique problem arises in the following real-world setting. Consider a social network, where the graph's vertices represent people, and the graph's edges represent mutual acquaintance. Then a clique represents a subset of people who all know each other, and algorithms for finding cliques can be used to discover these groups of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cutting-plane Method
In mathematical optimization, the cutting-plane method is any of a variety of optimization methods that iteratively refine a feasible set or objective function by means of linear inequalities, termed ''cuts''. Such procedures are commonly used to find integer solutions to mixed integer linear programming (MILP) problems, as well as to solve general, not necessarily differentiable convex optimization problems. The use of cutting planes to solve MILP was introduced by Ralph E. Gomory. Cutting plane methods for MILP work by solving a non-integer linear program, the linear relaxation of the given integer program. The theory of Linear Programming dictates that under mild assumptions (if the linear program has an optimal solution, and if the feasible region does not contain a line), one can always find an extreme point or a corner point that is optimal. The obtained optimum is tested for being an integer solution. If it is not, there is guaranteed to exist a linear inequality th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pigeonhole Principle
In mathematics, the pigeonhole principle states that if items are put into containers, with , then at least one container must contain more than one item. For example, if one has three gloves (and none is ambidextrous/reversible), then there must be at least two right-handed gloves, or at least two left-handed gloves, because there are three objects, but only two categories of handedness to put them into. This seemingly obvious statement, a type of counting argument, can be used to demonstrate possibly unexpected results. For example, given that the population of London is greater than the maximum number of hairs that can be present on a human's head, then the pigeonhole principle requires that there must be at least two people in London who have the same number of hairs on their heads. Although the pigeonhole principle appears as early as 1624 in a book attributed to Jean Leurechon, it is commonly called Dirichlet's box principle or Dirichlet's drawer principle after an 1834 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frege System
In proof complexity, a Frege system is a propositional proof system whose proofs are sequences of formulas derived using a finite set of sound and implicationally complete inference rules. Frege systems (more often known as Hilbert systems in general proof theory) are named after Gottlob Frege. Formal definition Let ''K'' be a finite functionally complete set of Boolean connectives, and consider propositional formulas built from variables ''p''0, ''p''1, ''p''2, ... using ''K''-connectives. A Frege rule is an inference rule of the form :r=\fracB, where ''B''1, ..., ''Bn'', ''B'' are formulas. If ''R'' is a finite set of Frege rules, then ''F'' = (''K'',''R'') defines a derivation system in the following way. If ''X'' is a set of formulas, and ''A'' is a formula, then an ''F''-derivation of ''A'' from axioms ''X'' is a sequence of formulas ''A''1, ..., ''Am'' such that ''Am'' = ''A'', and every ''Ak'' is a member of ''X'', or it is derived from some of the formulas ''Ai'', ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Complexity
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is generally express ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proposition
In logic and linguistics, a proposition is the meaning of a declarative sentence. In philosophy, "meaning" is understood to be a non-linguistic entity which is shared by all sentences with the same meaning. Equivalently, a proposition is the non-linguistic bearer of truth or falsity which makes any sentence that expresses it either true or false. While the term "proposition" may sometimes be used in everyday language to refer to a linguistic statement which can be either true or false, the technical philosophical term, which differs from the mathematical usage, refers exclusively to the non-linguistic meaning behind the statement. The term is often used very broadly and can also refer to various related concepts, both in the history of philosophy and in contemporary analytic philosophy. It can generally be used to refer to some or all of the following: The primary bearers of truth values (such as "true" and "false"); the objects of belief and other propositional attitudes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Proof
A mathematical proof is an Inference, inferential Argument-deduction-proof distinctions, argument for a Proposition, mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning which establish logical certainty, to be distinguished from empirical evidence, empirical arguments or non-exhaustive inductive reasoning which establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in ''all'' possible cases. A proposition that has not been proved but is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for furthe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Upper And Lower Bounds
In mathematics, particularly in order theory, an upper bound or majorant of a subset of some preordered set is an element of that is greater than or equal to every element of . Dually, a lower bound or minorant of is defined to be an element of that is less than or equal to every element of . A set with an upper (respectively, lower) bound is said to be bounded from above or majorized (respectively bounded from below or minorized) by that bound. The terms bounded above (bounded below) are also used in the mathematical literature for sets that have upper (respectively lower) bounds. Examples For example, is a lower bound for the set (as a subset of the integers or of the real numbers, etc.), and so is . On the other hand, is not a lower bound for since it is not smaller than every element in . The set has as both an upper bound and a lower bound; all other numbers are either an upper bound or a lower bound for that . Every subset of the natural numbers has a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |