|
Three-body Problem
In physics, specifically classical mechanics, the three-body problem is to take the initial positions and velocities (or momenta) of three point masses orbiting each other in space and then calculate their subsequent trajectories using Newton's laws of motion and Newton's law of universal gravitation. Unlike the two-body problem, the three-body problem has no general closed-form solution, meaning there is no equation that always solves it. When three bodies orbit each other, the resulting dynamical system is chaotic for most initial conditions. Because there are no solvable equations for most three-body systems, the only way to predict the motions of the bodies is to estimate them using numerical methods. The three-body problem is a special case of the -body problem. Historically, the first specific three-body problem to receive extended study was the one involving the Earth, the Moon, and the Sun. In an extended modern sense, a three-body problem is any problem in classic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-body Problem Animation With COM
''Three-Body'' () is a Chinese language, Chinese science fiction television series Adapted screenplay, adapted from the novel ''The Three-Body Problem (novel), The Three-Body Problem'' by Liu Cixin, which was first published in serialized form in 2006. The series premiered on January 15, 2023. Premise In 2007, Wang Miao, one of China's leading nanomaterials experts, is enlisted by Shi Qiang, a detective who specializes in counterterrorism, in cases of strange apparent suicides in the scientific community. During their investigation they encounter a mysterious organization called "The Frontiers of Science" and proceed to learn the truth behind how an Extraterrestrial intelligence, extraterrestrial world depicted in a popular video game connects with the fate of humanity on Earth. Cast * Zhang Luyi as Wang Miao * Yu Hewei as detective Shi Qiang * Chen Jin (actress), Chen Jin and Wang Ziwen as Ye Wenjie * Lin Yongjian as General Chang Weisi * Li Xiaoran as Shen Yufei * Eric Wang a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Horseshoe Orbit
In celestial mechanics, a horseshoe orbit is a type of co-orbital motion of a small orbiting body relative to a larger orbiting body. The osculating (instantaneous) orbital period of the smaller body remains very near that of the larger body, and if its orbit is a little more eccentric than that of the larger body, during every period it appears to trace an ellipse around a point on the larger object's orbit. However, the loop is not closed but drifts forward or backward so that the point it circles will appear to move smoothly along the larger body's orbit over a long period of time. When the object approaches the larger body closely at either end of its trajectory, its apparent direction changes. Over an entire cycle the center traces the outline of a horseshoe, with the larger body between the 'horns'. Asteroids in horseshoe orbits with respect to Earth include 54509 YORP, , , and possibly . A broader definition includes 3753 Cruithne, which can be said to be in a compound ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrangian Points
In celestial mechanics, the Lagrange points (; also Lagrangian points or libration points) are points of equilibrium for small-mass objects under the gravitational influence of two massive orbiting bodies. Mathematically, this involves the solution of the restricted three-body problem. Normally, the two massive bodies exert an unbalanced gravitational force at a point, altering the orbit of whatever is at that point. At the Lagrange points, the gravitational forces of the two large bodies and the centrifugal force balance each other. This can make Lagrange points an excellent location for satellites, as orbit corrections, and hence fuel requirements, needed to maintain the desired orbit are kept at a minimum. For any combination of two orbital bodies, there are five Lagrange points, L1 to L5, all in the orbital plane of the two large bodies. There are five Lagrange points for the Sun–Earth system, and five ''different'' Lagrange points for the Earth–Moon system. L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotating Reference Frame
A rotating frame of reference is a special case of a non-inertial reference frame that is rotation, rotating relative to an inertial reference frame. An everyday example of a rotating reference frame is the surface of the Earth. (This article considers only frames rotating about a fixed axis. For more general rotations, see Euler angles#Vehicles and moving frames, Euler angles.) Fictitious forces All non-inertial reference frames exhibit fictitious forces; rotating reference frames are characterized by three: * the centrifugal force (fictitious), centrifugal force, * the Coriolis force, and, for non-uniformly rotating reference frames, * the Euler force. Scientists in a rotating box can measure the rotation speed and axis of rotation by measuring these fictitious forces. For example, Léon Foucault was able to show the Coriolis force that results from Earth's rotation using the Foucault pendulum. If Earth were to rotate many times faster, these fictitious forces could be fel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
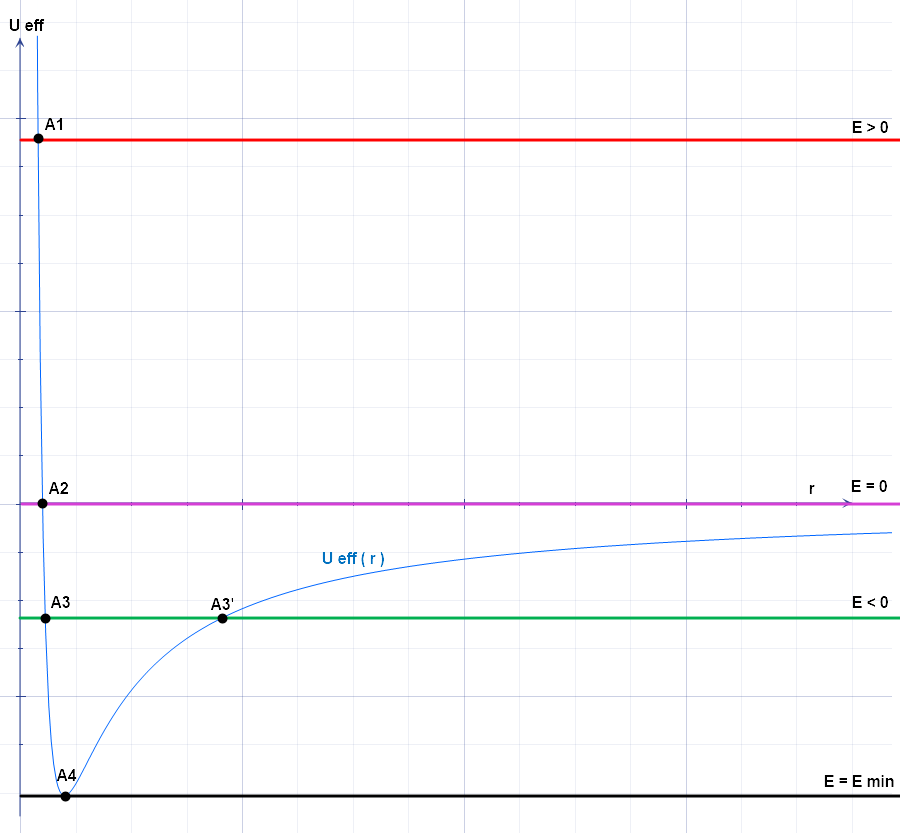
Effective Potential
The effective potential (also known as effective potential energy) combines multiple, perhaps opposing, effects into a single potential. In its basic form, it is the sum of the "opposing" centrifugal potential energy with the potential energy of a dynamical system. It may be used to determine the orbits of planets (both Newtonian and relativistic) and to perform semi-classical atomic calculations, and often allows problems to be reduced to fewer dimensions. Definition The basic form of potential U_\text is defined as U_\text(\mathbf) = \frac + U(\mathbf), where : ''L'' is the angular momentum, : ''r'' is the distance between the two masses, : ''μ'' is the reduced mass of the two bodies (approximately equal to the mass of the orbiting body if one mass is much larger than the other), : ''U''(''r'') is the general form of the potential. The effective force, then, is the negative gradient of the effective potential: \begin \mathbf_\text &= -\nabla U_\text(\mathbf) \\ &= \fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Center Of Mass
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the barycenter or balance point) is the unique point at any given time where the weight function, weighted relative position (vector), position of the distributed mass sums to zero. For a rigid body containing its center of mass, this is the point to which a force may be applied to cause a linear acceleration without an angular acceleration. Calculations in mechanics are often simplified when formulated with respect to the center of mass. It is a hypothetical point where the entire mass of an object may be assumed to be concentrated to visualise its motion. In other words, the center of mass is the particle equivalent of a given object for application of Newton's laws of motion. In the case of a single rigid body, the center of mass is fixed in relation to the body, and if the body has uniform density, it will be located at the centroid. The center of mass may be located outside the Phys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Restricted Three-Body Problem - Energy Potential Analysis
Restricted may refer to: * R rating (other), list of subjects where "R" stands for "Restricted" *18 rating, media rating designation sometimes called "Restricted" * Restricted (country club), historical use of the term in country clubs in the United States * Restricted airspace, airspace for which air traffic is restricted or prohibited for safety or security concerns * Restricted area, several uses *Restricted free agent, a type of free agent in various professional sports * Restricted list, a roster status in Major League Baseball *Restricted stock Restricted stock, also known as restricted securities, is stock of a company that is not fully transferable (from the stock-issuing company to the person receiving the stock award) until certain conditions (restrictions) have been met. Upon satisfa ..., stock of a company that is not fully transferable See also * * Restrict, keyword in the C programming language * Restriction (other) {{Disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian Mechanics
In physics, Hamiltonian mechanics is a reformulation of Lagrangian mechanics that emerged in 1833. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities \dot q^i used in Lagrangian mechanics with (generalized) ''momenta''. Both theories provide interpretations of classical mechanics and describe the same physical phenomena. Hamiltonian mechanics has a close relationship with geometry (notably, symplectic geometry and Poisson structures) and serves as a Hamilton–Jacobi equation, link between classical and quantum mechanics. Overview Phase space coordinates (''p'', ''q'') and Hamiltonian ''H'' Let (M, \mathcal L) be a Lagrangian mechanics, mechanical system with configuration space (physics), configuration space M and smooth Lagrangian_mechanics#Lagrangian, Lagrangian \mathcal L. Select a standard coordinate system (\boldsymbol,\boldsymbol) on M. The quantities \textstyle p_i(\boldsymbol,\boldsymbol,t) ~\stackrel~ / are called ''m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian Formalism
In physics, Hamiltonian mechanics is a reformulation of Lagrangian mechanics that emerged in 1833. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities \dot q^i used in Lagrangian mechanics with (generalized) ''momenta''. Both theories provide interpretations of classical mechanics and describe the same physical phenomena. Hamiltonian mechanics has a close relationship with geometry (notably, symplectic geometry and Poisson structures) and serves as a link between classical and quantum mechanics. Overview Phase space coordinates (''p'', ''q'') and Hamiltonian ''H'' Let (M, \mathcal L) be a mechanical system with configuration space M and smooth Lagrangian \mathcal L. Select a standard coordinate system (\boldsymbol,\boldsymbol) on M. The quantities \textstyle p_i(\boldsymbol,\boldsymbol,t) ~\stackrel~ / are called ''momenta''. (Also ''generalized momenta'', ''conjugate momenta'', and ''canonical momenta''). For a time instant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Louisiana State University
Louisiana State University and Agricultural and Mechanical College, commonly referred to as Louisiana State University (LSU), is an American Public university, public Land-grant university, land-grant research university in Baton Rouge, Louisiana, United States. The university was founded in 1860 near Pineville, Louisiana, under the name Louisiana State Seminary of Learning & Military Academy. The current LSU main campus was dedicated in 1926 and consists of more than 250 buildings constructed in the style of Renaissance, Italian Renaissance architect Andrea Palladio, occupying a plateau on the banks of the Mississippi River. LSU is the Flagship campus, flagship university of the state of Louisiana, as well as the flagship institution of the Louisiana State University System. In 2021, the university enrolled over 28,000 undergraduate and more than 4,500 graduate students in 14 schools and colleges. It is Carnegie Classification of Institutions of Higher Education, classified ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Juhan Frank
Juhan () is a common Estonian male given name. Given name * Juhan Aare (1948–2021), Estonian journalist and politician *Juhan Aavik (1884–1982), Estonian composer * Juhan Mihkel Ainson (1873–1962), Estonian politician *Juhan af Grann (1944–2023, Heikki Juhani Grann), Finnish film director and producer * Juhan Jaanuson (1894–1967), Estonian statistician and politician * Juhan Jaik (1899–1948), Estonian writer and journalist * Juhan Kalm (1884–1953), Estonian agronomist and politician * Juhan Kikas (1892–1944, also known as Jaan Kikkas), Estonian weightlifter *Juhan Kivirähk (born 1957), Estonian sociologist * Juhan Kreem (born 1971), Estonian historian, writer, and archivist * Juhan Kukk (1885–1942), Estonian politician * Juhan Kunder (1852–1888), Estonian writer * Juhan Kurvits (1895–1939), Estonian politician * Juhan Lasn (1861–1930), Estonian politician * Juhan Leeman (1872-19??), Estonian politician and educator * Juhan Leinberg (1812–1885), Estonian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |