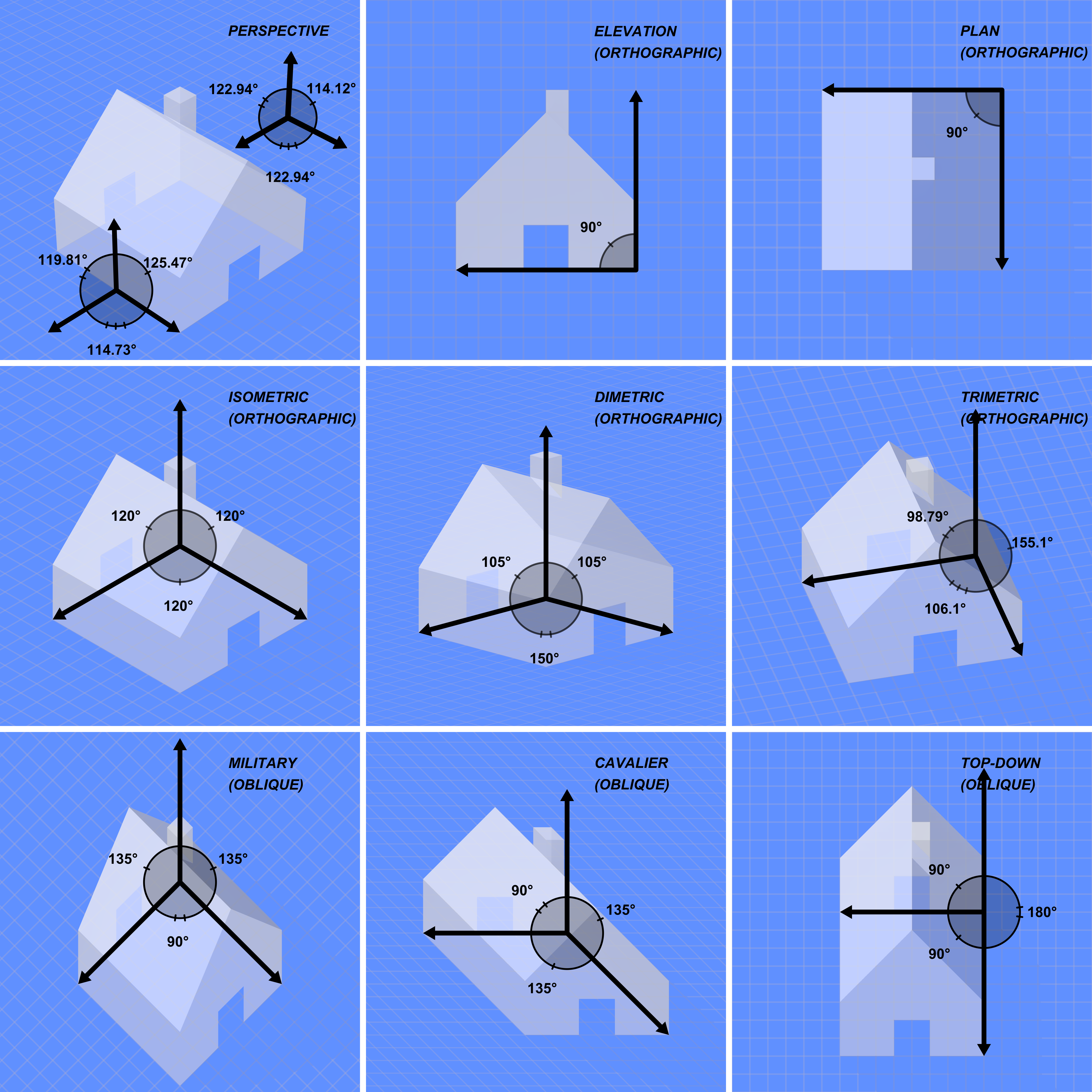
|
Tetraview
A tetraview is an attempt to graph a complex function of a complex variable, by a method invented by Davide P. Cervone. A graph of a real function of a real variable is the set of ordered pairs (x,y) such that y = f(x). This is the ordinary two-dimensional Cartesian graph studied in school algebra. Every complex number has both a real part and an imaginary part, so one complex variable is two-dimensional and a pair of complex variables is four-dimensional. A tetraview is an attempt to give a picture of a four-dimensional object using a two-dimensional representation—either on a piece of paper or on a computer screen, showing a still picture consisting of five views, one in the center and one at each corner. This is roughly analogous to a picture of a three-dimensional object by giving a front view, a side view, and a view from above. A picture of a three-dimensional object is a projection of that object from three dimensions into two dimensions. A tetraview is set of five p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Of A Function
In mathematics, the graph of a function f is the set of ordered pairs (x, y), where f(x) = y. In the common case where x and f(x) are real numbers, these pairs are Cartesian coordinates of points in two-dimensional space and thus form a subset of this plane. In the case of functions of two variables, that is functions whose domain consists of pairs (x, y), the graph usually refers to the set of ordered triples (x, y, z) where f(x,y) = z, instead of the pairs ((x, y), z) as in the definition above. This set is a subset of three-dimensional space; for a continuous real-valued function of two real variables, it is a surface. In science, engineering, technology, finance, and other areas, graphs are tools used for many purposes. In the simplest case one variable is plotted as a function of another, typically using rectangular axes; see '' Plot (graphics)'' for details. A graph of a function is a special case of a relation. In the modern foundations of mathematics, and, typicall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Of A Function Of Two Variables
In mathematics, the graph of a function f is the set of ordered pairs (x, y), where f(x) = y. In the common case where x and f(x) are real numbers, these pairs are Cartesian coordinates of points in two-dimensional space and thus form a subset of this plane. In the case of functions of two variables, that is functions whose domain consists of pairs (x, y), the graph usually refers to the set of ordered triples (x, y, z) where f(x,y) = z, instead of the pairs ((x, y), z) as in the definition above. This set is a subset of three-dimensional space; for a continuous real-valued function of two real variables, it is a surface. In science, engineering, technology, finance, and other areas, graphs are tools used for many purposes. In the simplest case one variable is plotted as a function of another, typically using rectangular axes; see ''Plot (graphics)'' for details. A graph of a function is a special case of a relation. In the modern foundations of mathematics, and, typicall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Variable
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, applied mathematics; as well as in physics, including the branches of hydrodynamics, thermodynamics, and particularly quantum mechanics. By extension, use of complex analysis also has applications in engineering fields such as nuclear, aerospace, mechanical and electrical engineering. As a differentiable function of a complex variable is equal to its Taylor series (that is, it is analytic), complex analysis is particularly concerned with analytic functions of a complex variable (that is, holomorphic functions). History Complex analysis is one of the classical branches in mathematics, with roots in the 18th century and just prior. Important mathematicians associated with complex numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate Axis
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is significant, and they are sometimes identified by their position in an ordered tuple and sometimes by a letter, as in "the ''x''-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and ''vice versa''; this is the basis of analytic geometry. Common coordinate systems Number line The simplest example of a coordinate system is the identification of points on a line with real numbers using the ''number line''. In this system, an arbitrary point ''O'' (the ''origin'') is chosen on a given line. The coordinate of a po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It may be embedded in 4-dimensional Euclidean space as the set of points equidistant from a fixed central point. Analogous to how the boundary of a ball in three dimensions is an ordinary sphere (or 2-sphere, a two-dimensional surface), the boundary of a ball in four dimensions is a 3-sphere (an object with three dimensions). A 3-sphere is an example of a 3-manifold and an ''n''-sphere. Definition In coordinates, a 3-sphere with center and radius is the set of all points in real, 4-dimensional space () such that :\sum_^3(x_i - C_i)^2 = ( x_0 - C_0 )^2 + ( x_1 - C_1 )^2 + ( x_2 - C_2 )^2+ ( x_3 - C_3 )^2 = r^2. The 3-sphere centered at the origin with radius 1 is called the unit 3-sphere and is usually denoted : :S^3 = \left\. It is often convenient to regard as the space with 2 complex dimensions () or the quaternions (). The unit 3-sphere is then given by :S^3 = \left\ or :S^3 = \left\. This d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets. For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another sphere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3D Projection
A 3D projection (or graphical projection) is a design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane. 3D projections use the primary qualities of an object's basic shape to create a map of points, that are then connected to one another to create a visual element. The result is a graphic that contains conceptual properties to interpret that the figure or image as not actually flat (2D), but rather, as a solid object (3D) being viewed on a 2D display. 3D objects are largely displayed on two-dimensional mediums (i.e. paper and computer monitors). As such, graphical projections are a commonly used design element; notably, in engineering drawing, drafting, and computer graphics. Projections can be calculated through employment of mathematical analysis and formulae, or by using various geometric and o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Imaginary Part
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Part
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics. Elementary algebra deals with the manipulation of variables (commonly represented by Roman letters) as if they were numbers and is therefore essential in all applications of mathematics. Abstract algebra is the name given, mostly in education, to the study of algebraic structures such as groups, rings, and fields (the term is no more in common use outside educational context). Linear algebra, which deals with linear equations and linear mappings, is used for modern presentations of geometry, and has many practical applications (in weather forecasting, for example). There are many areas of mathematics that belong to algebra, some having "algebra" in their name, such as commutative algebra, and some not, such as Galois theory. The word ''algebra'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Davide P
Davide is an Italian given name (common) and an Italian/Filipino surname (relatively rare), and may refer to: Given name * Davide Alviti (born 1996), Italian basketball player * Davide Ancilotto (1974–1997), Italian basketball player * Davide Astori (1987-2018), Italian footballer * Davide Biale (born 1994), Italian Bass Slapper * Davide Dias (born 1983), a Portuguese footballer * Davide Faraone (born 1975), Italian politician * Davide Faraoni (born 1991), Italian footballer * Davide Lorenzini (born 1969), Italian diver * Davide Nicola (born 1973), former Italian footballer and manager * Davide Sanguinetti (born 1972), Italian former tennis player * Davide Valsecchi (born 1987), Italian racing driver * Davide Santon (born 1991) Italian footballer Surname *Hilario Davide Jr. (born 1935), Philippine chief justice *Hilario Davide III (born 1964), Filipino politician See also *David (other) David was the second king of the United Kingdom of Israel and a figure in the scrip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Tetrahedron")
