|
Temperature Reference Point
Scale of temperature is a methodology of calibrating the physical quantity temperature in metrology. Empirical scales measure temperature in relation to convenient and stable parameters or reference points, such as the freezing and boiling point of water. Absolute temperature is based on thermodynamic principles: using the lowest possible temperature as the zero point, and selecting a convenient incremental unit. Celsius, Kelvin, and Fahrenheit are common temperature scales. Other scales used throughout history include Rankine, Rømer, Newton, Delisle, Réaumur, Gas mark, Leiden, and Wedgwood. Technical definition The zeroth law of thermodynamics describes thermal equilibrium between thermodynamic systems in form of an equivalence relation. Accordingly, the set of all thermal systems may be divided into a quotient set of equivalence classes, denoted as M, where any element of M collects all systems that are in thermal equilibrium with one another. If the set M has cardina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Quantity
A physical quantity (or simply quantity) is a property of a material or system that can be Quantification (science), quantified by measurement. A physical quantity can be expressed as a ''value'', which is the algebraic multiplication of a ''numerical value'' and a ''unit of measurement''. For example, the physical quantity mass, symbol ''m'', can be quantified as ''m'n''kg, where ''n'' is the numerical value and kg is the unit symbol (for kilogram). Quantities that are vectors have, besides numerical value and unit, direction or orientation in space. Components Following ISO 80000-1, any value or Magnitude (mathematics), magnitude of a physical quantity is expressed as a comparison to a unit of that quantity. The ''value'' of a physical quantity ''Z'' is expressed as the product of a ''numerical value'' (a pure number) and a unit [''Z'']: :Z = \ \times [Z] For example, let Z be "2 metres"; then, \ = 2 is the numerical value and [Z] = \mathrm is the unit. Conversely, the nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gas Mark
The gas mark is a temperature scale used on gas ovens and cookers in the United Kingdom, Republic of Ireland, Ireland and some Commonwealth of Nations countries. History Early gas ovens had no thermostats and it was up to the cook to continually adjust a manual valve to keep the oven at the desired temperature. For this and other reasons gas cookers were not popular; most users preferred the coal-fired open kitchen range. The breakthrough came in the 1920s when a manufacturer introduced the Regulo. REGULO was originally a proprietary name chosen by Radiation Ltd. to denote their new automatic temperature controller. In a series of press advertisements published on 13 May 1923 to announce their "New World" cooker it was stated that, by simply setting a pointer, the oven would go to the desired temperature and stay there without requiring further attention. The current (2025) online edition of the ''Oxford English Dictionary'' indicates that Radiation Ltd. applied to register ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Temperature
Thermodynamic temperature, also known as absolute temperature, is a physical quantity which measures temperature starting from absolute zero, the point at which particles have minimal thermal motion. Thermodynamic temperature is typically expressed using the Kelvin scale, where the unit of measurement is the ''kelvin'' (unit symbol: K). The Kelvin scale uses the same degree interval as the Celsius scale but is offset so that 0 K corresponds to absolute zero. For comparison, a temperature of 295 K corresponds to 21.85 °C and 71.33 °F. Another absolute scale of temperature is the Rankine scale, which is based on the Fahrenheit degree interval. Historically, thermodynamic temperature was defined by Lord Kelvin in terms of a macroscopic relation between Work (thermodynamics), thermodynamic work and Heat, heat transfer as defined in thermodynamics, but the kelvin was redefined by international agreement in 2019 in terms of phenomena that are now understood as man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
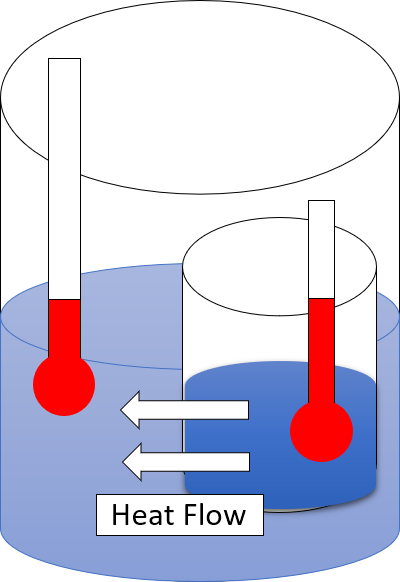
Second Law Of Thermodynamics
The second law of thermodynamics is a physical law based on Universal (metaphysics), universal empirical observation concerning heat and Energy transformation, energy interconversions. A simple statement of the law is that heat always flows spontaneously from hotter to colder regions of matter (or 'downhill' in terms of the temperature gradient). Another statement is: "Not all heat can be converted into Work (thermodynamics), work in a cyclic process."Young, H. D; Freedman, R. A. (2004). ''University Physics'', 11th edition. Pearson. p. 764. The second law of thermodynamics establishes the concept of entropy as a physical property of a thermodynamic system. It predicts whether processes are forbidden despite obeying the requirement of conservation of energy as expressed in the first law of thermodynamics and provides necessary criteria for spontaneous processes. For example, the first law allows the process of a cup falling off a table and breaking on the floor, as well as allowi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Injective Function
In mathematics, an injective function (also known as injection, or one-to-one function ) is a function that maps distinct elements of its domain to distinct elements of its codomain; that is, implies (equivalently by contraposition, implies ). In other words, every element of the function's codomain is the image of one element of its domain. The term must not be confused with that refers to bijective functions, which are functions such that each element in the codomain is an image of exactly one element in the domain. A homomorphism between algebraic structures is a function that is compatible with the operations of the structures. For all common algebraic structures, and, in particular for vector spaces, an is also called a . However, in the more general context of category theory, the definition of a monomorphism differs from that of an injective homomorphism. This is thus a theorem that they are equivalent for algebraic structures; see for more details. A func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuum (set Theory)
In the mathematical field of set theory, the continuum means the real numbers, or the corresponding (infinite) cardinal number, denoted by \mathfrak. Georg Cantor proved that the cardinality \mathfrak is larger than the smallest infinity, namely, \aleph_0. He also proved that \mathfrak is equal to 2^\!, the cardinality of the power set of the natural numbers. The ''cardinality of the continuum'' is the size of the set of real numbers. The continuum hypothesis is sometimes stated by saying that no cardinality lies between that of the continuum and that of the natural numbers, \aleph_0, or alternatively, that \mathfrak = \aleph_1. Linear continuum According to Raymond Wilder (1965), there are four axioms that make a set ''C'' and the relation < into a linear continuum: * ''C'' is simply ordered with respect to <. * If [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardinality
The thumb is the first digit of the hand, next to the index finger. When a person is standing in the medical anatomical position (where the palm is facing to the front), the thumb is the outermost digit. The Medical Latin English noun for thumb is ''pollex'' (compare ''hallux'' for big toe), and the corresponding adjective for thumb is ''pollical''. Definition Thumb and fingers The English word ''finger'' has two senses, even in the context of appendages of a single typical human hand: 1) Any of the five terminal members of the hand. 2) Any of the four terminal members of the hand, other than the thumb. Linguistically, it appears that the original sense was the first of these two: (also rendered as ) was, in the inferred Proto-Indo-European language, a suffixed form of (or ), which has given rise to many Indo-European-family words (tens of them defined in English dictionaries) that involve, or stem from, concepts of fiveness. The thumb shares the following with each of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivalence Class
In mathematics, when the elements of some set S have a notion of equivalence (formalized as an equivalence relation), then one may naturally split the set S into equivalence classes. These equivalence classes are constructed so that elements a and b belong to the same equivalence class if, and only if, they are equivalent. Formally, given a set S and an equivalence relation \sim on S, the of an element a in S is denoted /math> or, equivalently, to emphasize its equivalence relation \sim, and is defined as the set of all elements in S with which a is \sim-related. The definition of equivalence relations implies that the equivalence classes form a partition of S, meaning, that every element of the set belongs to exactly one equivalence class. The set of the equivalence classes is sometimes called the quotient set or the quotient space of S by \sim, and is denoted by S /. When the set S has some structure (such as a group operation or a topology) and the equivalence re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivalence Relation
In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric, and transitive. The equipollence relation between line segments in geometry is a common example of an equivalence relation. A simpler example is equality. Any number a is equal to itself (reflexive). If a = b, then b = a (symmetric). If a = b and b = c, then a = c (transitive). Each equivalence relation provides a partition of the underlying set into disjoint equivalence classes. Two elements of the given set are equivalent to each other if and only if they belong to the same equivalence class. Notation Various notations are used in the literature to denote that two elements a and b of a set are equivalent with respect to an equivalence relation R; the most common are "a \sim b" and "", which are used when R is implicit, and variations of "a \sim_R b", "", or "" to specify R explicitly. Non-equivalence may be written "" or "a \not\equiv b". Definitions A binary relation \,\si ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic System
A thermodynamic system is a body of matter and/or radiation separate from its surroundings that can be studied using the laws of thermodynamics. Thermodynamic systems can be passive and active according to internal processes. According to internal processes, passive systems and active systems are distinguished: passive, in which there is a redistribution of available energy, active, in which one type of energy is converted into another. Depending on its interaction with the environment, a thermodynamic system may be an isolated system, a Closed system#In thermodynamics, closed system, or an Open system (systems theory), open system. An isolated system does not exchange matter or energy with its surroundings. A closed system may exchange heat, experience forces, and exert forces, but does not exchange matter. An open system can interact with its surroundings by exchanging both matter and energy. The physical condition of a thermodynamic system at a given time is described by its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |