|
Subtypes
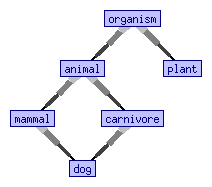
In programming language theory, subtyping (also subtype polymorphism or inclusion polymorphism) is a form of type polymorphism in which a subtype is a datatype that is related to another datatype (the supertype) by some notion of substitutability, meaning that program elements, typically subroutines or functions, written to operate on elements of the supertype can also operate on elements of the subtype. If S is a subtype of T, the subtyping relation (written as , , or ) means that any term of type S can ''safely be used'' in ''any context'' where a term of type T is expected. The precise semantics of subtyping here crucially depends on the particulars of how ''"safely be used"'' and ''"any context"'' are defined by a given type formalism or programming language. The type system of a programming language essentially defines its own subtyping relation, which may well be trivial, should the language support no (or very little) conversion mechanisms. Due to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Datatype
In computer science and computer programming, a data type (or simply type) is a set of possible values and a set of allowed operations on it. A data type tells the compiler or interpreter how the programmer intends to use the data. Most programming languages support basic data types of integer numbers (of varying sizes), floating-point numbers (which approximate real numbers), characters and Booleans. A data type constrains the possible values that an expression, such as a variable or a function, might take. This data type defines the operations that can be done on the data, the meaning of the data, and the way values of that type can be stored. Concept A data type is a collection or grouping of data values. Such a grouping may be defined for many reasons: similarity, convenience, or to focus the attention. It is frequently a matter of good organization that aids the understanding of complex definitions. Almost all programming languages explicitly include the notion of da ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Substitutability
The Liskov substitution principle (LSP) is a particular definition of a subtyping relation, called strong behavioral subtyping, that was initially introduced by Barbara Liskov in a 1988 conference keynote address titled ''Data abstraction and hierarchy''. It is based on the concept of "substitutability" a principle in object-oriented programming stating that an object (such as a class) may be replaced by a sub-object (such as a class that extends the first class) without breaking the program. It is a semantic rather than merely syntactic relation, because it intends to guarantee semantic interoperability of types in a hierarchy, object types in particular. Barbara Liskov and Jeannette Wing described the principle succinctly in a 1994 paper as follows: ''Subtype Requirement'': Let be a property provable about objects of type . Then should be true for objects of type where is a subtype of . Symbolically: :S <: T \to (\forall xT) \phi(x) \to (\forall yS) \phi(y) T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Liskov Substitution Principle
The Liskov substitution principle (LSP) is a particular definition of a subtyping relation, called strong behavioral subtyping, that was initially introduced by Barbara Liskov in a 1988 conference keynote address titled ''Data abstraction and hierarchy''. It is based on the concept of "substitutability" a principle in object-oriented programming stating that an object (such as a class) may be replaced by a sub-object (such as a class that extends the first class) without breaking the program. It is a semantic rather than merely syntactic relation, because it intends to guarantee semantic interoperability of types in a hierarchy, object types in particular. Barbara Liskov and Jeannette Wing described the principle succinctly in a 1994 paper as follows: ''Subtype Requirement'': Let be a property provable about objects of type . Then should be true for objects of type where is a subtype of . Symbolically: :S <: T \to (\forall xT) \phi(x) \to (\forall yS) \phi(y) T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Type System
In computer programming, a type system is a logical system comprising a set of rules that assigns a property called a type to every "term" (a word, phrase, or other set of symbols). Usually the terms are various constructs of a computer program, such as variables, expressions, functions, or modules. A type system dictates the operations that can be performed on a term. For variables, the type system determines the allowed values of that term. Type systems formalize and enforce the otherwise implicit categories the programmer uses for algebraic data types, data structures, or other components (e.g. "string", "array of float", "function returning boolean"). Type systems are often specified as part of programming languages and built into interpreters and compilers, although the type system of a language can be extended by optional tools that perform added checks using the language's original type syntax and grammar. The main purpose of a type system in a programming langua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polymorphism (computer Science)
In programming language theory and type theory, polymorphism is the provision of a single interface (computing), interface to entities of different Data type, types or the use of a single symbol to represent multiple different types.: "Polymorphic types are types whose operations are applicable to values of more than one type." The concept is borrowed from a principle in biology where an organism or species can have many different forms or stages. The most commonly recognized major classes of polymorphism are: * ''Ad hoc polymorphism'': defines a common interface for an arbitrary set of individually specified types. * ''Parametric polymorphism'': not specifying concrete types and instead use abstract symbols that can substitute for any type. * ''Subtyping'' (also called ''subtype polymorphism'' or ''inclusion polymorphism''): when a name denotes instances of many different classes related by some common superclass. History Interest in polymorphic type systems developed significa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bounded Quantification
In type theory, bounded quantification (also bounded polymorphism or constrained genericity) refers to universal or existential quantifiers which are restricted ("bounded") to range only over the subtypes of a particular type. Bounded quantification is an interaction of parametric polymorphism with subtyping. Bounded quantification has traditionally been studied in the functional setting of System F<:, but is available in modern object-oriented languages supporting parametric polymorphism () such as [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Record (computer Science)
In computer science, a record (also called a structure, struct (C programming language), struct, or compound data) is a basic data structure. Records in a database or spreadsheet are usually called "row (database), rows". A record is a collection of ''Field (computer science), fields'', possibly of different data types, typically in a fixed number and sequence. The fields of a record may also be called ''members'', particularly in object-oriented programming; fields may also be called ''elements'', though this risks confusion with the elements of a Collection (abstract data type), collection. For example, a date could be stored as a record containing a numeric year field, a month field represented as a string, and a numeric day-of-month field. A personnel record might contain a name, a salary, and a rank. A Circle record might contain a center and a radius—in this instance, the center itself might be represented as a point record containing x and y coordinates. Records are dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Programming Language Theory
Programming language theory (PLT) is a branch of computer science that deals with the design, implementation, analysis, characterization, and classification of formal languages known as programming languages. Programming language theory is closely related to other fields including mathematics, software engineering, and linguistics. There are a number of academic conferences and journals in the area. History In some ways, the history of programming language theory predates even the development of programming languages themselves. The lambda calculus, developed by Alonzo Church and Stephen Cole Kleene in the 1930s, is considered by some to be the world's first programming language, even though it was intended to ''model'' computation rather than being a means for programmers to ''describe'' algorithms to a computer system. Many modern functional programming languages have been described as providing a "thin veneer" over the lambda calculus, and many are easily described in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inheritance (computer Science)
In object-oriented programming, inheritance is the mechanism of basing an object or class upon another object ( prototype-based inheritance) or class ( class-based inheritance), retaining similar implementation. Also defined as deriving new classes ( sub classes) from existing ones such as super class or base class and then forming them into a hierarchy of classes. In most class-based object-oriented languages, an object created through inheritance, a "child object", acquires all the properties and behaviors of the "parent object" , with the exception of: constructors, destructor, overloaded operators and friend functions of the base class. Inheritance allows programmers to create classes that are built upon existing classes, to specify a new implementation while maintaining the same behaviors ( realizing an interface), to reuse code and to independently extend original software via public classes and interfaces. The relationships of objects or classes through inheritance give ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Order-sorted Logic
Many-sorted logic can reflect formally our intention not to handle the universe as a homogeneous collection of objects, but to partition it in a way that is similar to types in typeful programming. Both functional and assertive "parts of speech" in the language of the logic reflect this typeful partitioning of the universe, even on the syntax level: substitution and argument passing can be done only accordingly, respecting the "sorts". There are various ways to formalize the intention mentioned above; a ''many-sorted logic'' is any package of information which fulfils it. In most cases, the following are given: * a set of sorts, ''S'' * an appropriate generalization of the notion of ''signature'' to be able to handle the additional information that comes with the sorts. The domain of discourse of any structure of that signature is then fragmented into disjoint subsets, one for every sort. Example When reasoning about biological organisms, it is useful to distinguish two sorts: \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category Theory
Category theory is a general theory of mathematical structures and their relations that was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Nowadays, category theory is used in almost all areas of mathematics, and in some areas of computer science. In particular, many constructions of new mathematical objects from previous ones, that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient spaces, direct products, completion, and duality. A category is formed by two sorts of objects: the objects of the category, and the morphisms, which relate two objects called the ''source'' and the ''target'' of the morphism. One often says that a morphism is an ''arrow'' that ''maps'' its source to its target. Morphisms can be ''composed'' if the target of the first morphism equals the source of the second one, and morphism com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simula
Simula is the name of two simulation programming languages, Simula I and Simula 67, developed in the 1960s at the Norwegian Computing Center in Oslo, by Ole-Johan Dahl and Kristen Nygaard. Syntactically, it is an approximate superset of ALGOL 60, and was also influenced by the design of Simscript. Simula 67 introduced objects, classes, inheritance and subclasses, virtual procedures, coroutines, and discrete event simulation, and featured garbage collection. Other forms of subtyping (besides inheriting subclasses) were introduced in Simula derivatives. Simula is considered the first object-oriented programming language. As its name suggests, the first Simula version by 1962 was designed for doing simulations; Simula 67 though was designed to be a general-purpose programming language and provided the framework for many of the features of object-oriented languages today. Simula has been used in a wide range of applications such as simulating very-large-scale integrati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |