|
Snub (geometry)
In geometry, a snub is an operation applied to a polyhedron. The term originates from Kepler's names of two Archimedean solids, for the snub cube () and snub dodecahedron (). In general, snubs have chiral symmetry with two forms: with clockwise or counterclockwise orientation. By Kepler's names, a snub can be seen as an expansion of a regular polyhedron: moving the faces apart, twisting them about their centers, adding new polygons centered on the original vertices, and adding pairs of triangles fitting between the original edges. The terminology was generalized by Coxeter, with a slightly different definition, for a wider set of uniform polytopes. Conway snubs John Conway explored generalized polyhedron operators, defining what is now called Conway polyhedron notation, which can be applied to polyhedra and tilings. Conway calls Coxeter's operation a ''semi-snub''. In this notation, snub is defined by the dual and gyro operators, as ''s'' = ''dg'', and it is e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedean Solid
In geometry, an Archimedean solid is one of the 13 solids first enumerated by Archimedes. They are the convex uniform polyhedra composed of regular polygons meeting in identical vertices, excluding the five Platonic solids (which are composed of only one type of polygon), excluding the prisms and antiprisms, and excluding the pseudorhombicuboctahedron. They are a subset of the Johnson solids, whose regular polygonal faces do not need to meet in identical vertices. "Identical vertices" means that each two vertices are symmetric to each other: A global isometry of the entire solid takes one vertex to the other while laying the solid directly on its initial position. observed that a 14th polyhedron, the elongated square gyrobicupola (or pseudo-rhombicuboctahedron), meets a weaker definition of an Archimedean solid, in which "identical vertices" means merely that the faces surrounding each vertex are of the same types (i.e. each vertex looks the same from close up), so only a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Horton Conway
John Horton Conway (26 December 1937 – 11 April 2020) was an English mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many branches of recreational mathematics, most notably the invention of the cellular automaton called the Game of Life. Born and raised in Liverpool, Conway spent the first half of his career at the University of Cambridge before moving to the United States, where he held the John von Neumann Professorship at Princeton University for the rest of his career. On 11 April 2020, at age 82, he died of complications from COVID-19. Early life and education Conway was born on 26 December 1937 in Liverpool, the son of Cyril Horton Conway and Agnes Boyce. He became interested in mathematics at a very early age. By the time he was 11, his ambition was to become a mathematician. After leaving sixth form, he studied mathematics at Gonville and Caius College, Ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Tiling
In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of English mathematician John Conway called it a deltille, named from the triangular shape of the Greek letter delta (Δ). The triangular tiling can also be called a kishextille by a kis operation that adds a center point and triangles to replace the faces of a hextille. It is one of three regular tilings of the plane. The other two are the square tiling and the hexagonal tiling. Uniform colorings There are 9 distinct uniform colorings of a triangular tiling. (Naming the colors by indices on the 6 triangles around a vertex: 111111, 111112, 111212, 111213, 111222, 112122, 121212, 121213, 121314) Three of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagonal Tiling
In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of or (as a truncated triangular tiling). English mathematician John Conway called it a hextille. The internal angle of the hexagon is 120 degrees, so three hexagons at a point make a full 360 degrees. It is one of three regular tilings of the plane. The other two are the triangular tiling and the square tiling. Applications The hexagonal tiling is the densest way to arrange circles in two dimensions. The honeycomb conjecture states that the hexagonal tiling is the best way to divide a surface into regions of equal area with the least total perimeter. The optimal three-dimensional structure for making honeycomb (or rather, soap bubbles) was investigated by Lord Kelvin, who believed that the Kelvin structure (or body-centered cubic lattice) is optimal. However, the less regular Weaire� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Tiling
In geometry, the square tiling, square tessellation or square grid is a regular tiling of the Euclidean plane. It has Schläfli symbol of meaning it has 4 squares around every vertex. Conway called it a quadrille. The internal angle of the square is 90 degrees so four squares at a point make a full 360 degrees. It is one of three regular tilings of the plane. The other two are the triangular tiling and the hexagonal tiling. Uniform colorings There are 9 distinct uniform colorings of a square tiling. Naming the colors by indices on the 4 squares around a vertex: 1111, 1112(i), 1112(ii), 1122, 1123(i), 1123(ii), 1212, 1213, 1234. (i) cases have simple reflection symmetry, and (ii) glide reflection symmetry. Three can be seen in the same symmetry domain as reduced colorings: 1112i from 1213, 1123i from 1234, and 1112ii reduced from 1123ii. Related polyhedra and tilings This tiling is topologically related as a part of sequence of regular polyhedra and tilings, extend ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecahedron
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along with the rhombic dodecahedra, are space-filling. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons". There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical than others. The best known is the ( convex, non- stellated) regular icosahedron—one of the Platonic solids—whose faces are 20 equilateral triangles. Regular icosahedra There are two objects, one convex and one nonconvex, that can both be called regular icosahedra. Each has 30 edges and 20 equilateral triangle faces with five meeting at each of its twelve vertices. Both have icosahedral symmetry. The term "regular icosahedron" generally refers to the convex variety, while the nonconvex form is called a ''great icosahedron''. Convex regular icosahedron The convex regular icosahedron is usually referred to simply as the ''regular icosahedron'', one of the five regular Platonic solids, and is represented by its Schläfli symbol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedron
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. A regular octahedron is the dual polyhedron of a cube. It is a rectified tetrahedron. It is a square bipyramid in any of three orthogonal orientations. It is also a triangular antiprism in any of four orientations. An octahedron is the three-dimensional case of the more general concept of a cross polytope. A regular octahedron is a 3-ball in the Manhattan () metric. Regular octahedron Dimensions If the edge length of a regular octahedron is ''a'', the radius of a circumscribed sphere (one that touches the octahedron at all vertices) is :r_u = \frac a \approx 0.707 \cdot a and the radius of an inscribed sphere (tangent to each of the octahedron's faces) is :r_i = \frac a \approx 0.408\cdot a while the midradius, which t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only regular hexahedron and is one of the five Platonic solids. It has 6 faces, 12 edges, and 8 vertices. The cube is also a square parallelepiped, an equilateral cuboid and a right rhombohedron a 3-zonohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations. The cube is dual to the octahedron. It has cubical or octahedral symmetry. The cube is the only convex polyhedron whose faces are all squares. Orthogonal projections The ''cube'' has four special orthogonal projections, centered, on a vertex, edges, face and normal to its vertex figure. The first and third correspond to the A2 and B2 Coxeter planes. Spherical tiling The cube can also be represented as a spherical tiling, and p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets. For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and anot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
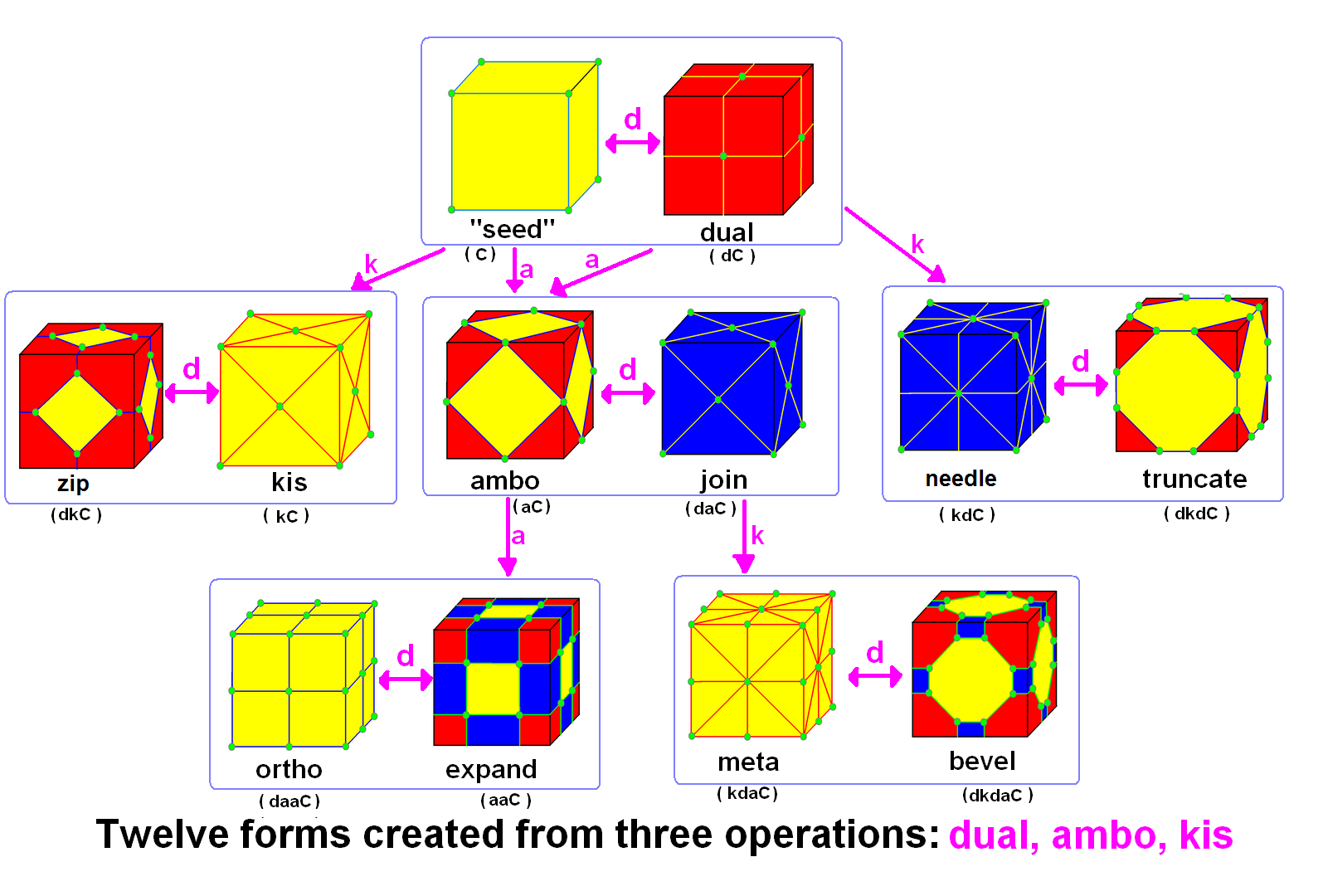
Conway Ambo Operator
In geometry, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations. Conway and Hart extended the idea of using operators, like truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, represents a truncated cube, and , parsed as , is ( topologically) a truncated cuboctahedron. The simplest operator dual swaps vertex and face elements; e.g., a dual cube is an octahedron: . Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators (ambo), ( bevel), ( dual), (expand), (gyro), (join), (kis), (meta), (ortho), (snub), and (truncate), while Hart added ( reflect) and (propellor). Later implementations named further operators, sometimes referred to as "extended" operators. Conway's basic operations are sufficient to generate the Archimedean and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternation (geometry)
In geometry, an alternation or ''partial truncation'', is an operation on a polygon, polyhedron, tiling, or higher dimensional polytope that removes alternate vertices.Coxeter, Regular polytopes, pp. 154–156 8.6 Partial truncation, or alternation Coxeter labels an ''alternation'' by a prefixed ''h'', standing for ''hemi'' or ''half''. Because alternation reduces all polygon faces to half as many sides, it can only be applied to polytopes with all even-sided faces. An alternated square face becomes a digon, and being degenerate, is usually reduced to a single edge. More generally any vertex-uniform polyhedron or tiling with a vertex configuration consisting of all even-numbered elements can be ''alternated''. For example, the alternation of a vertex figure with ''2a.2b.2c'' is ''a.3.b.3.c.3'' where the three is the number of elements in this vertex figure. A special case is square faces whose order divides in half into degenerate digons. So for example, the cube ''4.4 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |





.jpg)