|
Sinusoidal Plane Wave
In physics, a sinusoidal (or monochromatic) plane wave is a special case of plane wave: a field whose value varies as a sinusoidal function of time and of the distance from some fixed plane. For any position \vec x in space and any time t, the value of such a field can be written as :F(\vec x, t)=A \cos\left(2\pi \nu (\vec x \cdot \vec n - c t) + \varphi\right)\, where \vec n is a unit-length vector, the direction of propagation of the wave, and "\cdot" denotes the dot product of two vectors. The parameter A, which may be a scalar or a vector, is called the amplitude of the wave; the coefficient \nu, a positive scalar, its spatial frequency; and the adimensional scalar \varphi, an angle in radians, is its initial phase or phase shift. The scalar quantity d = \vec x \cdot \vec n gives the (signed) displacement of the point \vec x from the plane that is perpendicular to \vec n and goes through the origin of the coordinate system. This quantity is constant over each plane perpendic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
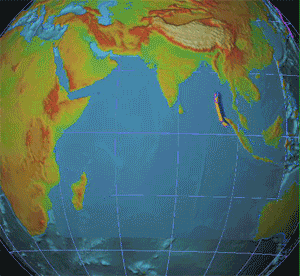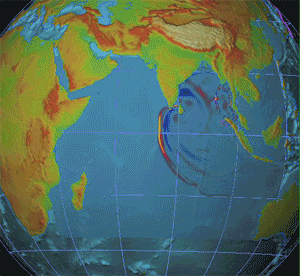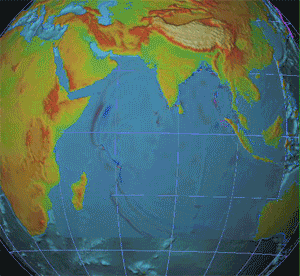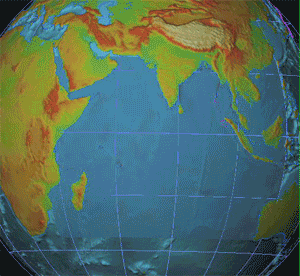
Seismology
Seismology (; from Ancient Greek σεισμός (''seismós'') meaning "earthquake" and -λογία (''-logía'') meaning "study of") is the scientific study of earthquakes and the propagation of elastic waves through the Earth or through other planet-like bodies. It also includes studies of earthquake environmental effects such as tsunamis as well as diverse seismic sources such as volcanic, tectonic, glacial, fluvial, oceanic, atmospheric, and artificial processes such as explosions. A related field that uses geology to infer information regarding past earthquakes is paleoseismology. A recording of Earth motion as a function of time is called a seismogram. A seismologist is a scientist who does research in seismology. History Scholarly interest in earthquakes can be traced back to antiquity. Early speculations on the natural causes of earthquakes were included in the writings of Thales of Miletus (c. 585 BCE), Anaximenes of Miletus (c. 550 BCE), Aristotle (c. 340 BCE), and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Base (exponentiation)
In exponentiation, the base is the number b in an expression of the form bn. Related terms The number n is called the exponent and the expression is known formally as exponentiation of b by n or the exponential of n with base b. It is more commonly expressed as "the nth power of b", "b to the nth power" or "b to the power n". For example, the fourth power of 10 is 10,000 because . The term ''power'' strictly refers to the entire expression, but is sometimes used to refer to the exponent. Radix is the traditional term for ''base'', but usually refers then to one of the common bases: decimal (10), binary (2), hexadecimal (16), or sexagesimal (60). When the concepts of variable and constant came to be distinguished, the process of exponentiation was seen to transcend the algebraic functions. In his 1748 ''Introductio in analysin infinitorum'', Leonhard Euler referred to "base a = 10" in an example. He referred to ''a'' as a "constant number" in an extensive consideration of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Exponential
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the notion of exponentiation (repeated multiplication), but modern definitions (there are several equivalent characterizations) allow it to be rigorously extended to all real arguments, including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to opine that the exponential function is "the most important function in mathematics". The exponential function satisfies the exponentiation identity e^ = e^x e^y \text x,y\in\mathbb, which, along with the definition e = \exp(1), shows that e^n=\underbrace_ for positive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Vector
In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength), and its direction is perpendicular to the wavefront. In isotropic media, this is also the direction of wave propagation. A closely related vector is the angular wave vector (or angular wavevector), with a typical unit being radian per metre. The wave vector and angular wave vector are related by a fixed constant of proportionality, 2π radians per cycle. It is common in several fields of physics to refer to the angular wave vector simply as the ''wave vector'', in contrast to, for example, crystallography. It is also common to use the symbol ''k'' for whichever is in use. In the context of special relativity, ''wave vector'' can refer to a four-vector, in which the (angular) wave vector and (angular) frequency are combined. Def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Frequency
In physics, angular frequency "''ω''" (also referred to by the terms angular speed, circular frequency, orbital frequency, radian frequency, and pulsatance) is a scalar measure of rotation rate. It refers to the angular displacement per unit time (for example, in rotation) or the rate of change of the phase of a sinusoidal waveform (for example, in oscillations and waves), or as the rate of change of the argument of the sine function. Angular frequency (or angular speed) is the magnitude of the pseudovector quantity angular velocity.(UP1) One turn is equal to 2''π'' radians, hence \omega = \frac = , where: *''ω'' is the angular frequency (unit: radians per second), *''T'' is the period (unit: seconds), *''f'' is the ordinary frequency (unit: hertz) (sometimes ''ν''). Units In SI units, angular frequency is normally presented in radians per second, even when it does not express a rotational value. The unit hertz (Hz) is dimensionally equivalent, but by conventi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Period (physics)
Period may refer to: Common uses * Era, a length or span of time * Full stop (or period), a punctuation mark Arts, entertainment, and media * Period (music), a concept in musical composition * Periodic sentence (or rhetorical period), a concept in grammar and literary style. * Period, a descriptor for a historical or period drama * Period, a timeframe in which a particular style of antique furniture or some other work of art was produced, such as the "Edwardian period" * '' Period (Another American Lie)'', a 1987 album by B.A.L.L. * ''Period'' (mixtape), a 2018 mixtape by City Girls * ''Period'', the final book in Dennis Cooper's George Miles cycle of novels Mathematics * In a repeating decimal, the length of the repetend * Period of a function, length or duration after which a function repeats itself * Period (algebraic geometry), numbers that can be expressed as integrals of algebraic differential forms over algebraically defined domains, forming a ring Science * Perio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane Wave 3D Animation 300x216 255Colors
Plane(s) most often refers to: * Aero- or airplane, a powered, fixed-wing aircraft * Plane (geometry), a flat, 2-dimensional surface Plane or planes may also refer to: Biology * Plane (tree) or ''Platanus'', wetland native plant * ''Planes'' (genus), marsh crabs in Grapsidae * ''Bindahara phocides'', the plane butterfly of Asia Maritime transport * Planing (boat), where weight is predominantly supported by hydrodynamic lift * ''Plane'' (wherry), a Norfolk canal boat, in use 1931–1949 Music *"Planes", a 1976 song by Colin Blunstone *"Planes (Experimental Aircraft)", a 1989 song by Jefferson Airplane from '' Jefferson Airplane'' *"Planez", originally "Planes", a 2015 song by Jeremih *"The Plane", a 1987 song on the ''Empire of the Sun'' soundtrack *"The Plane", a 1997 song by Kinito Méndez Other entertainment * Plane (''Dungeons & Dragons''), any fictional realm of the D&D roleplaying game's multiverse * ''Planes'' (film), a 2013 animation **'' Planes: Fire & Rescue'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Sinusoidal Cosine Wave Sine Blue
In physics, mathematics, and related fields, a wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities. Waves can be periodic, in which case those quantities oscillate repeatedly about an equilibrium (resting) value at some frequency. When the entire waveform moves in one direction, it is said to be a ''traveling wave''; by contrast, a pair of superimposed periodic waves traveling in opposite directions makes a '' standing wave''. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even zero. Waves are often described by a ''wave equation'' (standing wave field of two opposite waves) or a one-way wave equation for single wave propagation in a defined direction. Two types of waves are most commonly studied in classical physics. In a ''mechanical wave'', stress and strain fields oscillate about a mechanical equilibrium. A mechanical wave is a local deformation (strain) i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted simply as \sin \theta and \cos \theta. More generally, the definitions of sine and cosine can be extended to any real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic phenomena such as sound an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |