|
Siamese Method
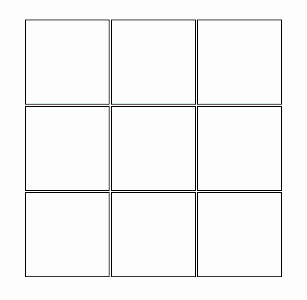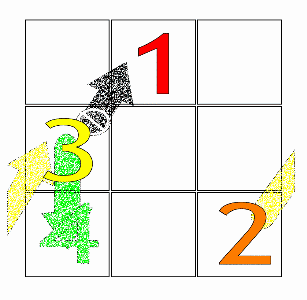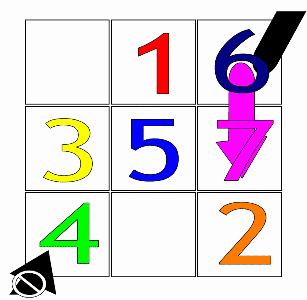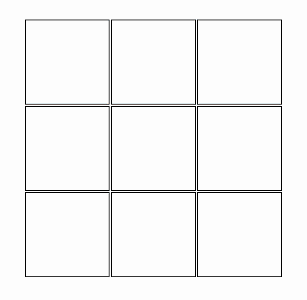
The Siamese method, or De la Loubère method, is a simple method to construct any size of ''n''-odd magic squares (i.e. number squares in which the sums of all rows, columns and diagonals are identical). The method was brought to France in 1688 by the French mathematician and diplomat Simon de la Loubère, as he was returning from his 1687 embassy to the kingdom of Siam. The Siamese method makes the creation of magic squares straightforward. Publication De la Loubère published his findings in his book ''A new historical relation of the kingdom of Siam'' (''Du Royaume de Siam'', 1693), under the chapter entitled ''The problem of the magical square according to the Indians''. Although the method is generally qualified as "Siamese", which refers to de la Loubère's travel to the country of Siam, de la Loubère himself learnt it from a Frenchman named M.Vincent (a doctor, who had first travelled to Persia and then to Siam, and was returning to France with the de la Loubère embass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Claude Gaspard Bachet De Méziriac , a form of brainstem stroke syndrome
{{disambig, geo ...
Claude may refer to: __NOTOC__ People and fictional characters * Claude (given name), a list of people and fictional characters * Claude (surname), a list of people * Claude Lorrain (c. 1600–1682), French landscape painter, draughtsman and etcher traditionally called just "Claude" in English * Madame Claude, French brothel keeper Fernande Grudet (1923–2015) Places * Claude, Texas, a city * Claude, West Virginia, an unincorporated community Other uses * Allied reporting name of the Mitsubishi A5M Japanese carrier-based fighter aircraft * Claude (alligator), an albino alligator at the California Academy of Sciences See also * Claude's syndrome Claude's syndrome is a form of brainstem stroke syndrome characterized by the presence of an ipsilateral oculomotor nerve palsy, contralateral hemiparesis, contralateral ataxia, and contralateral hemiplegia of the lower face, tongue, and shoulder. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strachey Method For Magic Squares
The Strachey method for magic squares is an algorithm for generating magic squares of singly even order 4''k'' + 2. An example of magic square of order 6 constructed with the Strachey method: Strachey's method of construction of singly even magic square of order ''n'' = 4''k'' + 2. 1. Divide the grid into 4 quarters each having ''n''2/4 cells and name them crosswise thus 2. Using the Siamese method (De la Loubère method) complete the individual magic squares of odd order 2''k'' + 1 in subsquares A, B, C, D, first filling up the sub-square A with the numbers 1 to ''n''2/4, then the sub-square B with the numbers ''n''2/4 + 1 to 2''n''2/4,then the sub-square C with the numbers 2''n''2/4 + 1 to 3''n''2/4, then the sub-square D with the numbers 3''n''2/4 + 1 to ''n''2. As a running example, we consider a 10×10 magic square, where we have divided the square into four quarters. The quarter A contains a magic square of numbers from 1 to 25, B a magic square of numbers from 26 to 50 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conway's LUX Method For Magic Squares
Conway's LUX method for magic squares is an algorithm by John Horton Conway for creating magic squares of order 4''n''+2, where ''n'' is a natural number. Method Start by creating a (2''n''+1)-by-(2''n''+1) square array consisting of * ''n''+1 rows of Ls, * 1 row of Us, and * ''n''-1 rows of Xs, and then exchange the U in the middle with the L above it. Each letter represents a 2x2 block of numbers in the finished square. Now replace each letter by four consecutive numbers, starting with 1, 2, 3, 4 in the centre square of the top row, and moving from block to block in the manner of the Siamese method: move up and right, wrapping around the edges, and move down whenever you are obstructed. Fill each 2x2 block according to the order prescribed by the letter: :\mathrm: \quad \begin4&&1\\&\swarrow&\\2&\rightarrow&3\end \qquad \mathrm: \quad \begin1&&4\\\downarrow&&\uparrow\\2&\rightarrow&3\end \qquad \mathrm:\quad \begin1&&4\\&\searrow\!\!\!\!\!\!\nearrow&\\3&&2\end Example Let ''n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johann Faulhaber
Johann Faulhaber (5 May 1580 – 10 September 1635) was a German mathematician. Born in Ulm, Faulhaber was a trained weaver who later took the role of a surveyor of the city of Ulm. He collaborated with Johannes Kepler and Ludolph van Ceulen. Besides his work on the fortifications of cities (notably Basel and Frankfurt), Faulhaber built water wheels in his home town and geometrical instruments for the military. Faulhaber made the first publication of Henry Briggs's Logarithm in Germany. He is also credited with the first printed solution of equal temperament.Date,name,ratio,cents: from equal temperament monochord tables p55-p78; J. Murray Barbour ''Tuning and Temperament'', Michigan State University Press 1951 He died in Ulm. Faulhaber's major contribution was in calculating the sums of powers of integers. Jacob Bernoulli makes references to Faulhaber in his ''Ars Conjectandi''. Works * See also * Faulhaber's formula In mathematics, Faulhaber's formula, named after the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manuel Moschopoulos
Manuel Moschopoulos ( Latinized as Manuel Moschopulus; el, ), was a Byzantine commentator and grammarian, who lived during the end of the 13th and the beginning of the 14th century and was an important figure in the Palaiologan Renaissance. ''Moschopoulos'' means "little calf," and is probably a nickname. Life Moschopoulos was a student of Maximos Planudes and possibly his successor as a head of a school in Constantinople, where he taught throughout his life. A mysterious and ill-documented excursion into politics led to his imprisonment for a while. Works His chief work is ''Erotemata grammaticalia'' (),See Uncial 0135. in the form of question and answer, based upon an anonymous epitome of grammar, and supplemented by a lexicon of Attic nouns. He was also the author of ''scholia'' on the first and second books of the ''Iliad'', on Hesiod, Theocritus, Pindar and other classical and later authors; of riddles, letters, and a treatise on the magic squares. His grammatical treat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reflection (mathematics)
In mathematics, a reflection (also spelled reflexion) is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as a set of fixed points; this set is called the axis (in dimension 2) or plane (in dimension 3) of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection. For example the mirror image of the small Latin letter p for a reflection with respect to a vertical axis would look like q. Its image by reflection in a horizontal axis would look like b. A reflection is an involution: when applied twice in succession, every point returns to its original location, and every geometrical object is restored to its original state. The term ''reflection'' is sometimes used for a larger class of mappings from a Euclidean space to itself, namely the non-identity isometries that are involutions. Such isometries have a set of fixed points (the "mirror") that is an affine subspace, but is possibly smaller than a hy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotations
Rotation, or spin, is the circular movement of an object around a '' central axis''. A two-dimensional rotating object has only one possible central axis and can rotate in either a clockwise or counterclockwise direction. A three-dimensional object has an infinite number of possible central axes and rotational directions. If the rotation axis passes internally through the body's own center of mass, then the body is said to be ''autorotating'' or '' spinning'', and the surface intersection of the axis can be called a ''pole''. A rotation around a completely external axis, e.g. the planet Earth around the Sun, is called ''revolving'' or ''orbiting'', typically when it is produced by gravity, and the ends of the rotation axis can be called the ''orbital poles''. Mathematics Mathematically, a rotation is a rigid body movement which, unlike a translation, keeps a point fixed. This definition applies to rotations within both two and three dimensions (in a plane and in space, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parity (mathematics)
In mathematics, parity is the property of an integer of whether it is even or odd. An integer is even if it is a multiple of two, and odd if it is not.. For example, −4, 0, 82 are even because \begin -2 \cdot 2 &= -4 \\ 0 \cdot 2 &= 0 \\ 41 \cdot 2 &= 82 \end By contrast, −3, 5, 7, 21 are odd numbers. The above definition of parity applies only to integer numbers, hence it cannot be applied to numbers like 1/2 or 4.201. See the section "Higher mathematics" below for some extensions of the notion of parity to a larger class of "numbers" or in other more general settings. Even and odd numbers have opposite parities, e.g., 22 (even number) and 13 (odd number) have opposite parities. In particular, the parity of zero is even. Any two consecutive integers have opposite parity. A number (i.e., integer) expressed in the decimal numeral system is even or odd according to whether its last digit is even or odd. That is, if the last digit is 1, 3, 5, 7, or 9, then it is odd; otherwis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lo Shu Square
The Luoshu (pinyin), Lo Shu ( Wade-Giles), or Nine Halls Diagram is an ancient Chinese diagram and named for the Luo River near Luoyang, Henan. The Luoshu appears in myths concerning the invention of writing by Cangjie and other culture heroes. It is a unique normal magic square of order three. It is usually paired with the River Map or Hetunamed in reference to the Yellow Riverand used with the River Map in various contexts involving Chinese geomancy, numerology, philosophy, and early natural science. Traditions The Lo Shu is part of the legacy of ancient Chinese mathematical and divinity (cf. the I Ching ) traditions, and is an important emblem in '' Feng Shui'' ()—the art of geomancy concerned with the placement of objects in relation to the flow of qi (), or "natural energy". History A Chinese legend concerning the pre-historic Emperor Yu () tells of the Lo Shu, often in connection with the ''Yellow River Map'' (Hetu) and the eight trigrams. In ancient China there i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic Progression
An arithmetic progression or arithmetic sequence () is a sequence of numbers such that the difference between the consecutive terms is constant. For instance, the sequence 5, 7, 9, 11, 13, 15, . . . is an arithmetic progression with a common difference of 2. If the initial term of an arithmetic progression is a and the common difference of successive members is d, then the n-th term of the sequence (a_n) is given by: :a_n = a + (n - 1)d, If there are ''m'' terms in the AP, then a_m represents the last term which is given by: :a_m = a + (m - 1)d. A finite portion of an arithmetic progression is called a finite arithmetic progression and sometimes just called an arithmetic progression. The sum of a finite arithmetic progression is called an arithmetic series. Sum Computation of the sum 2 + 5 + 8 + 11 + 14. When the sequence is reversed and added to itself term by term, the resulting sequence has a single repeated value in it, equal to the sum of the first and last numbers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
India
India, officially the Republic of India (Hindi: ), is a country in South Asia. It is the seventh-largest country by area, the second-most populous country, and the most populous democracy in the world. Bounded by the Indian Ocean on the south, the Arabian Sea on the southwest, and the Bay of Bengal on the southeast, it shares land borders with Pakistan to the west; China, Nepal, and Bhutan to the north; and Bangladesh and Myanmar to the east. In the Indian Ocean, India is in the vicinity of Sri Lanka and the Maldives; its Andaman and Nicobar Islands share a maritime border with Thailand, Myanmar, and Indonesia. Modern humans arrived on the Indian subcontinent from Africa no later than 55,000 years ago., "Y-Chromosome and Mt-DNA data support the colonization of South Asia by modern humans originating in Africa. ... Coalescence dates for most non-European populations average to between 73–55 ka.", "Modern human beings—''Homo sapiens''—originated in Africa. Then, int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |