|
Supertoroid
In geometry and computer graphics, a supertoroid or supertorus is usually understood to be a family of doughnut-like surfaces (technically, a topological torus) whose shape is defined by mathematical formulas similar to those that define the superellipsoids. The plural of "supertorus" is either supertori or supertoruses. The family was described and named by Alan Barr in 1994.Alan H. Barr (1981) ''Superquadrics and Angle-Preserving Transformations''. IEEE Computer Graphics and Applications, volume 1 issue 1. pp. 11-23. Barr's supertoroids have been fairly popular in computer graphics as a convenient model for many objects, such as smooth frames for rectangular things. One quarter of a supertoroid can provide a smooth and seamless 90-degree joint between two superquadric cylinders. However, they are not algebraic surfaces (except in special cases). Formulas Alan Barr's supertoroids are defined by parametric equations similar to the trigonometric equations of the torus, excep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted as \sin(\theta) and \cos(\theta). The definitions of sine and cosine have been extended to any real number, real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as Series (mathematics), infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic function, periodic pheno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
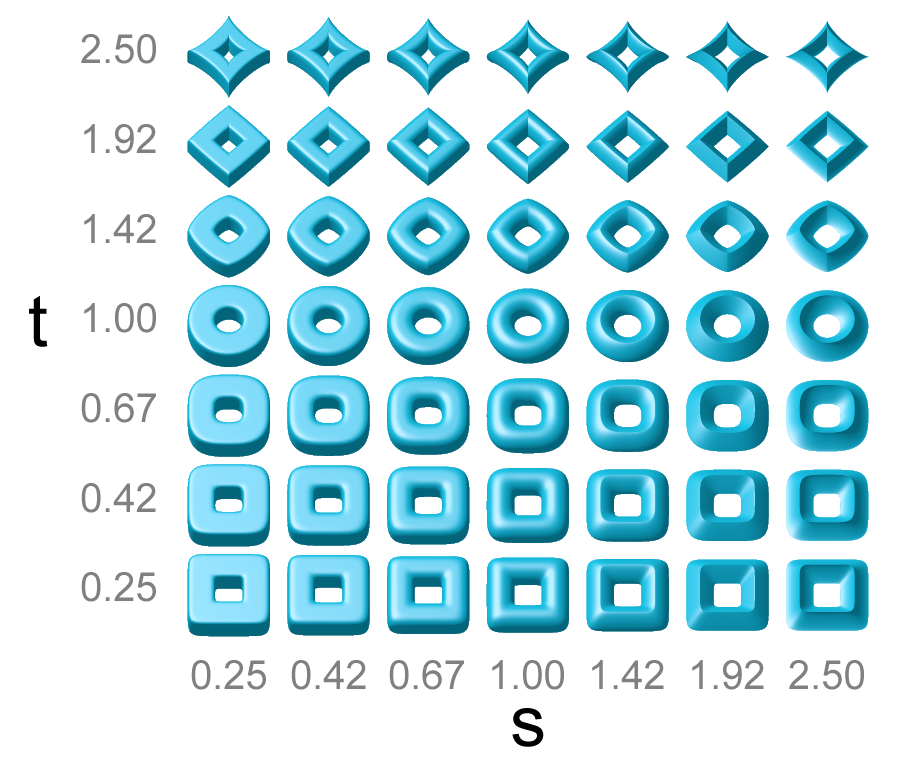
Superquadric
In mathematics, the superquadrics or super-quadrics (also superquadratics) are a family of geometric shapes defined by formulas that resemble those of ellipsoids and other quadrics, except that the squaring operations are replaced by arbitrary powers. They can be seen as the three-dimensional relatives of the superellipses. The term may refer to the solid object or to its surface, depending on the context. The equations below specify the surface; the solid is specified by replacing the equality signs by less-than-or-equal signs. The superquadrics include many shapes that resemble cubes, octahedra, cylinders, lozenges and spindles, with rounded or sharp corners. Because of their flexibility and relative simplicity, they are popular geometric modeling tools, especially in computer graphics. It becomes an important geometric primitive widely used in computer vision, robotics, and physical simulation. Some authors, such as Alan Barr, define "superquadrics" as including both the su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superegg
In geometry, a superegg is a solid of revolution obtained by rotating an elongated superellipse with exponent greater than 2 around its longest axis. It is a special case of superellipsoid. Unlike an elongated ellipsoid, an elongated superegg can stand upright on a flat surface, or on top of another superegg. This is due to its curvature being zero at the tips. The shape was popularized by Danish poet and scientist Piet Hein (1905–1996). Supereggs of various materials, including brass, were sold as novelties or " executive toys" in the 1960s. Mathematical description The superegg is a superellipsoid whose horizontal cross-sections are circles. It is defined by the inequality :\left, \frac\^p + \left, \frac\^p \leq 1 \, , where ''R'' is the horizontal radius at the "equator" (the widest part as defined by the circles), and ''h'' is one half of the height. The exponent ''p'' determines the degree of flattening at the tips and equator. Hein's choice was ''p'' = 2.5 (the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superellipsoid
In mathematics, a superellipsoid (or super-ellipsoid) is a solid geometry, solid whose horizontal sections are superellipses (Lamé curves) with the same squareness parameter \epsilon_2, and whose vertical sections through the center are superellipses with the squareness parameter \epsilon_1. It is a generalization of an ellipsoid, which is a special case when \epsilon_1=\epsilon_2=1. Superellipsoids as computer graphics primitives were popularized by Alan H. Barr (who used the name "superquadrics" to refer to both superellipsoids and supertoroids).Barr, A.H. (1992), ''Rigid Physically Based Superquadrics''. Chapter III.8 of ''Graphics Gems III'', edited by D. Kirk, pp. 137–159 In modern computer vision and robotics literatures, superquadrics and superellipsoids are used interchangeably, since superellipsoids are the most representative and widely utilized shape among all the superquadrics. Superellipsoids have a rich shape vocabulary, including cuboids, cylinders, ellipso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
GNU Octave
GNU Octave is a scientific programming language for scientific computing and numerical computation. Octave helps in solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB. It may also be used as a Batch processing, batch-oriented language. As part of the GNU Project, it is free software under the terms of the GNU General Public License. History The project was conceived around 1988. At first it was intended to be a companion to a chemical reactor design course. Full development was started by John W. Eaton in 1992. The first alpha release dates back to 4 January 1993 and on 17 February 1994 version 1.0 was released. Version 9.2.0 was released on 7 June 2024. The program is named after Octave Levenspiel, a former professor of the principal author. Levenspiel was known for his ability to perform quick back-of-the-envelope calculations. Development history Developments In addition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lamé Curve
A superellipse, also known as a Lamé curve after Gabriel Lamé, is a closed curve resembling the ellipse, retaining the geometric features of semi-major axis and semi-minor axis, and symmetry about them, but defined by an equation that allows for various shapes between a rectangle and an ellipse. In two dimensional Cartesian coordinate system, a superellipse is defined as the set of all points (x,y) on the curve that satisfy the equation\left, \frac\^n\!\! + \left, \frac\^n\! = 1,where a and b are positive numbers referred to as semi-diameters or semi-axes of the superellipse, and n is a positive parameter that defines the shape. When n=2, the superellipse is an ordinary ellipse. For n>2, the shape is more rectangular with rounded corners, and for 0 [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval (mathematics)
In mathematics, a real interval is the set of all real numbers lying between two fixed endpoints with no "gaps". Each endpoint is either a real number or positive or negative infinity, indicating the interval extends without a bound. A real interval can contain neither endpoint, either endpoint, or both endpoints, excluding any endpoint which is infinite. For example, the set of real numbers consisting of , , and all numbers in between is an interval, denoted and called the unit interval; the set of all positive real numbers is an interval, denoted ; the set of all real numbers is an interval, denoted ; and any single real number is an interval, denoted . Intervals are ubiquitous in mathematical analysis. For example, they occur implicitly in the epsilon-delta definition of continuity; the intermediate value theorem asserts that the image of an interval by a continuous function is an interval; integrals of real functions are defined over an interval; etc. Interval ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant under some Transformation (function), transformations, such as Translation (geometry), translation, Reflection (mathematics), reflection, Rotation (mathematics), rotation, or Scaling (geometry), scaling. Although these two meanings of the word can sometimes be told apart, they are intricately related, and hence are discussed together in this article. Mathematical symmetry may be observed with respect to the passage of time; as a space, spatial relationship; through geometric transformations; through other kinds of functional transformations; and as an aspect of abstract objects, including scientific model, theoretic models, language, and music. This article describes symmetry from three perspectives: in mathematics, including geometry, the m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at the centre of a circle by an Circular arc, arc that is equal in length to the radius. The unit was formerly an SI supplementary unit and is currently a dimensionless unit, dimensionless SI derived unit,: "The CGPM decided to interpret the supplementary units in the SI, namely the radian and the steradian, as dimensionless derived units." defined in the SI as 1 rad = 1 and expressed in terms of the SI base unit metre (m) as . Angles without explicitly specified units are generally assumed to be measured in radians, especially in mathematical writing. Definition One radian is defined as the angle at the center of a circle in a plane that wikt:subtend, subtends an arc whose length equals the radius of the circle. More generally, the magnit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sign Function
In mathematics, the sign function or signum function (from '' signum'', Latin for "sign") is a function that has the value , or according to whether the sign of a given real number is positive or negative, or the given number is itself zero. In mathematical notation the sign function is often represented as \sgn x or \sgn (x). Definition The signum function of a real number x is a piecewise function which is defined as follows: \sgn x :=\begin -1 & \text x 0. \end The law of trichotomy states that every real number must be positive, negative or zero. The signum function denotes which unique category a number falls into by mapping it to one of the values , or which can then be used in mathematical expressions or further calculations. For example: \begin \sgn(2) &=& +1\,, \\ \sgn(\pi) &=& +1\,, \\ \sgn(-8) &=& -1\,, \\ \sgn(-\frac) &=& -1\,, \\ \sgn(0) &=& 0\,. \end Basic properties Any real number can be expressed as the product of its absolute value and its sig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, is the product (mathematics), product of multiplying bases: b^n = \underbrace_.In particular, b^1=b. The exponent is usually shown as a superscript to the right of the base as or in computer code as b^n. This binary operation is often read as " to the power "; it may also be referred to as " raised to the th power", "the th power of ", or, most briefly, " to the ". The above definition of b^n immediately implies several properties, in particular the multiplication rule:There are three common notations for multiplication: x\times y is most commonly used for explicit numbers and at a very elementary level; xy is most common when variable (mathematics), variables are used; x\cdot y is used for emphasizing that one ta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |