|
Strongly Correlated Material
Strongly correlated materials are a wide class of compounds that include insulators and electronic materials, and show unusual (often technologically useful) electronic and magnetic properties, such as metal-insulator transitions, heavy fermion behavior, half-metallicity, and spin-charge separation. The essential feature that defines these materials is that the behavior of their electrons or spinons cannot be described effectively in terms of non-interacting entities. Theoretical models of the electronic ( fermionic) structure of strongly correlated materials must include electronic ( fermionic) correlation to be accurate. As of recently, the label quantum materials is also used to refer to strongly correlated materials, among others. Transition metal oxides Many transition metal oxides belong to this class which may be subdivided according to their behavior, ''e.g.'' high-Tc, spintronic materials, multiferroics, Mott insulators, spin Peierls materials, heavy ferm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
High-temperature Superconductivity
High-temperature superconductivity (high-c or HTS) is superconductivity in materials with a critical temperature (the temperature below which the material behaves as a superconductor) above , the boiling point of liquid nitrogen. They are "high-temperature" only relative to previously known superconductors, which function only closer to absolute zero. The first high-temperature superconductor was discovered in 1986 by IBM researchers Georg Bednorz and K. Alex Müller. Although the critical temperature is around , this material was modified by Ching-Wu Chu to make the first high-temperature superconductor with critical temperature . Bednorz and Müller were awarded the Nobel Prize in Physics in 1987 "for their important break-through in the discovery of superconductivity in ceramic materials". Most high-c materials are type-II superconductors. The major advantage of high-temperature superconductors is that they can be cooled using liquid nitrogen, in contrast to previously known s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
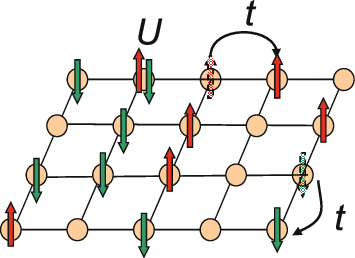
Hubbard Model
The Hubbard model is an Approximation, approximate model used to describe the transition between Conductor (material), conducting and Electrical insulation, insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard (physicist), John Hubbard. The Hubbard model states that each electron experiences competing forces: one pushes it to tunnel to neighboring atoms, while the other pushes it away from its neighbors. Its Hamiltonian (quantum mechanics), Hamiltonian thus has two terms: a kinetic term allowing for Quantum tunneling, tunneling ("hopping") of particles between lattice sites and a potential term reflecting on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, in which case the model is referred to as the "Bose–Hubbard model". The Hubbard model is a useful approximation for particles in a periodic potential at sufficiently low temperatures, where all the particles may be assumed t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian (quantum Mechanics)
In quantum mechanics, the Hamiltonian of a system is an operator corresponding to the total energy of that system, including both kinetic energy and potential energy. Its spectrum, the system's ''energy spectrum'' or its set of ''energy eigenvalues'', is the set of possible outcomes obtainable from a measurement of the system's total energy. Due to its close relation to the energy spectrum and time-evolution of a system, it is of fundamental importance in most formulations of quantum theory. The Hamiltonian is named after William Rowan Hamilton, who developed a revolutionary reformulation of Newtonian mechanics, known as Hamiltonian mechanics, which was historically important to the development of quantum physics. Similar to vector notation, it is typically denoted by \hat, where the hat indicates that it is an operator. It can also be written as H or \check. Introduction The Hamiltonian of a system represents the total energy of the system; that is, the sum of the kine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
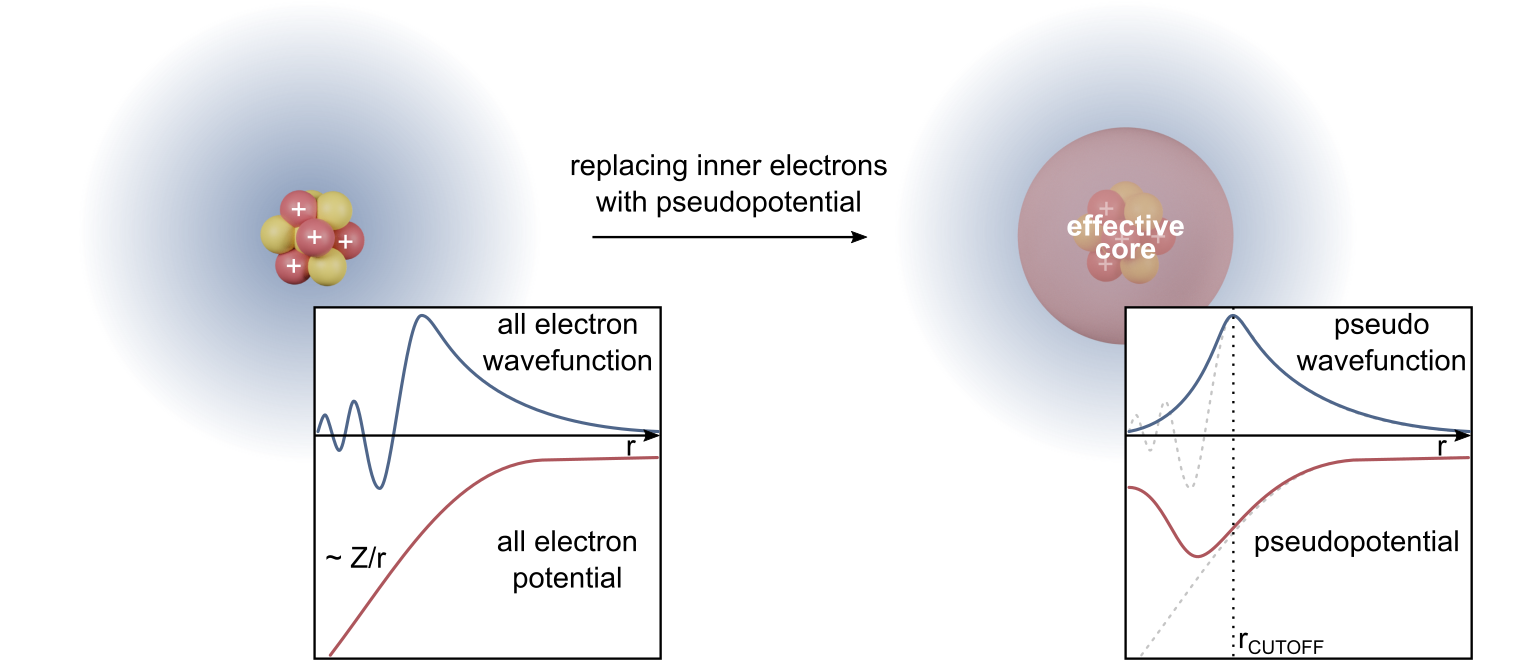
GW Approximation
The ''GW'' approximation (GWA) is an approximation made in order to calculate the self-energy of a many-body system of electrons. The approximation is that the expansion of the self-energy ''Σ'' in terms of the single particle Green's function ''G'' and the screened Coulomb interaction ''W'' (in units of \hbar=1) : \Sigma = iGW - GWGWG + \cdots can be truncated after the first term: : \Sigma \approx iG W In other words, the self-energy is expanded in a formal Taylor series in powers of the screened interaction ''W'' and the lowest order term is kept in the expansion in GWA. Theory The above formulae are schematic in nature and show the overall idea of the approximation. More precisely, if we label an electron coordinate with its position, spin, and time and bundle all three into a composite index (the numbers 1, 2, etc.), we have : \Sigma(1,2) = iG(1,2)W(1^+,2) - \int d3 \int d4 \, G(1,3)G(3,4)G(4,2)W(1,4)W(3,2) + ... where the "+" superscript means the time index is shi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Band Gap
In solid-state physics and solid-state chemistry, a band gap, also called a bandgap or energy gap, is an energy range in a solid where no electronic states exist. In graphs of the electronic band structure of solids, the band gap refers to the energy difference (often expressed in electronvolts) between the top of the valence band and the bottom of the conduction band in insulators and semiconductors. It is the energy required to promote an electron from the valence band to the conduction band. The resulting conduction-band electron (and the electron hole in the valence band) are free to move within the crystal lattice and serve as charge carriers to conduct electric current. It is closely related to the HOMO/LUMO gap in chemistry. If the valence band is completely full and the conduction band is completely empty, then electrons cannot move within the solid because there are no available states. If the electrons are not free to move within the crystal lattice, then there ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coulomb Repulsion
Coulomb's inverse-square law, or simply Coulomb's law, is an experimental law of physics that calculates the amount of force between two electrically charged particles at rest. This electric force is conventionally called the ''electrostatic force'' or Coulomb force. Although the law was known earlier, it was first published in 1785 by French physicist Charles-Augustin de Coulomb. Coulomb's law was essential to the development of the theory of electromagnetism and maybe even its starting point, as it allowed meaningful discussions of the amount of electric charge in a particle. The law states that the magnitude, or absolute value, of the attractive or repulsive electrostatic force between two point charges is directly proportional to the product of the magnitudes of their charges and inversely proportional to the square of the distance between them. Coulomb discovered that bodies with like electrical charges repel: Coulomb also showed that oppositely charged bodies attract ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
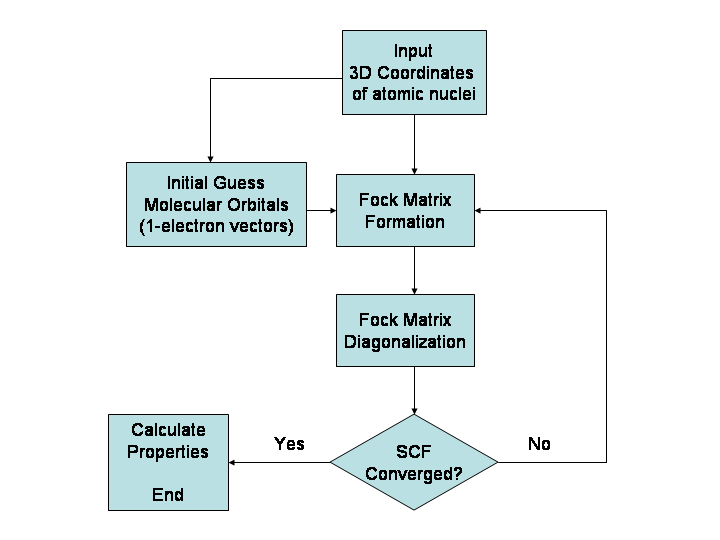
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The method is named after Douglas Hartree and Vladimir Fock. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Hartree–Fock approximation is an instance of mean-field theory, where neglecting higher-order fluctuations in order parameter allows interaction terms to be replaced with quadratic terms, obtaining exactly solvable Hamiltonians. Especially ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density-functional Theory
Density functional theory (DFT) is a computational quantum mechanics, quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure (or nuclear structure) (principally the ground state) of Many-body problem, many-body systems, in particular atoms, molecules, and the condensed phases. Using this theory, the properties of a many-electron system can be determined by using Functional (mathematics), functionals - that is, functions that accept a function as input and output a single real number. In the case of DFT, these are functionals of the spatially dependent electronic density, electron density. DFT is among the most popular and versatile methods available in condensed-matter physics, computational physics, and computational chemistry. DFT has been very popular for calculations in solid-state physics since the 1970s. However, DFT was not considered accurate enough for calculations in quantum chemistry until the 1990 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local-density Approximation
Local-density approximations (LDA) are a class of approximations to the exchange–correlation (XC) energy functional in density functional theory (DFT) that depend solely upon the value of the electronic density at each point in space (and not, for example, derivatives of the density or the Kohn–Sham orbitals). Many approaches can yield local approximations to the XC energy. However, overwhelmingly successful local approximations are those that have been derived from the homogeneous electron gas (HEG) model. In this regard, LDA is generally synonymous with functionals based on the HEG approximation, which are then applied to realistic systems (molecules and solids). In general, for a spin-unpolarized system, a local-density approximation for the exchange-correlation energy is written as :E_^rho= \int \rho(\mathbf)\epsilon_(\rho(\mathbf))\ \mathrm\mathbf\ , where ''ρ'' is the electronic density and ''єxc'' is the exchange-correlation energy per particle of a homogen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Field Theory
In physics and probability theory, Mean-field theory (MFT) or Self-consistent field theory studies the behavior of high-dimensional random (stochastic) models by studying a simpler model that approximates the original by averaging over degrees of freedom (the number of values in the final calculation of a statistic that are free to vary). Such models consider many individual components that interact with each other. The main idea of MFT is to replace all interactions to any one body with an average or effective interaction, sometimes called a ''molecular field''. This reduces any many-body problem into an effective one-body problem. The ease of solving MFT problems means that some insight into the behavior of the system can be obtained at a lower computational cost. MFT has since been applied to a wide range of fields outside of physics, including statistical inference, graphical models, neuroscience, artificial intelligence, epidemic models, queueing theory, computer-network ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi Sea
The Fermi energy is a concept in quantum mechanics usually referring to the energy difference between the highest and lowest occupied single-particle states in a quantum system of non-interacting fermions at absolute zero temperature. In a Fermi gas, the lowest occupied state is taken to have zero kinetic energy, whereas in a metal, the lowest occupied state is typically taken to mean the bottom of the conduction band. The term "Fermi energy" is often used to refer to a different yet closely related concept, the Fermi ''level'' (also called electrochemical potential).The use of the term "Fermi energy" as synonymous with Fermi level (a.k.a. electrochemical potential) is widespread in semiconductor physics. For example:''Electronics (fundamentals And Applications)''by D. Chattopadhyay''Semiconductor Physics and Applications''by Balkanski and Wallis. There are a few key differences between the Fermi level and Fermi energy, at least as they are used in this article: * The Fermi energ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |