|
Strain Rate
In mechanics and materials science, strain rate is the time derivative of strain of a material. Strain rate has dimension of inverse time and SI units of inverse second, s−1 (or its multiples). The strain rate at some point within the material measures the rate at which the distances of adjacent parcels of the material change with time in the neighborhood of that point. It comprises both the rate at which the material is expanding or shrinking (expansion rate), and also the rate at which it is being deformed by progressive shearing without changing its volume ( shear rate). It is zero if these distances do not change, as happens when all particles in some region are moving with the same velocity (same speed and direction) and/or rotating with the same angular velocity, as if that part of the medium were a rigid body. The strain rate is a concept of materials science and continuum mechanics that plays an essential role in the physics of fluids and deformable solids. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanics
Mechanics () is the area of physics concerned with the relationships between force, matter, and motion among Physical object, physical objects. Forces applied to objects may result in Displacement (vector), displacements, which are changes of an object's position relative to its environment. Theoretical expositions of this branch of physics has its origins in Ancient Greece, for instance, in the writings of Aristotle and Archimedes (see History of classical mechanics and Timeline of classical mechanics). During the early modern period, scientists such as Galileo Galilei, Johannes Kepler, Christiaan Huygens, and Isaac Newton laid the foundation for what is now known as classical mechanics. As a branch of classical physics, mechanics deals with bodies that are either at rest or are moving with velocities significantly less than the speed of light. It can also be defined as the physical science that deals with the motion of and forces on bodies not in the quantum realm. History ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newtonian Fluid
A Newtonian fluid is a fluid in which the viscous stresses arising from its flow are at every point linearly correlated to the local strain rate — the rate of change of its deformation over time. Stresses are proportional to the rate of change of the fluid's velocity vector. A fluid is Newtonian only if the tensors that describe the viscous stress and the strain rate are related by a constant viscosity tensor that does not depend on the stress state and velocity of the flow. If the fluid is also isotropic (i.e., its mechanical properties are the same along any direction), the viscosity tensor reduces to two real coefficients, describing the fluid's resistance to continuous shear deformation and continuous compression or expansion, respectively. Newtonian fluids are the easiest mathematical models of fluids that account for viscosity. While no real fluid fits the definition perfectly, many common liquids and gases, such as water and air, can be assumed to be Newtonian fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pipe (fluid Conveyance)
Pipe(s), PIPE(S) or piping may refer to: Objects * Pipe (fluid conveyance), a hollow cylinder following certain dimension rules ** Piping, the use of pipes in industry * Smoking pipe ** Tobacco pipe * Half-pipe and quarter pipe, semi-circular ramps for performing skateboarding/snowboarding tricks * Piping (sewing), tubular ornamental fabric sewn around the edge of a garment * ''For the musical instruments'', see #Music, below Music * Pipe (instrument), a traditional perforated wind instrument * Bagpipe, a class of musical instrument, aerophones using enclosed reeds ** Pipes and drums or pipe bands, composed of musicians who play the Scottish and Irish bagpipes * Organ pipe, one of the tuned resonators that produces the main sound of a pipe organ * Pan pipes, see Pan flute, an ancient musical instrument based on the principle of the stopped pipe * Piped music, or elevator music, a type of background music * "Pipe", by Christie Front Drive from ''Christie Front Drive (EP), Christ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
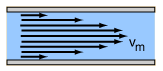
Couette Flow
In fluid dynamics, Couette flow is the flow of a viscosity, viscous fluid in the space between two surfaces, one of which is moving tangentially relative to the other. The relative motion of the surfaces imposes a shear stress on the fluid and induces flow. Depending on the definition of the term, there may also be an applied pressure gradient in the flow direction. The Couette configuration models certain practical problems, like the Earth's mantle and Atmosphere of Earth, atmosphere, and flow in lightly loaded Fluid bearing, journal bearings. It is also employed in Viscometer, viscometry and to demonstrate approximations of Time reversibility, reversibility. It is named after Maurice Couette, a Professor of Physics at the French University of Angers in the late 19th century. Isaac Newton first defined the problem of Couette flow in Proposition 51 of his Philosophiæ Naturalis Principia Mathematica, ''Philosophiæ Naturalis Principia Mathematica'', and expanded upon the ideas i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laminar Flow
Laminar flow () is the property of fluid particles in fluid dynamics to follow smooth paths in layers, with each layer moving smoothly past the adjacent layers with little or no mixing. At low velocities, the fluid tends to flow without lateral mixing, and adjacent layers slide past one another smoothly. There are no cross-currents perpendicular to the direction of flow, nor eddies or swirls of fluids. In laminar flow, the motion of the particles of the fluid is very orderly with particles close to a solid surface moving in straight lines parallel to that surface. Laminar flow is a flow regime characterized by high momentum diffusion and low momentum convection. When a fluid is flowing through a closed channel such as a pipe or between two flat plates, either of two types of flow may occur depending on the velocity and viscosity of the fluid: laminar flow or turbulent flow. Laminar flow occurs at lower velocities, below a threshold at which the flow becomes turbulent. The thresh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinitesimal
In mathematics, an infinitesimal number is a non-zero quantity that is closer to 0 than any non-zero real number is. The word ''infinitesimal'' comes from a 17th-century Modern Latin coinage ''infinitesimus'', which originally referred to the "infinity- th" item in a sequence. Infinitesimals do not exist in the standard real number system, but they do exist in other number systems, such as the surreal number system and the hyperreal number system, which can be thought of as the real numbers augmented with both infinitesimal and infinite quantities; the augmentations are the reciprocals of one another. Infinitesimal numbers were introduced in the development of calculus, in which the derivative was first conceived as a ratio of two infinitesimal quantities. This definition was not rigorously formalized. As calculus developed further, infinitesimals were replaced by limits, which can be calculated using the standard real numbers. In the 3rd century BC Archimedes used what ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measurement Unit
A unit of measurement, or unit of measure, is a definite magnitude (mathematics), magnitude of a quantity, defined and adopted by convention or by law, that is used as a standard for measurement of the same kind of quantity. Any other quantity of that kind can be expressed as a multiple of the unit of measurement. For example, a length is a physical quantity. The metre (symbol m) is a unit of length that represents a definite predetermined length. For instance, when referencing "10 metres" (or 10 m), what is actually meant is 10 times the definite predetermined length called "metre". The definition, agreement, and practical use of units of measurement have played a crucial role in human endeavour from early ages up to the present. A multitude of System of measurement, systems of units used to be very common. Now there is a global standard, the International System of Units (SI), the modern form of the metric system. In trade, weights and measures are often a su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionless
Dimensionless quantities, or quantities of dimension one, are quantities implicitly defined in a manner that prevents their aggregation into units of measurement. ISBN 978-92-822-2272-0. Typically expressed as ratios that align with another system, these quantities do not necessitate explicitly defined units. For instance, alcohol by volume (ABV) represents a volumetric ratio; its value remains independent of the specific units of volume used, such as in milliliters per milliliter (mL/mL). The number one is recognized as a dimensionless base quantity. Radians serve as dimensionless units for angular measurements, derived from the universal ratio of 2π times the radius of a circle being equal to its circumference. Dimensionless quantities play a crucial role serving as parameters in differential equations in various technical disciplines. In calculus, concepts like the unitless ratios in limits or derivatives often involve dimensionless quantities. In differential geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation. There are multiple different notations for differentiation. '' Leibniz notation'', named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas ''prime notation'' is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brittle
A material is brittle if, when subjected to stress, it fractures with little elastic deformation and without significant plastic deformation. Brittle materials absorb relatively little energy prior to fracture, even those of high strength. Breaking is often accompanied by a sharp snapping sound. When used in materials science, it is generally applied to materials that fail when there is little or no plastic deformation before failure. One proof is to match the broken halves, which should fit exactly since no plastic deformation has occurred. Brittleness in different materials Polymers Mechanical characteristics of polymers can be sensitive to temperature changes near room temperatures. For example, poly(methyl methacrylate) is extremely brittle at temperature 4˚C, but experiences increased ductility with increased temperature. Amorphous polymers are polymers that can behave differently at different temperatures. They may behave like a glass at low temperatures (the gla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ductile
Ductility refers to the ability of a material to sustain significant plastic deformation before fracture. Plastic deformation is the permanent distortion of a material under applied stress, as opposed to elastic deformation, which is reversible upon removing the stress. Ductility is a critical mechanical performance indicator, particularly in applications that require materials to bend, stretch, or deform in other ways without breaking. The extent of ductility can be quantitatively assessed using the percent elongation at break, given by the equation: \% \mathrm= \left ( \frac \right )\times100 where l_ is the length of the material after fracture and l_0 is the original length before testing. This formula helps in quantifying how much a material can stretch under tensile stress before failure, providing key insights into its ductile behavior. Ductility is an important consideration in engineering and manufacturing. It defines a material's suitability for certain manufactur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |