|
Stochastic Game
In game theory, a stochastic game (or Markov game) is a repeated game with probabilistic transitions played by one or more players. The game is played in a sequence of stages. At the beginning of each stage the game is in some state. The players select actions and each player receives a payoff that depends on the current state and the chosen actions. The game then moves to a new random state whose distribution depends on the previous state and the actions chosen by the players. The procedure is repeated at the new state and play continues for a finite or infinite number of stages. The total payoff to a player is often taken to be the discounted sum of the stage payoffs or the limit inferior of the averages of the stage payoffs. Stochastic games were introduced by Lloyd Shapley in the early 1950s. They generalize Markov decision processes to multiple interacting decision makers, as well as strategic-form games to dynamic situations in which the environment changes in response to t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed two-person zero-sum games, in which a participant's gains or losses are exactly balanced by the losses and gains of the other participant. In the 1950s, it was extended to the study of non zero-sum games, and was eventually applied to a wide range of Human behavior, behavioral relations. It is now an umbrella term for the science of rational Decision-making, decision making in humans, animals, and computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum games and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathematical economics. His paper was f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jerzy Andrzej Filar
Jerzy Andrzej Filar (born August 30, 1949, in Warsaw, Żoliborz) is an Australian mathematician of Polish origin, known for his contributions to operations research, stochastic modelling, game theory, Markov decision processes, perturbation theory, and environmental modelling. Biography He received his early education at Primary School No. 1 in Warsaw. In 1964, he moved to Melbourne, Australia, where he attended Kew High School. In 1972, he obtained a B.Sc (Hons) degree in Mathematical Statistics from the University of Melbourne, followed by an M.Sc. in Statistics from Monash University in 1975, and a M.A. in Mathematics from University of Illinois Chicago in 1977.The documents concerning education are in the private archive of Filar's family In 1980, he completed his PhD at the University of Illinois Chicago, defending his thesis titled ''Algorithms for Solving Undiscounted Stochastic Games''. His doctoral advisor was T.E.S. Raghavan. Academic career Since 1975, Jerzy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Process
In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables in a probability space, where the index of the family often has the interpretation of time. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology Ecology () is the natural science of the relationships among living organisms and their Natural environment, environment. Ecology considers organisms at the individual, population, community (ecology), community, ecosystem, and biosphere lev ..., neuroscience, physics, image processing, signal processing, stochastic control, control theory, information theory, computer scien ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evolutionary Biology
Evolutionary biology is the subfield of biology that studies the evolutionary processes such as natural selection, common descent, and speciation that produced the diversity of life on Earth. In the 1930s, the discipline of evolutionary biology emerged through what Julian Huxley called the Modern synthesis (20th century), modern synthesis of understanding, from previously unrelated fields of biological research, such as genetics and ecology, systematics, and paleontology. The investigational range of current research has widened to encompass the genetic architecture of adaptation, molecular evolution, and the different forces that contribute to evolution, such as sexual selection, genetic drift, and biogeography. The newer field of evolutionary developmental biology ("evo-devo") investigates how embryogenesis is controlled, thus yielding a wider synthesis that integrates developmental biology with the fields of study covered by the earlier evolutionary synthesis. Subfields ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services. Economics focuses on the behaviour and interactions of Agent (economics), economic agents and how economy, economies work. Microeconomics analyses what is viewed as basic elements within economy, economies, including individual agents and market (economics), markets, their interactions, and the outcomes of interactions. Individual agents may include, for example, households, firms, buyers, and sellers. Macroeconomics analyses economies as systems where production, distribution, consumption, savings, and Expenditure, investment expenditure interact; and the factors of production affecting them, such as: Labour (human activity), labour, Capital (economics), capital, Land (economics), land, and Entrepreneurship, enterprise, inflation, economic growth, and public policies that impact gloss ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eugene Dynkin
Eugene Borisovich Dynkin (; 11 May 1924 – 14 November 2014) was a Soviet and American mathematician. He made contributions to the fields of probability and algebra, especially semisimple Lie groups, Lie algebras, and Markov processes. The Dynkin diagram, the Dynkin system, and Dynkin's lemma are named after him. Biography Dynkin was born into a Jewish family, living in Leningrad until 1935, when his family was exiled to Kazakhstan. Two years later, when Dynkin was 13, his father disappeared in the Gulag. Moscow University At the age of 16, in 1940, Dynkin was admitted to Moscow University. He avoided military service in World War II because of his poor eyesight, and received his MS in 1945 and his PhD in 1948. He became an assistant professor at Moscow, but was not awarded a "chair" until 1954 because of his political undesirability. His academic progress was made difficult due to his father's fate, as well as Dynkin's Jewish origin; the special efforts of Andrey Kolmogoro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
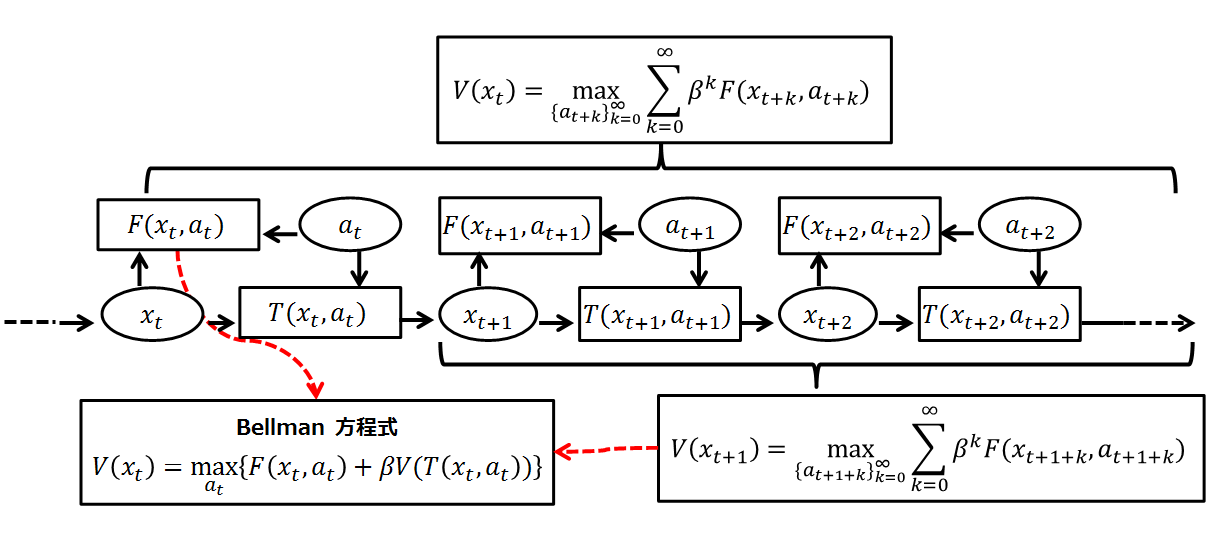
Bellman Equation
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical Optimization (mathematics), optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used. The Bellman equation was first applied to engineering control theory and to other topics in applied mathematics, and subsequently became an important tool in economic theory; though the basic concepts of dynamic programming are prefigured in John von Neumann and Oskar Morgenstern's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Artificial Intelligence (journal)
''Artificial Intelligence'' is a scientific journal on artificial intelligence research. It was established in 1970 and is published by Elsevier. The journal is abstracted and indexed in Scopus and Science Citation Index. The 2021 Impact Factor for this journal is 14.05 and the 5-Year Impact Factor is 11.616.Journal Citation Reports 2022, Published by Thomson Reuters References External links Official website Artificial intelligence journals Elsevier academic journals Academic journals established in 1970 {{compu-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Game
In game theory, a Bayesian game is a strategic decision-making model which assumes players have incomplete information. Players may hold private information relevant to the game, meaning that the payoffs are not common knowledge. Bayesian games model the outcome of player interactions using aspects of Bayesian probability. They are notable because they allowed the specification of the solutions to games with incomplete information for the first time in game theory. Hungarian economist John C. Harsanyi introduced the concept of Bayesian games in three papers from 1967 and 1968: He was awarded the Nobel Memorial Prize in Economic Sciences for these and other contributions to game theory in 1994. Roughly speaking, Harsanyi defined Bayesian games in the following way: players are assigned a set of characteristics by nature at the start of the game. By mapping probability distributions to these characteristics and by calculating the outcome of the game using Bayesian probability, the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sub-game Perfect Nash Equilibrium
In game theory, a subgame perfect equilibrium (SPE), or subgame perfect Nash equilibrium (SPNE), is a refinement of the Nash equilibrium concept, specifically designed for dynamic games where players make sequential decisions. A strategy profile is an SPE if it represents a Nash equilibrium in every possible subgame of the original game. Informally, this means that at any point in the game, the players' behavior from that point onward should represent a Nash equilibrium of the continuation game (i.e. of the subgame), no matter what happened before. This ensures that strategies are credible and rational throughout the entire game, eliminating non-credible threats. Every finite extensive game with complete information (all players know the complete state of the game) and perfect recall (each player remembers all their previous actions and knowledge throughout the game) has a subgame perfect equilibrium. A common method for finding SPE in finite games is backward induction, wher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Perfect Equilibrium
A Markov perfect equilibrium is an equilibrium concept in game theory. It has been used in analyses of industrial organization, macroeconomics, and political economy. It is a refinement of the concept of subgame perfect equilibrium to extensive form games for which a pay-off relevant state space can be identified. The term appeared in publications starting about 1988 in the work of economists Jean Tirole and Eric Maskin. Definition In extensive form games, and specifically in stochastic games, a Markov perfect equilibrium is a set of mixed strategies for each of the players which satisfy the following criteria: * The strategies have the Markov property of memorylessness, meaning that each player's mixed strategy can be conditioned only on the ''state'' of the game. These strategies are called ''Markov reaction functions''. * The ''state'' can only encode payoff-relevant information. This rules out strategies that depend on non-substantive moves by the opponent. It excludes str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |