|
Steradian
The steradian (symbol: sr) or square radian is the unit of solid angle in the International System of Units (SI). It is used in three-dimensional geometry, and is analogous to the radian, which quantifies planar angles. A solid angle in the form of a circular cone can be projected onto a sphere from its centre, delineating a spherical cap where the cone intersects the sphere. The magnitude of the solid angle expressed in steradians is defined as the quotient of the surface area of the spherical cap and the square of the sphere's radius. This is analogous to the way a plane angle projected onto a circle delineates a circular arc on the circumference, whose length is proportional to the angle. Steradians can be used to measure a solid angle of any projected shape. The solid angle subtended is the same as that of a cone with the same projected area. A solid angle of one steradian subtends a cone aperture of approximately 1.144 radians or 65.54 degrees. In the SI, solid angle i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steradian Cone And Cap
The steradian (symbol: sr) or square radian is the unit of solid angle in the International System of Units (SI). It is used in three-dimensional geometry, and is analogous to the radian, which quantifies planar angles. A solid angle in the form of a circular cone can be projected onto a sphere from its centre, delineating a spherical cap where the cone intersects the sphere. The magnitude of the solid angle expressed in steradians is defined as the quotient of the surface area of the spherical cap and the square of the sphere's radius. This is analogous to the way a plane angle projected onto a circle delineates a circular arc on the circumference, whose length is proportional to the angle. Steradians can be used to measure a solid angle of any projected shape. The solid angle subtended is the same as that of a cone with the same projected area. A solid angle of one steradian subtends a cone aperture of approximately 1.144 radians or 65.54 degrees. In the SI, solid angle is consi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
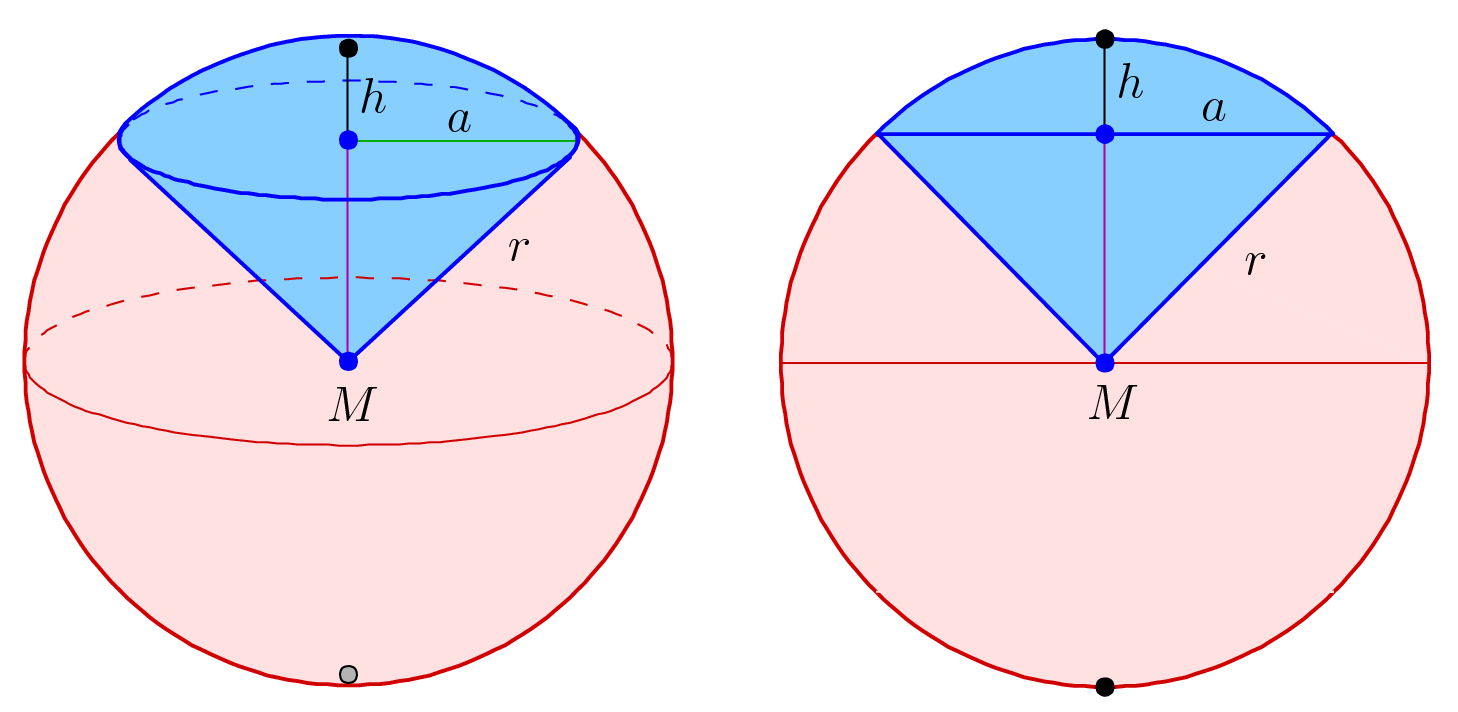
Solid Angle
In geometry, a solid angle (symbol: ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the ''apex'' of the solid angle, and the object is said to '' subtend'' its solid angle at that point. In the International System of Units (SI), a solid angle is expressed in a dimensionless unit called a ''steradian'' (symbol: sr), which is equal to one square radian, sr = rad2. One steradian corresponds to one unit of area (of any shape) on the unit sphere surrounding the apex, so an object that blocks all rays from the apex would cover a number of steradians equal to the total surface area of the unit sphere, 4\pi. Solid angles can also be measured in squares of angular measures such as degrees, minutes, and seconds. A small object nearby may subtend the same solid angle as a larger object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
International System Of Units
The International System of Units, internationally known by the abbreviation SI (from French ), is the modern form of the metric system and the world's most widely used system of measurement. It is the only system of measurement with official status in nearly every country in the world, employed in science, technology, industry, and everyday commerce. The SI system is coordinated by the International Bureau of Weights and Measures, which is abbreviated BIPM from . The SI comprises a coherent system of units of measurement starting with seven base units, which are the second (symbol s, the unit of time), metre (m, length), kilogram (kg, mass), ampere (A, electric current), kelvin (K, thermodynamic temperature), mole (mol, amount of substance), and candela (cd, luminous intensity). The system can accommodate coherent units for an unlimited number of additional quantities. These are called coherent derived units, which can always be represented as products of powers of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SI Derived Unit
SI derived units are units of measurement derived from the seven SI base units specified by the International System of Units (SI). They can be expressed as a product (or ratio) of one or more of the base units, possibly scaled by an appropriate power of exponentiation (see: Buckingham π theorem). Some are dimensionless, as when the units cancel out in ratios of like quantities. SI coherent derived units involve only a trivial proportionality factor, not requiring conversion factors. The SI has special names for 22 of these coherent derived units (for example, hertz, the SI unit of measurement of frequency), but the rest merely reflect their derivation: for example, the square metre (m2), the SI derived unit of area; and the kilogram per cubic metre (kg/m3 or kg⋅m−3), the SI derived unit of density. The names of SI coherent derived units, when written in full, are always in lowercase. However, the symbols for units named after persons are written with an uppercase ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at the centre of a circle by an Circular arc, arc that is equal in length to the radius. The unit was formerly an SI supplementary unit and is currently a dimensionless unit, dimensionless SI derived unit,: "The CGPM decided to interpret the supplementary units in the SI, namely the radian and the steradian, as dimensionless derived units." defined in the SI as 1 rad = 1 and expressed in terms of the SI base unit metre (m) as . Angles without explicitly specified units are generally assumed to be measured in radians, especially in mathematical writing. Definition One radian is defined as the angle at the center of a circle in a plane that wikt:subtend, subtends an arc whose length equals the radius of the circle. More generally, the magnit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radiant Intensity
In radiometry, radiant intensity is the radiant flux emitted, reflected, transmitted or received, per unit solid angle, and spectral intensity is the radiant intensity per unit frequency or wavelength, depending on whether the spectrum is taken as a function of frequency or of wavelength. These are ''directional'' quantities. The SI unit of radiant intensity is the watt per steradian (), while that of spectral intensity in frequency is the watt per steradian per hertz () and that of spectral intensity in wavelength is the watt per steradian per metre ()—commonly the watt per steradian per nanometre (). Radiant intensity is distinct from irradiance and radiant exitance, which are often called ''intensity'' in branches of physics other than radiometry. In radio-frequency engineering, radiant intensity is sometimes called radiation intensity. Mathematical definitions Radiant intensity Radiant intensity, denoted ''I''e,Ω ("e" for "energetic", to avoid confusion with photometric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Sector
In geometry, a spherical sector, also known as a spherical cone, is a portion of a sphere or of a ball defined by a conical boundary with apex at the center of the sphere. It can be described as the union of a spherical cap and the cone formed by the center of the sphere and the base of the cap. It is the three-dimensional analogue of the sector of a circle. Volume If the radius of the sphere is denoted by and the height of the cap by , the volume of the spherical sector is V = \frac\,. This may also be written as V = \frac (1-\cos\varphi)\,, where is half the cone aperture angle, i.e., is the angle between the rim of the cap and the axis direction to the middle of the cap as seen from the sphere center. The limiting case is for approaching 180 degrees, which then describes a complete sphere. The height, is given by h = r (1-\cos\varphi)\,. The volume of the sector is related to the area of the cap by: V = \frac\,. Area The curved surface area of the spherical se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Sphere
In mathematics, a unit sphere is a sphere of unit radius: the locus (mathematics), set of points at Euclidean distance 1 from some center (geometry), center point in three-dimensional space. More generally, the ''unit -sphere'' is an n-sphere, -sphere of unit radius in -dimensional Euclidean space; the unit circle is a special case, the unit -sphere in the Euclidean plane, plane. An (Open set, open) unit ball is the region inside of a unit sphere, the set of points of distance less than 1 from the center. A sphere or ball with unit radius and center at the origin (mathematics), origin of the space is called ''the'' unit sphere or ''the'' unit ball. Any arbitrary sphere can be transformed to the unit sphere by a combination of translation (geometry), translation and scaling (geometry), scaling, so the study of spheres in general can often be reduced to the study of the unit sphere. The unit sphere is often used as a model for spherical geometry because it has constant sectional cu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kind Of Quantity
A physical quantity (or simply quantity) is a property of a material or system that can be quantified by measurement. A physical quantity can be expressed as a ''value'', which is the algebraic multiplication of a '' numerical value'' and a ''unit of measurement''. For example, the physical quantity mass, symbol ''m'', can be quantified as ''m'n''kg, where ''n'' is the numerical value and kg is the unit symbol (for kilogram). Quantities that are vectors have, besides numerical value and unit, direction or orientation in space. Components Following ISO 80000-1, any value or magnitude of a physical quantity is expressed as a comparison to a unit of that quantity. The ''value'' of a physical quantity ''Z'' is expressed as the product of a ''numerical value'' (a pure number) and a unit 'Z'' :Z = \ \times /math> For example, let Z be "2 metres"; then, \ = 2 is the numerical value and = \mathrm is the unit. Conversely, the numerical value expressed in an arbitrary unit can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spat (angular Unit)
The spat (symbol sp), from the Latin ''spatium'' ("space"), is a unit of solid angle. 1 spat is equal to 4 steradians or approximately square degrees of solid angle . Thus it is the solid angle subtended by a complete sphere at its center. The whole sphere contains ~148.510 million square arcminutes and ~534.638 billion square arcseconds. See also * Turn (angle) — the plane angle counterpart of the spat, equivalent to 2 radian The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...s References Units of solid angle {{geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionless Quantity
Dimensionless quantities, or quantities of dimension one, are quantities implicitly defined in a manner that prevents their aggregation into unit of measurement, units of measurement. ISBN 978-92-822-2272-0. Typically expressed as ratios that align with another system, these quantities do not necessitate explicitly defined Unit of measurement, units. For instance, alcohol by volume (ABV) represents a volumetric ratio; its value remains independent of the specific Unit of volume, units of volume used, such as in milliliters per milliliter (mL/mL). The 1, number one is recognized as a dimensionless Base unit of measurement, base quantity. Radians serve as dimensionless units for Angle, angular measurements, derived from the universal ratio of 2π times the radius of a circle being equal to its circumference. Dimensionless quantities play a crucial role serving as parameters in differential equations in various technical disciplines. In calculus, concepts like the unitless ratios ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |