Spherical sector

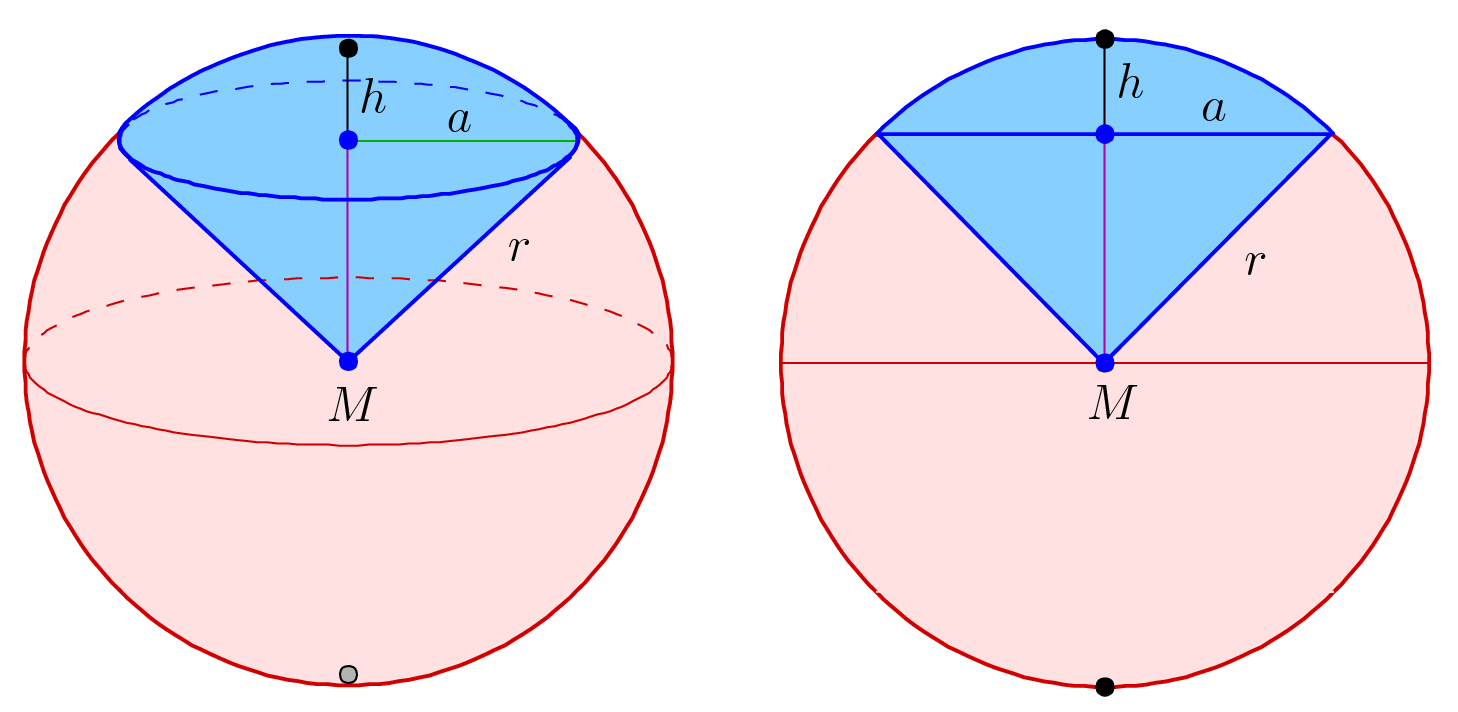
In geometry, a spherical sector, also known as a spherical cone, is a portion of a sphere or of a ball defined by a conical boundary with apex at the center of the sphere. It can be described as the union of a spherical cap and the cone formed by the center of the sphere and the base of the cap. It is the three-dimensional analogue of the sector of a circle.

Volume

If the radius of the sphere is denoted by and the height of the cap by , the volume of the spherical sector is
$V = \frac\,.$

This may also be written as
$V = \frac (1-\cos\varphi)\,,$
where is half the cone aperture angle, i.e., is the angle between the rim of the cap and the axis direction to the middle of the cap as seen from the sphere center. The limiting case is for approaching 180 degrees, which then describes a complete sphere.

The height, is given by
$h = r (1-\cos\varphi)\,.$

The volume of the sector is related to the area of the cap by:
$V = \frac\,.$

Area

The curved surface area of the spherical sector (on the surface of the sphere, excluding the cone surface) is
$A = 2\pi rh\,.$

It is also
$A = \Omega r^2$
where is the solid angle of the spherical sector in steradians, the SI unit of solid angle. One steradian is defined as the solid angle subtended by a cap area of .

Derivation

The volume can be calculated by integrating the differential volume element
$dV = \rho^2 \sin \phi \, d\rho \, d\phi \, d\theta$
over the volume of the spherical sector,
$V = \int_0^ \int_0^\varphi\int_0^r\rho^2\sin\phi \, d\rho \, d\phi \, d\theta = \int_0^ d\theta \int_0^\varphi \sin\phi \, d\phi \int_0^r \rho^2 d\rho = \frac (1-\cos\varphi) \, ,$
where the integrals have been separated, because the integrand can be separated into a product of functions each with one dummy variable.

The area can be similarly calculated by integrating the differential spherical area element
$dA = r^2 \sin\phi \, d\phi \, d\theta$
over the spherical sector, giving
$A = \int_0^ \int_0^\varphi r^2 \sin\phi \, d\phi \, d\theta = r^2 \int_0^ d\theta \int_0^\varphi \sin\phi \, d\phi = 2\pi r^2(1-\cos\varphi) \, ,$
where is inclination (or elevation) and is azimuth (right). Notice is a constant. Again, the integrals can be separated.

See also

* Circular sector — the analogous 2D figure.
* Spherical cap
* Spherical segment
* Spherical wedge

References

Spherical geometry

{{geometry-stub