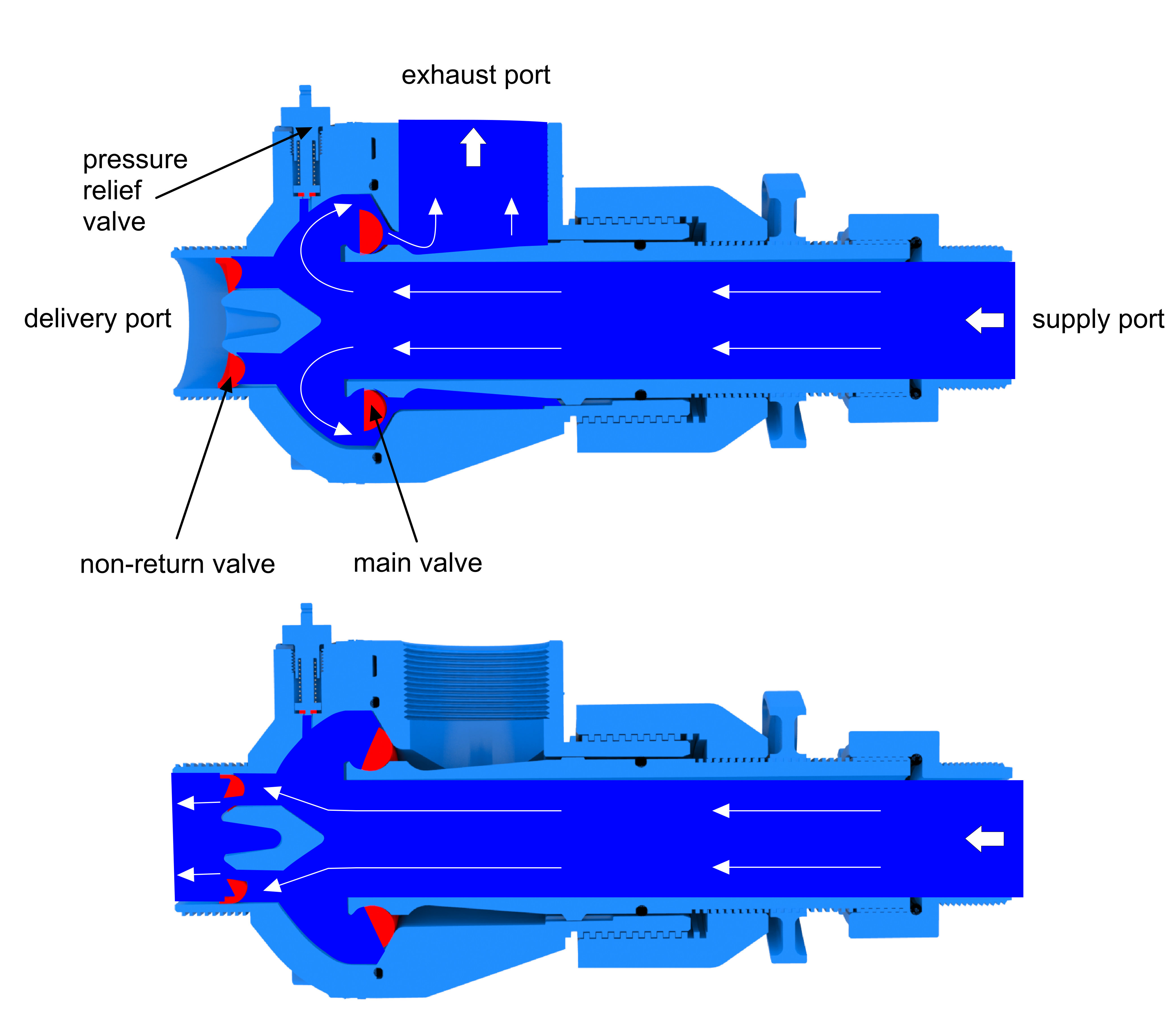
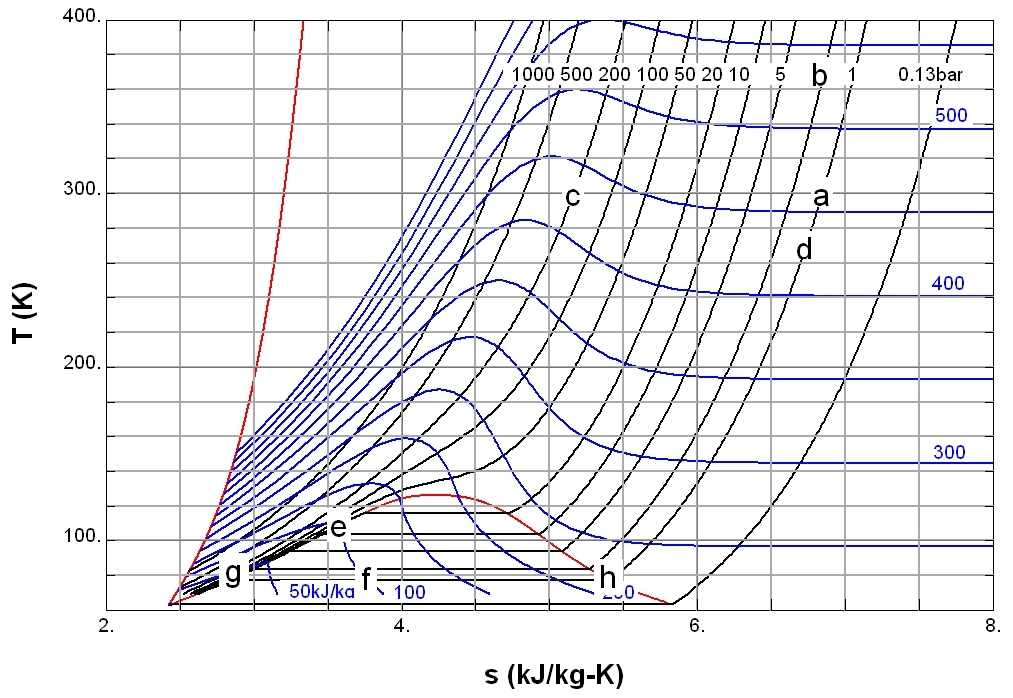
|
Stagnation Pressure
In fluid dynamics, stagnation pressure, also referred to as total pressure, is what the pressure would be if all the kinetic energy of the fluid were to be converted into pressure in a reversable manner.; it is defined as the sum of the free-stream static pressure and the free-stream dynamic pressure. The Bernoulli equation applicable to incompressible flow shows that the stagnation pressure is equal to the dynamic pressure and static pressure combined.Clancy, L.J. (1975), ''Aerodynamics'', Pitman Publishing Limited, London. In compressible flows, stagnation pressure is also equal to total pressure as well, provided that the fluid entering the stagnation point is brought to rest Isentropic flow, isentropically. Stagnation pressure is sometimes referred to as pitot pressure because the two pressures are equal. Magnitude The magnitude of stagnation pressure can be derived from Bernoulli's principle, Bernoulli equation for incompressible flow and no height changes. For any two po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion) and (the study of water and other liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moment (physics), moments on aircraft, determining the mass flow rate of petroleum through pipeline transport, pipelines, weather forecasting, predicting weather patterns, understanding nebulae in interstellar space, understanding large scale Geophysical fluid dynamics, geophysical flows involving oceans/atmosphere and Nuclear weapon design, modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isentropic Process
An isentropic process is an idealized thermodynamic process that is both Adiabatic process, adiabatic and Reversible process (thermodynamics), reversible. The work (physics), work transfers of the system are friction, frictionless, and there is no net transfer of heat or matter. Such an idealized process is useful in engineering as a model of and basis of comparison for real processes. This process is idealized because reversible processes do not occur in reality; thinking of a process as both adiabatic and reversible would show that the initial and final entropies are the same, thus, the reason it is called isentropic (entropy does not change). Thermodynamics, Thermodynamic processes are named based on the effect they would have on the system (ex. isovolumetric: constant volume, isenthalpic: constant enthalpy). Even though in reality it is not necessarily possible to carry out an isentropic process, some may be approximated as such. The word "isentropic" derives from the proc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stagnation Temperature
In thermodynamics and fluid mechanics, stagnation temperature is the temperature at a stagnation point in a fluid flow. At a stagnation point, the speed of the fluid is zero and all of the kinetic energy has been converted to internal energy and is added to the local static enthalpy. In both compressible and incompressible fluid flow, the stagnation temperature equals the ''total temperature'' at all points on the streamline leading to the stagnation point. See gas dynamics. Derivation Adiabatic Stagnation temperature can be derived from the first law of thermodynamics. Applying the steady flow energy equation and ignoring the work, heat and gravitational potential energy terms, we have: :h_0 = h + \frac\, where: :h_0 =\, mass-specific stagnation (or total) enthalpy at a stagnation point :h =\, mass-specific static enthalpy at the point of interest along the stagnation streamline :V =\, velocity at the point of interest along the stagnation streamline Substituting for entha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydraulic Ram
A hydraulic ram pump, ram pump, or hydram is a cyclic pump, cyclic water pump powered by hydropower. It takes in water at one "hydraulic head" (pressure) and flow rate, and outputs water at a higher hydraulic head and lower flow rate. The device uses the water hammer effect to develop pressure that allows a portion of the input water that powers the pump to be lifted to a point higher than where the water originally started. The hydraulic ram is sometimes used in remote areas, where there is both a source of Low head hydro power, low-head hydropower and a need for pumping water to a destination higher in elevation than the source. In this situation, the ram is often useful, since it requires no outside source of Power (physics), power other than the kinetic energy of flowing water. History In 1772, John Whitehurst of Cheshire, England, invented a manually controlled precursor of the hydraulic ram called the "pulsation engine" and installed the first one at Oulton, Cheshir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Gas
In physics, engineering, and physical chemistry, a perfect gas is a theoretical gas model that differs from real gases in specific ways that makes certain calculations easier to handle. In all perfect gas models, intermolecular forces are neglected. This means that one can neglect many complications that may arise from the Van der Waals forces. All perfect gas models are ideal gas models in the sense that they all follow the ideal gas equation of state. However, the idea of a perfect gas model is often invoked as a combination of the ideal gas equation of state with specific additional assumptions regarding the variation (or nonvariation) of the heat capacity with temperature. Perfect gas nomenclature The terms ''perfect gas'' and ''ideal gas'' are sometimes used interchangeably, depending on the particular field of physics and engineering. Sometimes, other distinctions are made, such as between ''thermally perfect gas'' and ''calorically perfect gas'', or between imperfect, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Capacity Ratio
In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace's coefficient, is the ratio of the heat capacity at constant pressure () to heat capacity at constant volume (). It is sometimes also known as the '' isentropic expansion factor'' and is denoted by (gamma) for an ideal gasγ first appeared in an article by the French mathematician, engineer, and physicist Siméon Denis Poisson: * On p. 332, Poisson defines γ merely as a small deviation from equilibrium which causes small variations of the equilibrium value of the density ρ. In Poisson's article of 1823 – * γ was expressed as a function of density D (p. 8) or of pressure P (p. 9). Meanwhile, in 1816 the French mathematician and physicist Pierre-Simon Laplace had found that the speed of sound depends on the ratio of the specific heats. * However, he didn't denote the ratio as γ. In 1825, Laplace stated that the speed of sound i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isentropic
An isentropic process is an idealized thermodynamic process that is both adiabatic and reversible. The work transfers of the system are frictionless, and there is no net transfer of heat or matter. Such an idealized process is useful in engineering as a model of and basis of comparison for real processes. This process is idealized because reversible processes do not occur in reality; thinking of a process as both adiabatic and reversible would show that the initial and final entropies are the same, thus, the reason it is called isentropic (entropy does not change). Thermodynamic processes are named based on the effect they would have on the system (ex. isovolumetric: constant volume, isenthalpic: constant enthalpy). Even though in reality it is not necessarily possible to carry out an isentropic process, some may be approximated as such. The word "isentropic" derives from the process being one in which the entropy of the system remains unchanged. In addition to a process wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mach Number
The Mach number (M or Ma), often only Mach, (; ) is a dimensionless quantity in fluid dynamics representing the ratio of flow velocity past a boundary to the local speed of sound. It is named after the Austrian physicist and philosopher Ernst Mach. \mathrm = \frac, where: * is the local Mach number, * is the local flow velocity with respect to the boundaries (either internal, such as an object immersed in the flow, or external, like a channel), and * is the speed of sound in the medium, which in air varies with the square root of the thermodynamic temperature. By definition, at Mach1, the local flow velocity is equal to the speed of sound. At Mach0.65, is 65% of the speed of sound (subsonic), and, at Mach1.35, is 35% faster than the speed of sound (supersonic). The local speed of sound, and hence the Mach number, depends on the temperature of the surrounding gas. The Mach number is primarily used to determine the approximation with which a flow can be treated as an i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stagnation Temperature
In thermodynamics and fluid mechanics, stagnation temperature is the temperature at a stagnation point in a fluid flow. At a stagnation point, the speed of the fluid is zero and all of the kinetic energy has been converted to internal energy and is added to the local static enthalpy. In both compressible and incompressible fluid flow, the stagnation temperature equals the ''total temperature'' at all points on the streamline leading to the stagnation point. See gas dynamics. Derivation Adiabatic Stagnation temperature can be derived from the first law of thermodynamics. Applying the steady flow energy equation and ignoring the work, heat and gravitational potential energy terms, we have: :h_0 = h + \frac\, where: :h_0 =\, mass-specific stagnation (or total) enthalpy at a stagnation point :h =\, mass-specific static enthalpy at the point of interest along the stagnation streamline :V =\, velocity at the point of interest along the stagnation streamline Substituting for entha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Static Pressure
In fluid mechanics the term static pressure refers to a term in Bernoulli's equation written words as ''static pressure + dynamic pressure = total pressure''. Since pressure measurements at any single point in a fluid always give the static pressure value, the 'static' is often dropped. In the design and operation of aircraft, ''static pressure'' is the air pressure in the aircraft's static pressure system. Static pressure in fluid dynamics The concept of pressure is central to the study of fluids. A pressure can be identified for every point in a body of fluid, regardless of whether the fluid is in motion. Pressure can be measured using an aneroid, Bourdon tube, mercury column, or various other methods. The concepts of ''total pressure'' and '' dynamic pressure'' arise from Bernoulli's equation and are significant in the study of all fluid flows. These two pressures are not pressures in the usual sense - they cannot be measured using a pressure sensor. To avoid potential ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enthalpy
Enthalpy () is the sum of a thermodynamic system's internal energy and the product of its pressure and volume. It is a state function in thermodynamics used in many measurements in chemical, biological, and physical systems at a constant external pressure, which is conveniently provided by the large ambient atmosphere. The pressure–volume term expresses the work (physics), work W that was done against constant external pressure P_\text to establish the system's physical dimensions from V_\text=0 to some final volume V_\text (as W=P_\text\Delta V), i.e. to make room for it by displacing its surroundings. The pressure-volume term is very small for solids and liquids at common conditions, and fairly small for gases. Therefore, enthalpy is a stand-in for energy in chemical systems; Bond energy, bond, Lattice energy, lattice, solvation, and other chemical "energies" are actually enthalpy differences. As a state function, enthalpy depends only on the final configuration of internal e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli's Principle
Bernoulli's principle is a key concept in fluid dynamics that relates pressure, speed and height. For example, for a fluid flowing horizontally Bernoulli's principle states that an increase in the speed occurs simultaneously with a decrease in static pressure, pressure The principle is named after the Swiss mathematician and physicist Daniel Bernoulli, who published it in his book ''Hydrodynamica'' in 1738. Although Bernoulli deduced that pressure decreases when the flow speed increases, it was Leonhard Euler in 1752 who derived Bernoulli's equation in its usual form. Bernoulli's principle can be derived from the principle of conservation of energy. This states that, in a steady flow, the sum of all forms of energy in a fluid is the same at all points that are free of viscous forces. This requires that the sum of kinetic energy, potential energy and internal energy remains constant. Thus an increase in the speed of the fluid—implying an increase in its kinetic energy—occur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |