|
Spinodal
In thermodynamics, the limit of local stability against phase separation with respect to small fluctuations is clearly defined by the condition that the second derivative of Gibbs free energy is zero. : 0 The locus of these points (the inflection point within a G-x or G-c curve, Gibbs free energy as a function of composition) is known as the spinodal curve.G. Astarita: ''Thermodynamics: An Advanced Textbook for Chemical Engineers'' (Springer 1990), chaps 4, 8, 9, 12.Sandler S. I., ''Chemical and Engineering Thermodynamics''. 1999 John Wiley & Sons, Inc., p 571.Koningsveld K., Stockmayer W. H., Nies, E., ''Polymer Phase Diagrams: A Textbook''. 2001 Oxford, p 12. For compositions within this curve, infinitesimally small fluctuations in composition and density will lead to phase separation via spinodal decomposition. Outside of the curve, the solution will be at least metastable with respect to fluctuations. In other words, outside the spinodal curve some careful process may obtain ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spinodal Decomposition
Spinodal decomposition is a mechanism by which a single thermodynamic Phase (matter), phase spontaneously separates into two phases (without nucleation). Decomposition occurs when there is no Thermodynamics, thermodynamic barrier to phase separation. As a result, phase separation via decomposition does not require the nucleation events resulting from thermodynamic fluctuations, which normally trigger phase separation. Spinodal decomposition is observed when mixtures of metals or polymers separate into two co-existing phases, each rich in one species and poor in the other. When the two phases emerge in approximately equal proportion (each occupying about the same volume or area), characteristic intertwined structures are formed that gradually coarsen (see animation). The dynamics of spinodal decomposition is commonly modeled using the Cahn–Hilliard equation. Spinodal decomposition is fundamentally different from nucleation and growth. When there is a nucleation barrier to the form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs Free Energy
In thermodynamics, the Gibbs free energy (or Gibbs energy as the recommended name; symbol is a thermodynamic potential that can be used to calculate the maximum amount of Work (thermodynamics), work, other than Work (thermodynamics)#Pressure–volume work, pressure–volume work, that may be performed by a closed system, thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions. The Gibbs free energy is expressed as G(p,T) = U + pV - TS = H - TS where: * U is the internal energy of the system * H is the enthalpy of the system * S is the entropy of the system * T is the temperature of the system * V is the volume of the system * p is the pressure of the system (which must be equal to that of the surroundings for mechanical equilibrium). The Gibbs free energy change (, measured in joules in International System of Units, SI) is the ''maximum'' amount of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Miscibility Gap
A miscibility gap is a region in a phase diagram for a mixture In chemistry, a mixture is a material made up of two or more different chemical substances which can be separated by physical method. It is an impure substance made up of 2 or more elements or compounds mechanically mixed together in any proporti ... of components where the mixture exists as two or more phases – any region of composition of mixtures where the constituents are not completely miscible. The IUPAC Gold Book defines ''miscibility gap'' as "Area within the coexistence curve of an isobaric phase diagram (temperature vs composition) or an isothermal phase diagram (pressure vs composition)." A miscibility gap between isostructural phases may be described as the '' solvus'', a term also used to describe the boundary on a phase diagram between a miscibility gap and other phases. Thermodynamically, miscibility gaps indicate a maximum (''e.g.'' of Gibbs energy) in the composition range. The miscibility ga ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Field Theory
In physics and probability theory, Mean-field theory (MFT) or Self-consistent field theory studies the behavior of high-dimensional random (stochastic) models by studying a simpler model that approximates the original by averaging over degrees of freedom (the number of values in the final calculation of a statistic that are free to vary). Such models consider many individual components that interact with each other. The main idea of MFT is to replace all interactions to any one body with an average or effective interaction, sometimes called a ''molecular field''. This reduces any many-body problem into an effective one-body problem. The ease of solving MFT problems means that some insight into the behavior of the system can be obtained at a lower computational cost. MFT has since been applied to a wide range of fields outside of physics, including statistical inference, graphical models, neuroscience, artificial intelligence, epidemic models, queueing theory, computer-network ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Critical Exponent
Critical exponents describe the behavior of physical quantities near continuous phase transitions. It is believed, though not proven, that they are universal, i.e. they do not depend on the details of the physical system, but only on some of its general features. For instance, for ferromagnetic systems at thermal equilibrium, the critical exponents depend only on: * the dimension of the system * the range of the interaction * the spin dimension These properties of critical exponents are supported by experimental data. Analytical results can be theoretically achieved in mean field theory in high dimensions or when exact solutions are known such as the two-dimensional Ising model. The theoretical treatment in generic dimensions requires the renormalization group approach or, for systems at thermal equilibrium, the conformal bootstrap techniques. Phase transitions and critical exponents appear in many physical systems such as water at the critical point, in magnetic systems, in supe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
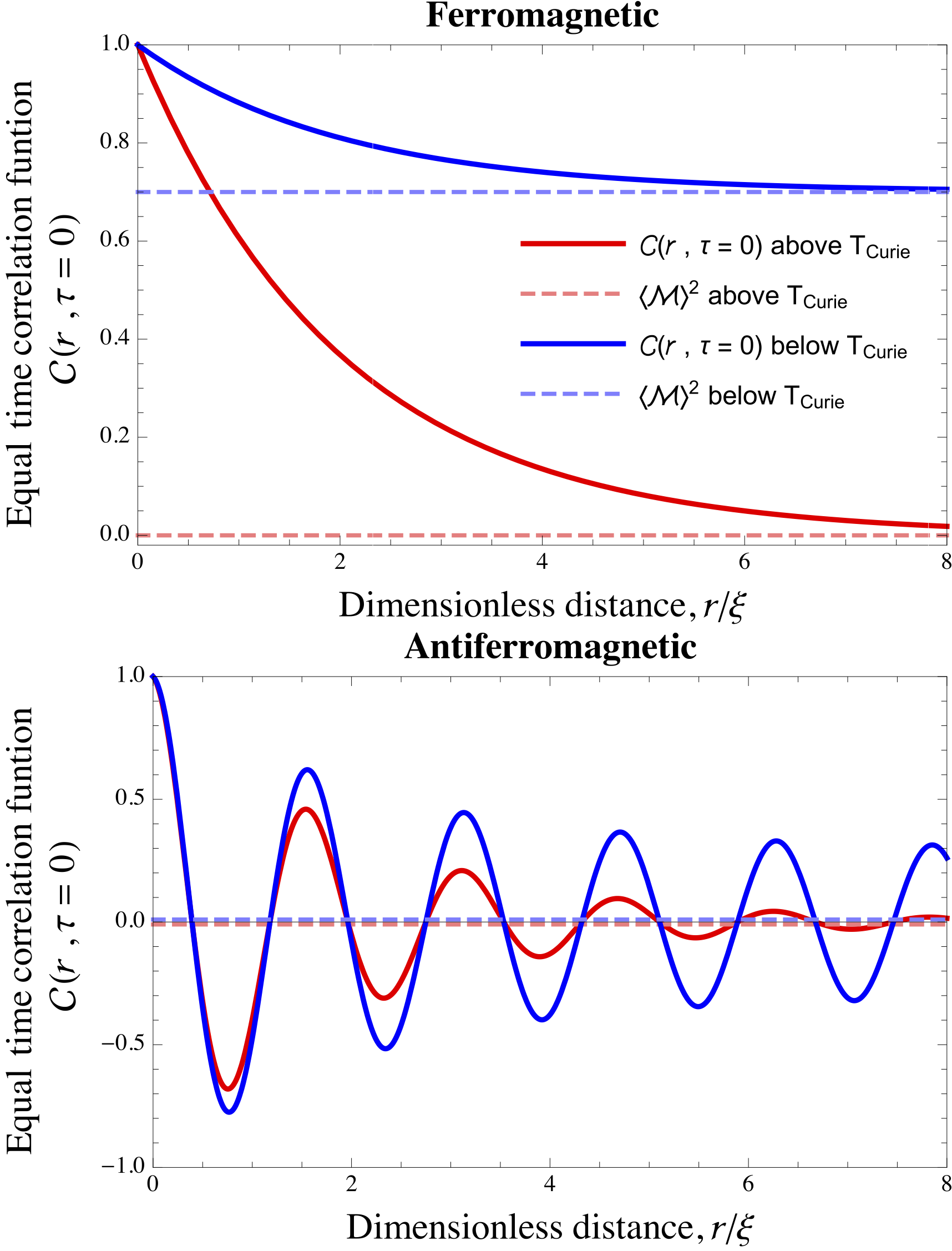
Correlation Function (statistical Mechanics)
In statistical mechanics, the correlation function is a measure of the order in a system, as characterized by a mathematical correlation function. Correlation functions describe how microscopic variables, such as spin and density, at different positions or times are related. More specifically, correlation functions measure quantitatively the extent to which microscopic variables fluctuate together, on average, across space and/or time. Keep in mind that correlation doesn’t automatically equate to causation. So, even if there’s a non-zero correlation between two points in space or time, it doesn’t mean there is a direct causal link between them. Sometimes, a correlation can exist without any causal relationship. This could be purely coincidental or due to other underlying factors, known as confounding variables, which cause both points to covary (statistically). A classic example of spatial correlation can be seen in ferromagnetic and antiferromagnetic materials. In these ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Critical Point (thermodynamics)
In thermodynamics, a critical point (or critical state) is the end point of a phase Equilibrium (thermodynamics), equilibrium curve. One example is the liquid–vapor critical point, the end point of the pressure–temperature curve that designates conditions under which a liquid and its vapor can coexist. At higher temperatures, the gas comes into a supercritical fluid, supercritical phase, and so cannot be liquefied by pressure alone. At the critical point, defined by a ''critical temperature'' ''T''c and a ''critical pressure'' ''p''c, phase (matter), phase boundaries vanish. Other examples include the Upper critical solution temperature, liquid–liquid critical points in mixtures, and the ferromagnet–paramagnet transition (Curie temperature) in the absence of an external magnetic field. Liquid–vapor critical point Overview For simplicity and clarity, the generic notion of ''critical point'' is best introduced by discussing a specific example, the vapor–liquid cr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Upper Critical Solution Temperature
The upper critical solution temperature (UCST) or upper consolute temperature is the critical temperature above which the components of a mixture are miscible in all proportions. The word ''upper'' indicates that the UCST is an upper bound to a temperature range of partial miscibility, or miscibility for certain compositions only. For example, hexane-nitrobenzene mixtures have a UCST of , so that these two substances are miscible in all proportions above but not at lower temperatures. Examples at higher temperatures are the aniline-water system at (at pressures high enough for liquid water to exist at that temperature), and the lead-zinc system at (a temperature where both metals are liquid). A solid state example is the palladium-hydrogen system which has a solid solution phase (H2 in Pd) in equilibrium with a hydride phase (PdHn) below the UCST at 300 °C. Above this temperature there is a single solid solution phase. In the phase diagram of the mixture components, the U ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Vapor Deposition
Physical vapor deposition (PVD), sometimes called physical vapor transport (PVT), describes a variety of vacuum deposition methods which can be used to produce thin films and coatings on substrates including metals, ceramics, glass, and polymers. PVD is characterized by a process in which the material transitions from a condensed phase to a vapor phase and then back to a thin film condensed phase. The most common PVD processes are Sputter coating, sputtering and Evaporation (deposition), evaporation. PVD is used in the manufacturing of items which require thin films for optical, mechanical, electrical, acoustic or chemical functions. Examples include semiconductor devices such as thin-film solar cells, microelectromechanical devices such as thin film bulk acoustic resonator, aluminized Polyethylene terephthalate, PET film for food packaging and balloons, and titanium nitride coated cutting tools for metalworking. Besides PVD tools for fabrication, special smaller tools used mai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binodal
In thermodynamics, the binodal, also known as the coexistence curve or binodal curve, denotes the state of a multi-component system at which the system's distinct phases straddle between coexistence or miscibility. Equivalently, it is the boundary on which thermodynamics favors the system components to dissolve or separate into two phases.IUPAC binodal curve definition http://old.iupac.org/goldbook/BT07273.pdf accessed 2/20/13 In general, the binodal is defined by the condition at which the chemical potential of all solution components is equal in each phase. The extremum of a binodal curve in temperature coincides with the extremum of the spinodal In thermodynamics, the limit of local stability against phase separation with respect to small fluctuations is clearly defined by the condition that the second derivative of Gibbs free energy is zero. : 0 The locus of these points (the inflecti ... curve, and is known as a critical point. Binary systems In binary (two compon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamics
Thermodynamics is a branch of physics that deals with heat, Work (thermodynamics), work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of thermodynamics, which convey a quantitative description using measurable macroscopic physical quantity, physical quantities but may be explained in terms of microscopic constituents by statistical mechanics. Thermodynamics applies to various topics in science and engineering, especially physical chemistry, biochemistry, chemical engineering, and mechanical engineering, as well as other complex fields such as meteorology. Historically, thermodynamics developed out of a desire to increase the thermodynamic efficiency, efficiency of early steam engines, particularly through the work of French physicist Nicolas Léonard Sadi Carnot, Sadi Carnot (1824) who believed that engine efficiency was the key that could help France win ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |