|
Spheroid
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface (mathematics), surface obtained by Surface of revolution, rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry. If the ellipse is rotated about its major axis, the result is a ''prolate spheroid'', elongated like a rugby ball. The ball (gridiron football), American football is similar but has a pointier end than a spheroid could. If the ellipse is rotated about its minor axis, the result is an ''oblate spheroid'', flattened like a lentil or a plain M&M's, M&M. If the generating ellipse is a circle, the result is a sphere. Due to the combined effects of gravity and rotation of the Earth, rotation, the figure of the Earth (and of all planets) is not quite a sphere, but instead is slightly flattening, flattened in the direction of its axis of rotation. For that reason, in cartography and geode ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipsoid
An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional Scaling (geometry), scalings, or more generally, of an affine transformation. An ellipsoid is a quadric surface; that is, a Surface (mathematics), surface that may be defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, an ellipsoid is characterized by either of the two following properties. Every planar Cross section (geometry), cross section is either an ellipse, or is empty, or is reduced to a single point (this explains the name, meaning "ellipse-like"). It is Bounded set, bounded, which means that it may be enclosed in a sufficiently large sphere. An ellipsoid has three pairwise perpendicular Rotational symmetry, axes of symmetry which intersect at a Central symmetry, center of symmetry, called the center of the ellipsoid. The line segments that are delimited on the axes of symmetry by the ellipsoid are called the ''principal ax ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadric
In mathematics, a quadric or quadric surface is a generalization of conic sections (ellipses, parabolas, and hyperbolas). In three-dimensional space, quadrics include ellipsoids, paraboloids, and hyperboloids. More generally, a quadric hypersurface (of dimension ''D'') embedded in a higher dimensional space (of dimension ) is defined as the zero set of an irreducible polynomial of degree two in variables; for example, ''D''1 is the case of conic sections ( plane curves). When the defining polynomial is not absolutely irreducible, the zero set is generally not considered a quadric, although it is often called a ''degenerate quadric'' or a ''reducible quadric''. A quadric is an affine algebraic variety, or, if it is reducible, an affine algebraic set. Quadrics may also be defined in projective spaces; see , below. Formulation In coordinates , the general quadric is thus defined by the algebraic equationSilvio LevQuadricsin "Geometry Formulas and Facts", excerpted from 3 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
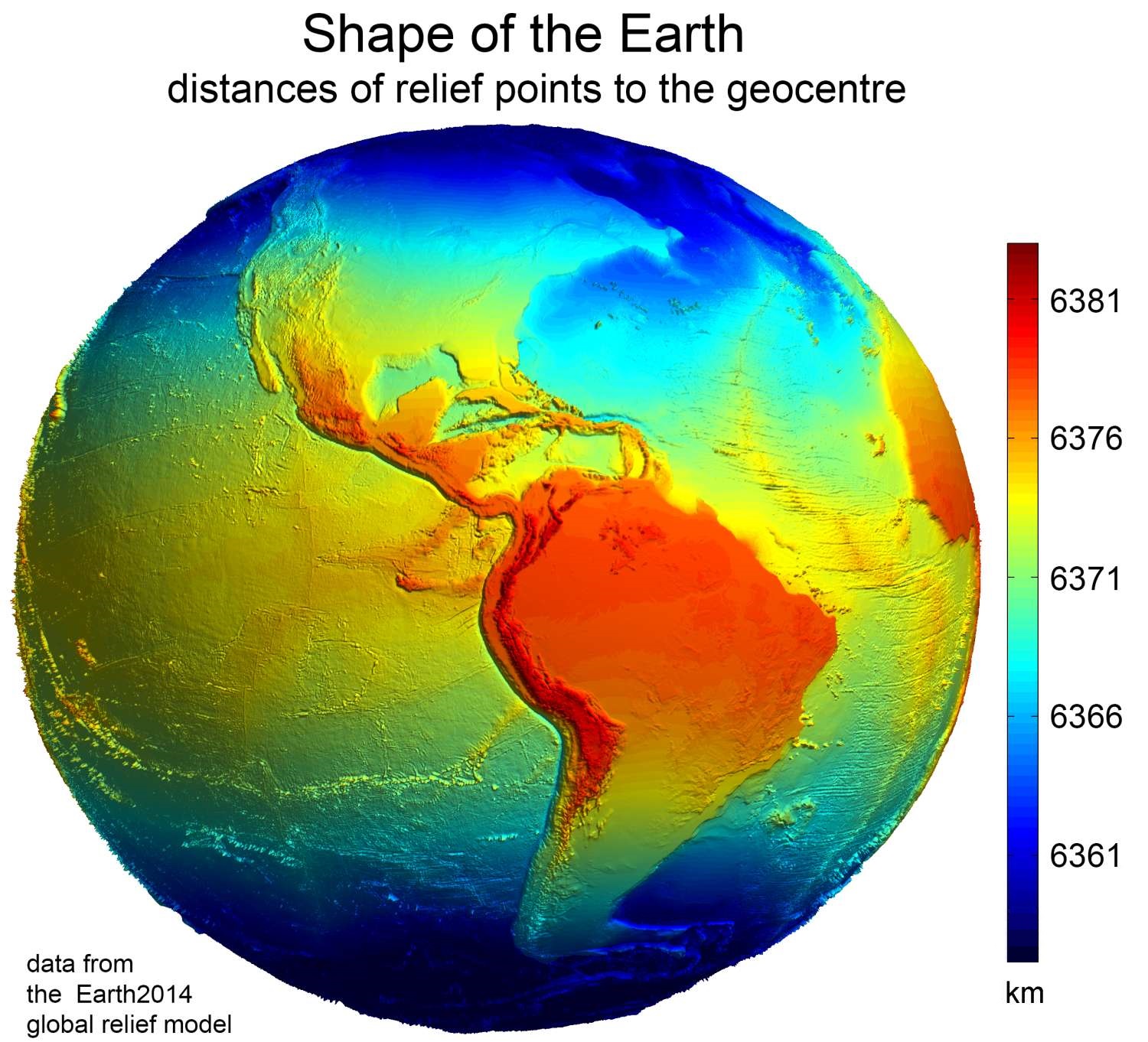
Reference Ellipsoid
An Earth ellipsoid or Earth spheroid is a mathematical figure approximating the Earth's form, used as a reference frame for computations in geodesy, astronomy, and the geosciences. Various different ellipsoids have been used as approximations. It is a spheroid (an ellipsoid of revolution) whose minor axis (shorter diameter), which connects the geographical North Pole and South Pole, is approximately aligned with the Earth's axis of rotation. The ellipsoid is defined by the ''equatorial axis'' () and the ''polar axis'' (); their radial difference is slightly more than 21 km, or 0.335% of (which is not quite 6,400 km). Many methods exist for determination of the axes of an Earth ellipsoid, ranging from meridian arcs up to modern satellite geodesy or the analysis and interconnection of continental geodetic networks. Amongst the different set of data used in national surveys are several of special importance: the Bessel ellipsoid of 1841, the international Hayfo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Figure Of The Earth
In geodesy, the figure of the Earth is the size and shape used to model planet Earth. The kind of figure depends on application, including the precision needed for the model. A spherical Earth is a well-known historical approximation that is satisfactory for geography, astronomy and many other purposes. Several models with greater accuracy (including ellipsoid) have been developed so that coordinate systems can serve the precise needs of navigation, surveying, cadastre, land use, and various other concerns. Motivation Earth's topographic surface is apparent with its variety of land forms and water areas. This topographic surface is generally the concern of topographers, hydrographers, and geophysicists. While it is the surface on which Earth measurements are made, mathematically modeling it while taking the irregularities into account would be extremely complicated. The Pythagorean concept of a spherical Earth offers a simple surface that is easy to deal with mathem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Of Revolution
A surface of revolution is a Surface (mathematics), surface in Euclidean space created by rotating a curve (the ''generatrix'') one full revolution (unit), revolution around an ''axis of rotation'' (normally not Intersection (geometry), intersecting the generatrix, except at its endpoints). The volume bounded by the surface created by this revolution is the ''solid of revolution''. Examples of surfaces of revolution generated by a straight line are cylinder (geometry), cylindrical and conical surfaces depending on whether or not the line is parallel to the axis. A circle that is rotated around any diameter generates a sphere of which it is then a great circle, and if the circle is rotated around an axis that does not intersect the interior of a circle, then it generates a torus which does not intersect itself (a ring torus). Properties The sections of the surface of revolution made by planes through the axis are called ''meridional sections''. Any meridional section can be consi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity (mathematics), eccentricity e, a number ranging from e = 0 (the Limiting case (mathematics), limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but for Perimeter of an ellipse, its perimeter (also known as circumference), Integral, integration is required to obtain an exact solution. The largest and smallest diameters of an ellipse, also known as its width and height, are typically denoted and . An ellipse has four extreme points: two ''Vertex (geometry), vertices'' at the endpoints of the major axis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Walter De Gruyter
Walter de Gruyter GmbH, known as De Gruyter (), is a German scholarly publishing house specializing in academic literature. History The roots of the company go back to 1749 when Frederick the Great granted the Königliche Realschule in Berlin the royal privilege to open a bookstore and "to publish good and useful books". In 1800, the store was taken over by Georg Reimer (1776–1842), operating as the ''Reimer'sche Buchhandlung'' from 1817, while the school's press eventually became the ''Georg Reimer Verlag''. From 1816, Reimer used a representative palace at Wilhelmstraße 73 in Berlin for his family and the publishing house, whereby the wings contained his print shop and press. The building later served as the Palace of the Reich President. Born in Ruhrort in 1862, Walter de Gruyter took a position with Reimer Verlag in 1894. By 1897, at the age of 35, he had become sole proprietor of the hundred-year-old company then known for publishing the works of German romantic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geopotential Model
In geophysics and physical geodesy, a geopotential model is the theoretical analysis of measuring and calculating the effects of Earth's gravitational field (the geopotential). The Earth is not exactly spherical, mainly because of its rotation around the polar axis that makes its shape slightly oblate. However, a spherical harmonics series expansion captures the actual field with increasing fidelity. If Earth's shape were perfectly known together with the exact mass density ρ = ρ(''x'', ''y'', ''z''), it could be integrated numerically (when combined with a reciprocal distance kernel) to find an accurate model for Earth's gravitational field. However, the situation is in fact the opposite: by observing the orbits of spacecraft and the Moon, Earth's gravitational field can be determined quite accurately. The best estimate of Earth's mass is obtained by dividing the product ''GM'' as determined from the analysis of spacecraft orbit with a value for the gravitational constant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flattening
Flattening is a measure of the compression of a circle or sphere along a diameter to form an ellipse or an ellipsoid of revolution (spheroid) respectively. Other terms used are ellipticity, or oblateness. The usual notation for flattening is f and its definition in terms of the semi-major and semi-minor axes, semi-axes a and b of the resulting ellipse or ellipsoid is : f =\frac . The ''compression factor'' is b/a in each case; for the ellipse, this is also its aspect ratio. Definitions There are three variants: the flattening f, sometimes called the ''first flattening'', as well as two other "flattenings" f' and n, each sometimes called the ''second flattening'', sometimes only given a symbol, or sometimes called the ''second flattening'' and ''third flattening'', respectively. In the following, a is the larger dimension (e.g. semimajor axis), whereas b is the smaller (semiminor axis). All flattenings are zero for a circle (). :: Identities The flattenings can be related t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geographical Pole
A geographical pole or geographic pole is either of the two points on Earth where its axis of rotation intersects its surface. The North Pole lies in the Arctic Ocean while the South Pole is in Antarctica. North and South poles are also defined for other planets or satellites in the Solar System, with a North pole being on the same side of the invariable plane as Earth's North pole. Relative to Earth's surface, the geographic poles move by a few metres over periods of a few years. This is a combination of Chandler wobble, a free oscillation with a period of about 433 days; an annual motion responding to seasonal movements of air and water masses; and an irregular drift towards the 80th west meridian (geography), meridian. As cartography requires exact and unchanging coordinates, the averaged locations of geographical poles are taken as fixed ''cartographic poles'' and become the points where the body's great circles of longitude intersect. See also * Earth's rotation * Polar mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |