|
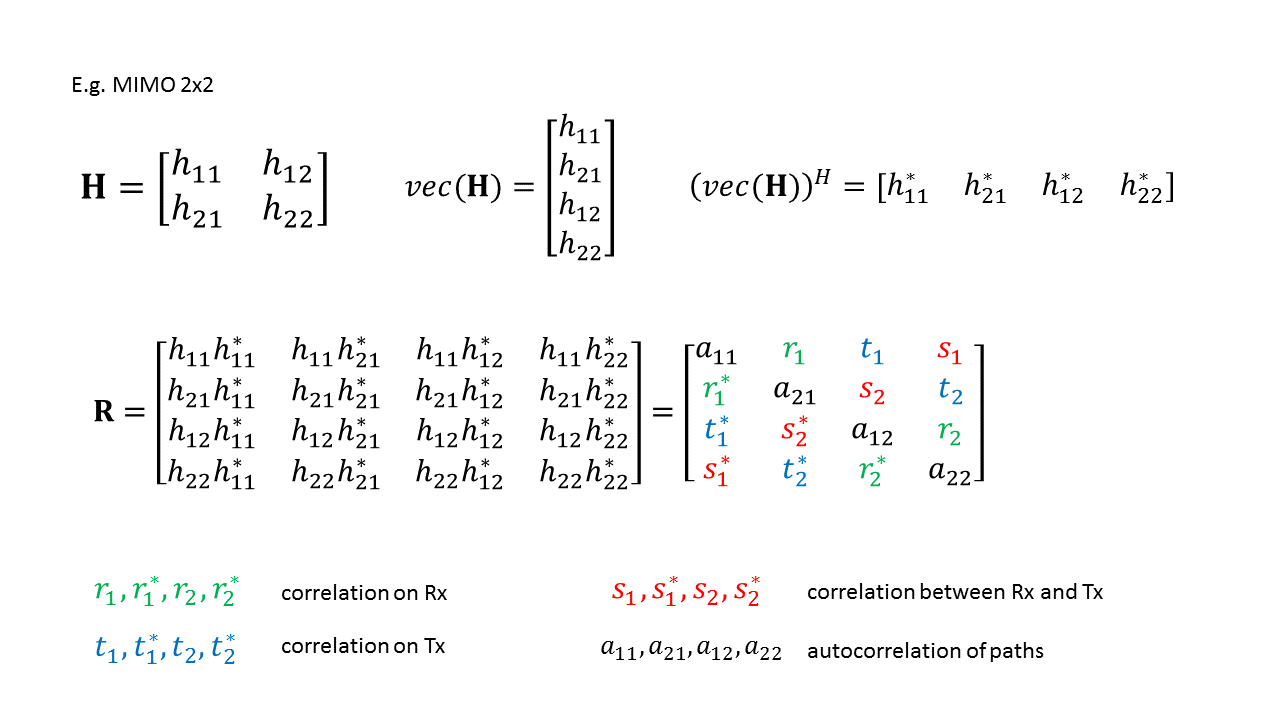
Spatial Correlation
In wireless communication, spatial correlation is the correlation between a signal's spatial direction and the average received signal gain. Theoretically, the performance of wireless communication systems can be improved by having multiple antennas at the transmitter and the receiver. The idea is that if the propagation channels between each pair of transmit and receive antennas are statistically independent and identically distributed, then multiple independent channels with identical characteristics can be created by precoding and be used for either transmitting multiple data streams or increasing the reliability (in terms of bit error rate). In practice, the channels between different antennas are often correlated and therefore the potential multi antenna gains may not always be obtainable. Existence In an ideal communication scenario, there is a line-of-sight path between the transmitter and receiver that represents clear spatial channel characteristics. In urban cell ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wireless Communication
Wireless communication (or just wireless, when the context allows) is the transfer of information (''telecommunication'') between two or more points without the use of an electrical conductor, optical fiber or other continuous guided medium for the transfer. The most common wireless technologies use radio waves. With radio waves, intended distances can be short, such as a few meters for Bluetooth, or as far as millions of kilometers for deep-space radio communications. It encompasses various types of fixed, mobile, and portable applications, including two-way radios, cellular telephones, personal digital assistants (PDAs), and wireless networking. Other examples of applications of radio ''wireless technology'' include GPS units, garage door openers, wireless computer mouse, keyboards and headsets, headphones, radio receivers, satellite television, broadcast television and cordless telephones. Somewhat less common methods of achieving wireless communications in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Narrowband
Narrowband signals are signals that occupy a narrow range of frequencies or that have a small fractional bandwidth. In the audio spectrum, ''narrowband sounds'' are sounds that occupy a narrow range of frequencies. In telephony, narrowband is usually considered to cover frequencies 300–3400 Hz, i.e. the voiceband. In radio communications, a narrowband channel is a channel in which the bandwidth of the message does not significantly exceed the channel's coherence bandwidth. In the study of wired channels, ''narrowband'' implies that the channel under consideration is sufficiently narrow that its frequency response can be considered flat. The message bandwidth will therefore be less than the coherence bandwidth of the channel. That is, no channel has perfectly flat fading, but the analysis of many aspects of wireless systems is greatly simplified if flat fading can be assumed. Two-way radio narrowband Two-Way Radio Narrowbanding refers to a U.S. Federal Communicatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bit Error Rate
In digital transmission, the number of bit errors is the number of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors. The bit error rate (BER) is the number of bit errors per unit time. The bit error ratio (also BER) is the number of bit errors divided by the total number of transferred bits during a studied time interval. Bit error ratio is a unitless performance measure, often expressed as a percentage. The bit error probability ''pe'' is the expected value of the bit error ratio. The bit error ratio can be considered as an approximate estimate of the bit error probability. This estimate is accurate for a long time interval and a high number of bit errors. Example As an example, assume this transmitted bit sequence: 1 1 0 0 0 1 0 1 1 and the following received bit sequence: 0 1 0 1 0 1 0 0 1, The number of bit errors (the underlined bits) is, in this case, 3. The BER is 3 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
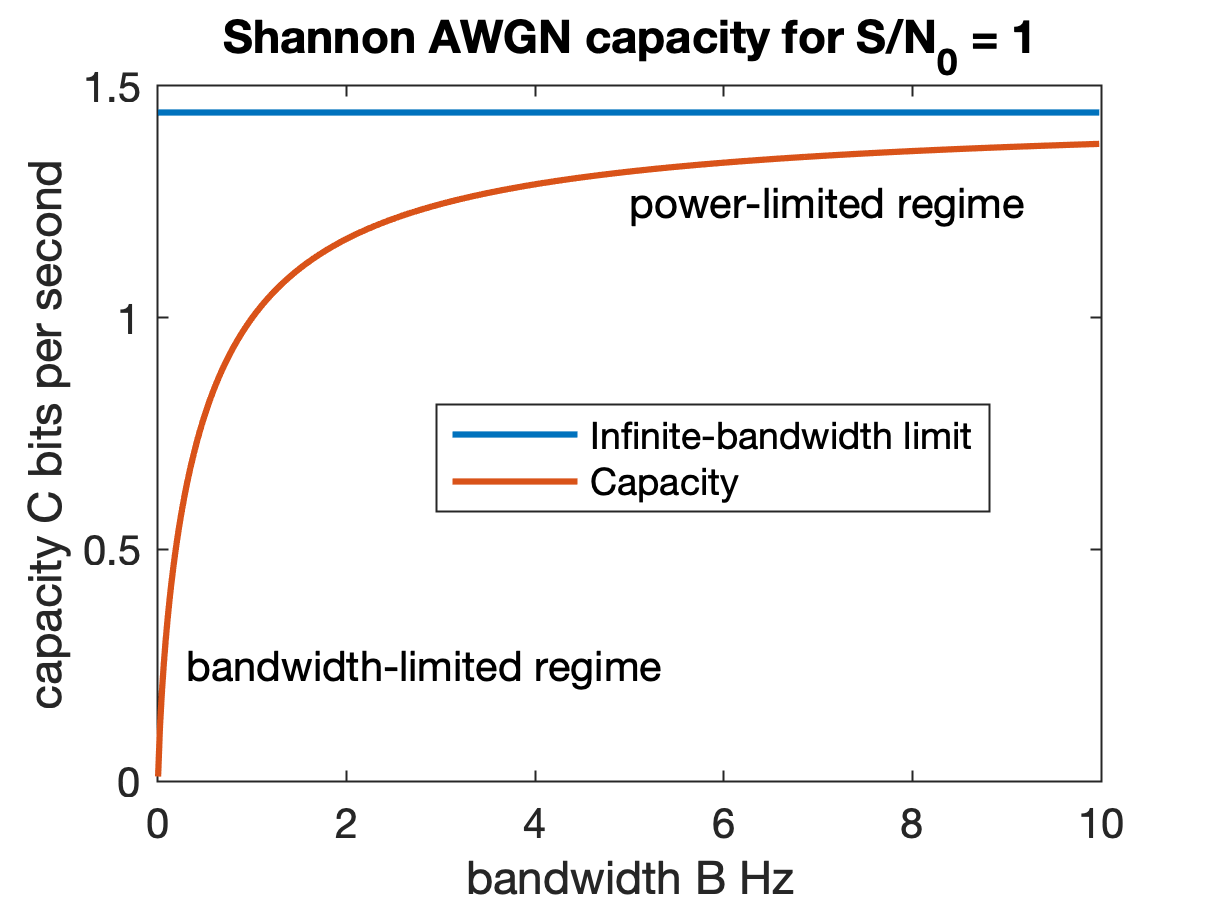
Channel Capacity
Channel capacity, in electrical engineering, computer science, and information theory, is the theoretical maximum rate at which information can be reliably transmitted over a communication channel. Following the terms of the noisy-channel coding theorem, the channel capacity of a given Channel (communications), channel is the highest information rate (in units of information entropy, information per unit time) that can be achieved with arbitrarily small error probability. Information theory, developed by Claude E. Shannon in 1948, defines the notion of channel capacity and provides a mathematical model by which it may be computed. The key result states that the capacity of the channel, as defined above, is given by the maximum of the mutual information between the input and output of the channel, where the maximization is with respect to the input distribution. The notion of channel capacity has been central to the development of modern wireline and wireless communication system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Theory
Information theory is the mathematical study of the quantification (science), quantification, Data storage, storage, and telecommunications, communication of information. The field was established and formalized by Claude Shannon in the 1940s, though early contributions were made in the 1920s through the works of Harry Nyquist and Ralph Hartley. It is at the intersection of electronic engineering, mathematics, statistics, computer science, Neuroscience, neurobiology, physics, and electrical engineering. A key measure in information theory is information entropy, entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a Fair coin, fair coin flip (which has two equally likely outcomes) provides less information (lower entropy, less uncertainty) than identifying the outcome from a roll of a dice, die (which has six equally likely outcomes). Some other important measu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Majorization
In mathematics, majorization is a preorder on vector space, vectors of real numbers. For two such vectors, \mathbf,\ \mathbf \in \mathbb^n, we say that \mathbf weakly majorizes (or dominates) \mathbf from below, commonly denoted \mathbf \succ_w \mathbf, when : \sum_^k x_i^ \geq \sum_^k y_i^ for all k=1,\,\dots,\,n, where x_i^ denotes ith largest entry of x. If \mathbf, \mathbf further satisfy \sum_^n x_i = \sum_^n y_i, we say that \mathbf majorizes (or dominates) \mathbf , commonly denoted \mathbf \succ \mathbf. Both weak majorization and majorization are partially ordered set, partial orders for vectors whose entries are non-decreasing, but only a preorder for general vectors, since majorization is agnostic to the ordering of the entries in vectors, e.g., the statement (1,2)\prec (0,3) is simply equivalent to (2,1)\prec (3,0). Specifically, \mathbf \succ \mathbf \wedge \mathbf \succ \mathbf if and only if \mathbf, \mathbf are permutations of each other. Similarly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalue, Eigenvector And Eigenspace
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a constant factor \lambda when the linear transformation is applied to it: T\mathbf v=\lambda \mathbf v. The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor \lambda (possibly a negative or complex number). Geometrically, vectors are multi-dimensional quantities with magnitude and direction, often pictured as arrows. A linear transformation rotates, stretches, or shears the vectors upon which it acts. A linear transformation's eigenvectors are those vectors that are only stretched or shrunk, with neither rotation nor shear. The corresponding eigenvalue is the factor by which an eigenvector is stretched or shrunk. If the eigenvalue is negative, the eigenvector's direction is reversed. The e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kronecker Product
In mathematics, the Kronecker product, sometimes denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It is a specialization of the tensor product (which is denoted by the same symbol) from vectors to matrices and gives the matrix of the tensor product linear map with respect to a standard choice of basis. The Kronecker product is to be distinguished from the usual matrix multiplication, which is an entirely different operation. The Kronecker product is also sometimes called matrix direct product. The Kronecker product is named after the German mathematician Leopold Kronecker (1823–1891), even though there is little evidence that he was the first to define and use it. The Kronecker product has also been called the ''Zehfuss matrix'', and the ''Zehfuss product'', after , who in 1858 described this matrix operation, but Kronecker product is currently the most widely used term. The misattribution to Kronecker rather than Zehfuss wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Normal Distribution
In probability theory, the family of complex normal distributions, denoted \mathcal or \mathcal_, characterizes complex random variables whose real and imaginary parts are jointly normal. The complex normal family has three parameters: ''location'' parameter ''μ'', ''covariance'' matrix \Gamma, and the ''relation'' matrix C. The standard complex normal is the univariate distribution with \mu = 0, \Gamma=1, and C=0. An important subclass of complex normal family is called the circularly-symmetric (central) complex normal and corresponds to the case of zero relation matrix and zero mean: \mu = 0 and C=0 . This case is used extensively in signal processing, where it is sometimes referred to as just complex normal in the literature. Definitions Complex standard normal random variable The standard complex normal random variable or standard complex Gaussian random variable is a complex random variable Z whose real and imaginary parts are independent normally distributed random v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rayleigh Fading
Rayleigh fading is a statistical model for the effect of a propagation environment on a radio signal, such as that used by wireless devices. Rayleigh fading models assume that the magnitude of a signal that has passed through such a transmission medium (also called a communication channel) will vary randomly, or fade, according to a Rayleigh distribution — the radial component of the sum of two uncorrelated Gaussian random variables. Rayleigh fading is viewed as a reasonable model for tropospheric and ionospheric signal propagation as well as the effect of heavily built-up urban environments on radio signals. Rayleigh fading is most applicable when there is no dominant propagation along a line of sight between the transmitter and receiver. If there is a dominant line of sight, Rician fading may be more applicable. Rayleigh fading is a special case of two-wave with diffuse power (TWDP) fading. The model Rayleigh fading is a reasonable model when there are many objects i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Transpose
In mathematics, the conjugate transpose, also known as the Hermitian transpose, of an m \times n complex matrix \mathbf is an n \times m matrix obtained by transposing \mathbf and applying complex conjugation to each entry (the complex conjugate of a+ib being a-ib, for real numbers a and b). There are several notations, such as \mathbf^\mathrm or \mathbf^*, \mathbf', or (often in physics) \mathbf^. For real matrices, the conjugate transpose is just the transpose, \mathbf^\mathrm = \mathbf^\operatorname. Definition The conjugate transpose of an m \times n matrix \mathbf is formally defined by where the subscript ij denotes the (i,j)-th entry (matrix element), for 1 \le i \le n and 1 \le j \le m, and the overbar denotes a scalar complex conjugate. This definition can also be written as :\mathbf^\mathrm = \left(\overline\right)^\operatorname = \overline where \mathbf^\operatorname denotes the transpose and \overline denotes the matrix with complex conjugated entries. Other na ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |