|
Snellius–Pothenot Problem
In trigonometry, the Snellius–Pothenot problem is a problem first described in the context of planar surveying. Given three known points , an observer at an unknown point observes that the line segment subtends an angle and the segment subtends an angle ; the problem is to determine the position of the point . (See figure; the point denoted is between and as seen from ). Since it involves the observation of known points from an unknown point, the problem is an example of resection. Historically it was first studied by Snellius, who found a solution around 1615. Formulating the equations First equation Denoting the (unknown) angles as and as gives: x+y = 2 \pi - \alpha - \beta - C by using the sum of the angles formula for the quadrilateral . The variable represents the (known) internal angle in this quadrilateral at point . (Note that in the case where the points and are on the same side of the line , the angle will be greater than ). Second equation Applyi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate System
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the position of the points or other geometric elements on a manifold such as Euclidean space. The coordinates are not interchangeable; they are commonly distinguished by their position in an ordered tuple, or by a label, such as in "the ''x''-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and ''vice versa''; this is the basis of analytic geometry. Common coordinate systems Number line The simplest example of a coordinate system is the identification of points on a line with real numbers using the '' number line''. In this system, an arbitrary point ''O'' (the ''origin'') is chosen on a given line. The coordinate o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine. Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation. Trigonometry is known for its many identities. These trigonometric identities are commonly used for rewriting trigonometrical expressions with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation. History Sumerian astronomers studied angle me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangulation (surveying)
In surveying, triangulation is the process of determining the location of a point by measuring only angles to it from known points at either end of a fixed baseline by using trigonometry, rather than measuring distances to the point directly as in trilateration. The point can then be fixed as the third point of a triangle with one known side and two known angles. Triangulation can also refer to the accurate surveying of systems of very large triangles, called triangulation networks. This followed from the work of Willebrord Snellius, Willebrord Snell in 1615–17, who showed how a point could be located from the angles subtended from ''three'' known points, but measured at the new unknown point rather than the previously fixed points, a problem called Position resection and intersection, resectioning. Surveying error is minimized if a mesh of triangles at the largest appropriate scale is established first. Points inside the triangles can all then be accurately located with refere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
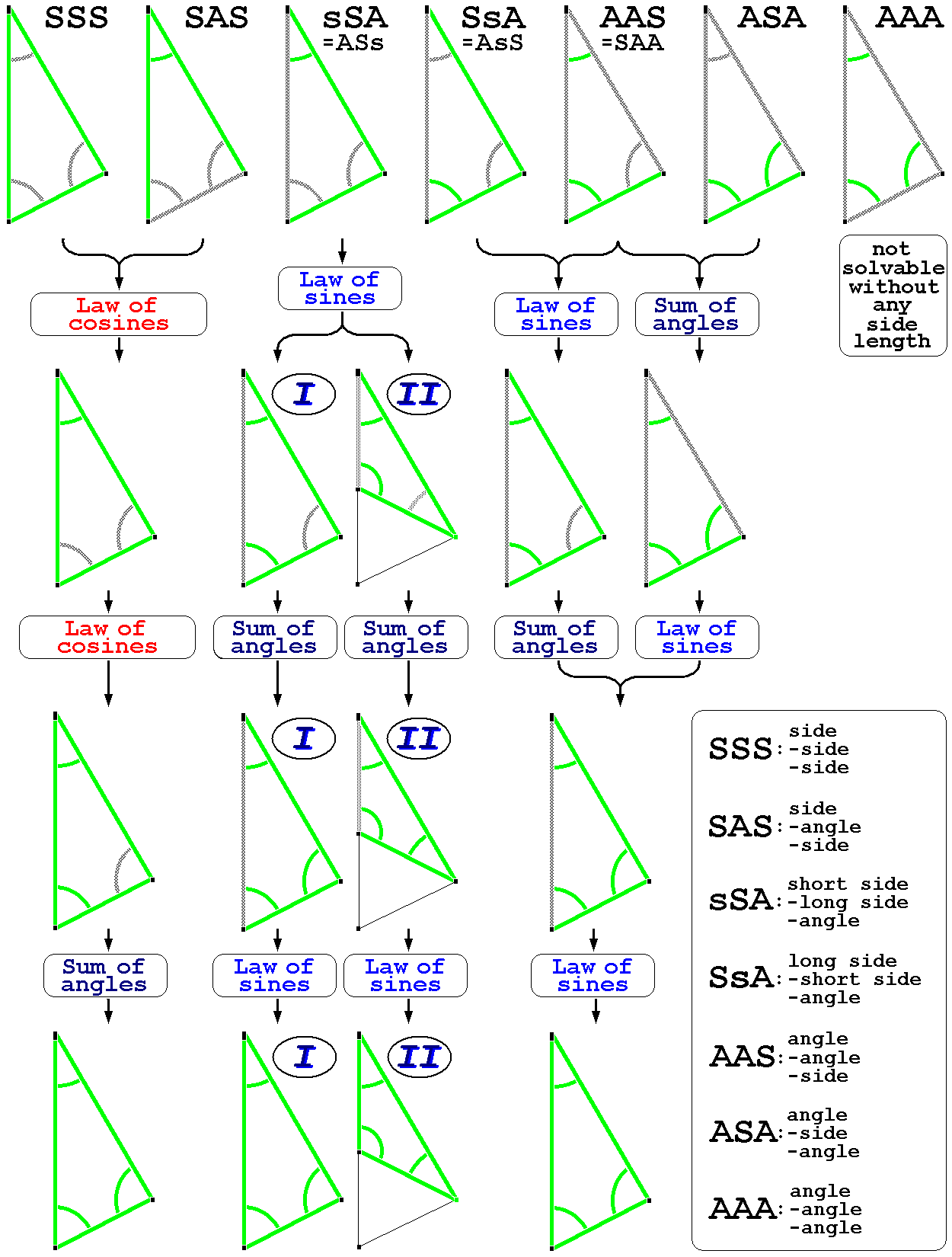
Solution Of Triangles
Solution of triangles () is the main trigonometric problem of finding the characteristics of a triangle (angles and lengths of sides), when some of these are known. The triangle can be located on a plane or on a sphere. Applications requiring triangle solutions include geodesy, astronomy, construction, and navigation. Solving plane triangles A general form triangle has six main characteristics (see picture): three linear (side lengths ) and three angular (). The classical plane trigonometry problem is to specify three of the six characteristics and determine the other three. A triangle can be uniquely determined in this sense when given any of the following: *Three sides (SSS) *Two sides and the included angle (SAS, side-angle-side) *Two sides and an angle not included between them (SSA), if the side length adjacent to the angle is shorter than the other side length. *A side and the two angles adjacent to it (ASA) *A side, the angle opposite to it and an angle adjacent to it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laurent Pothenot
{{Disambiguation ...
Laurent may refer to: *Laurent (name), a French masculine given name and a surname **Saint Laurence (aka: Saint ''Laurent''), the martyr Laurent **Pierre Alphonse Laurent, mathematician **Joseph Jean Pierre Laurent, amateur astronomer, discoverer of minor planet (51) Nemausa *Laurent, South Dakota, a proposed town for the Deaf to be named for Laurent Clerc See also *Laurent series, in mathematics, representation of a complex function ''f(z)'' as a power series which includes terms of negative degree, named for Pierre Alphonse Laurent *Saint-Laurent (other) *Laurence (name), feminine form of "Laurent" *Lawrence (other) Lawrence may refer to: Education Colleges and universities * Lawrence Technological University, a university in Southfield, Michigan, United States * Lawrence University, a liberal arts university in Appleton, Wisconsin, United States Preparator ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George Tyrrell McCaw
George may refer to: Names * George (given name) * George (surname) People * George (singer), American-Canadian singer George Nozuka, known by the mononym George * George Papagheorghe, also known as Jorge / GEØRGE * George, stage name of Giorgio Moroder * George, son of Andrew I of Hungary Places South Africa * George, South Africa, a city ** George Airport United States * George, Iowa, a city * George, Missouri, a ghost town * George, Washington, a city * George County, Mississippi * George Air Force Base, a former U.S. Air Force base located in California Computing * George (algebraic compiler) also known as 'Laning and Zierler system', an algebraic compiler by Laning and Zierler in 1952 * GEORGE (computer), early computer built by Argonne National Laboratory in 1957 * GEORGE (operating system), a range of operating systems (George 1–4) for the ICT 1900 range of computers in the 1960s * GEORGE (programming language), an autocode system invented by Charles Leonard Hamblin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yard
The yard (symbol: yd) is an English units, English unit of length in both the British imperial units, imperial and US United States customary units, customary systems of measurement equalling 3 foot (unit), feet or 36 inches. Since 1959 it has been by international yard and pound, international agreement standardized as exactly 0.9144 Metre, meter. A distance of 1,760 yards is equal to 1 mile. The theoretical survey foot, US survey yard is very slightly longer. Name The term, ''yard'' derives from the Old English , etc., which was used for branches, staves and measuring rods. It is first attested in the late 7th century Ine of Wessex#Laws, laws of Ine of Wessex, wherein the "yard of land" mentioned is the virgate, yardland, an old English unit of tax assessment equal to hide (unit), hide. Around the same time the Lindisfarne Gospels account of the messengers from John the Baptist in the Gospel of Matthew used it for a branch swayed by the wind. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclic Quadrilateral
In geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral (four-sided polygon) whose vertex (geometry), vertices all lie on a single circle, making the sides Chord (geometry), chords of the circle. This circle is called the ''circumcircle'' or ''circumscribed circle'', and the vertices are said to be ''concyclic''. The center of the circle and its radius are called the ''circumcenter'' and the ''circumradius'' respectively. Usually the quadrilateral is assumed to be convex polygon, convex, but there are also Crossed quadrilateral, crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case. The word cyclic is from the Ancient Greek (''kuklos''), which means "circle" or "wheel". All triangles have a circumcircle, but not all quadrilaterals do. An example of a quadrilateral that cannot be cyclic is a non-square rhombus. The section Cyclic quadrilateral#Characterizations, characterizations below states what necessar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inscribed Angle
In geometry, an inscribed angle is the angle formed in the interior of a circle when two chords intersect on the circle. It can also be defined as the angle subtended at a point on the circle by two given points on the circle. Equivalently, an inscribed angle is defined by two chords of the circle sharing an endpoint. The inscribed angle theorem relates the measure of an inscribed angle to that of the central angle intercepting the same arc. The inscribed angle theorem appears as Proposition 20 in Book 3 of Euclid's ''Elements''. Note that this theorem is not to be confused with the Angle bisector theorem, which also involves angle bisection (but of an angle of a triangle not inscribed in a circle). Theorem Statement The inscribed angle theorem states that an angle inscribed in a circle is half of the central angle that intercepts the same arc on the circle. Therefore, the angle does not change as its vertex is moved to different positions on the same arc of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4^2 = (-4)^2 = 16. Every nonnegative real number has a unique nonnegative square root, called the ''principal square root'' or simply ''the square root'' (with a definite article, see below), which is denoted by \sqrt, where the symbol "\sqrt" is called the '' radical sign'' or ''radix''. For example, to express the fact that the principal square root of 9 is 3, we write \sqrt = 3. The term (or number) whose square root is being considered is known as the ''radicand''. The radicand is the number or expression underneath the radical sign, in this case, 9. For non-negative , the principal square root can also be written in exponent notation, as x^. Every positive number has two square roots: \sqrt (which is positive) and -\sqrt (which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |