|
Simple Matching Coefficient
The simple matching coefficient (SMC) or Rand similarity coefficient is a statistic used for comparing the similarity and diversity of sample sets. Given two objects, A and B, each with ''n'' binary attributes, SMC is defined as: \begin \text & = \frac \\ pt& = \frac \end where *M_ is the total number of attributes where ''A'' and ''B'' both have a value of 0, *M_ is the total number of attributes where ''A'' and ''B'' both have a value of 1, *M_ is the total number of attributes where ''A'' has value 0 and ''B'' has value 1, and *M_ is the total number of attributes where ''A'' has value 1 and ''B'' has value 0. The simple matching distance (SMD), which measures dissimilarity between sample sets, is given by 1 - \text. SMC is linearly related to Hamann similarity: \text = (\text+1) / 2. Also, \text = 1 - D^2/n, where D^2 is the squared Euclidean distance between the two objects (binary vectors) and is the number of attributes. The SMC is very similar to the more popular J ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistic
A statistic (singular) or sample statistic is any quantity computed from values in a sample which is considered for a statistical purpose. Statistical purposes include estimating a population parameter, describing a sample, or evaluating a hypothesis. The average (or mean) of sample values is a statistic. The term statistic is used both for the function (e.g., a calculation method of the average) and for the value of the function on a given sample (e.g., the result of the average calculation). When a statistic is being used for a specific purpose, it may be referred to by a name indicating its purpose. When a statistic is used for estimating a population parameter, the statistic is called an '' estimator''. A population parameter is any characteristic of a population under study, but when it is not feasible to directly measure the value of a population parameter, statistical methods are used to infer the likely value of the parameter on the basis of a statistic computed from a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Similarity Measure
In statistics and related fields, a similarity measure or similarity function or similarity metric is a real-valued function that quantifies the similarity between two objects. Although no single definition of a similarity exists, usually such measures are in some sense the inverse of distance metrics: they take on large values for similar objects and either zero or a negative value for very dissimilar objects. Though, in more broad terms, a similarity function may also satisfy metric axioms. Cosine similarity is a commonly used similarity measure for real-valued vectors, used in (among other fields) information retrieval to score the similarity of documents in the vector space model. In machine learning, common kernel functions such as the RBF kernel can be viewed as similarity functions. Use of different similarity measure formulas Different types of similarity measures exist for various types of objects, depending on the objects being compared. For each type of object there ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sample (statistics)
In this statistics, quality assurance, and survey methodology, sampling is the selection of a subset or a statistical sample (termed sample for short) of individuals from within a population (statistics), statistical population to estimate characteristics of the whole population. The subset is meant to reflect the whole population, and statisticians attempt to collect samples that are representative of the population. Sampling has lower costs and faster data collection compared to recording data from the entire population (in many cases, collecting the whole population is impossible, like getting sizes of all stars in the universe), and thus, it can provide insights in cases where it is infeasible to measure an entire population. Each observation measures one or more properties (such as weight, location, colour or mass) of independent objects or individuals. In survey sampling, weights can be applied to the data to adjust for the sample design, particularly in stratified samplin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jaccard Index
The Jaccard index is a statistic used for gauging the similarity and diversity of sample sets. It is defined in general taking the ratio of two sizes (areas or volumes), the intersection size divided by the union size, also called intersection over union (IoU). It was developed by Grove Karl Gilbert in 1884 as his ratio of verification (v) and now is often called the critical success index in meteorology. It was later developed independently by Paul Jaccard, originally giving the French name (coefficient of community), and independently formulated again by Taffee Tadashi Tanimoto. Thus, it is also called Tanimoto index or Tanimoto coefficient in some fields. Overview The Jaccard index measures similarity between finite non-empty sample sets and is defined as the size of the intersection divided by the size of the union of the sample sets: : J(A, B) = \frac = \frac. Note that by design, 0 \le J(A, B) \le 1. If the sets A and B have no elements in common, their intersectio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dummy Variable (statistics)
In regression analysis, a dummy variable (also known as indicator variable or just dummy) is one that takes a binary value (0 or 1) to indicate the absence or presence of some categorical effect that may be expected to shift the outcome. For example, if we were studying the relationship between biological sex and income, we could use a dummy variable to represent the sex of each individual in the study. The variable could take on a value of 1 for males and 0 for females (or vice versa). In machine learning this is known as one-hot encoding. Dummy variables are commonly used in regression analysis to represent categorical variables that have more than two levels, such as education level or occupation. In this case, multiple dummy variables would be created to represent each level of the variable, and only one dummy variable would take on a value of 1 for each observation. Dummy variables are useful because they allow us to include categorical variables in our analysis, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a σ-algebra that satisfies Measure (mathematics), measure properties such as ''countable additivity''. The difference between a probability measure and the more general notion of measure (which includes concepts like area or volume) is that a probability measure must assign value 1 to the entire space. Intuitively, the additivity property says that the probability assigned to the union of two disjoint (mutually exclusive) events by the measure should be the sum of the probabilities of the events; for example, the value assigned to the outcome "1 or 2" in a throw of a dice should be the sum of the values assigned to the outcomes "1" and "2". Probability measures have applications in diverse fields, from physics to finance and biology. Definition The requirements for a set function \mu to be a probability measure on a σ-algebra are that: * \mu must return results in the unit interval ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
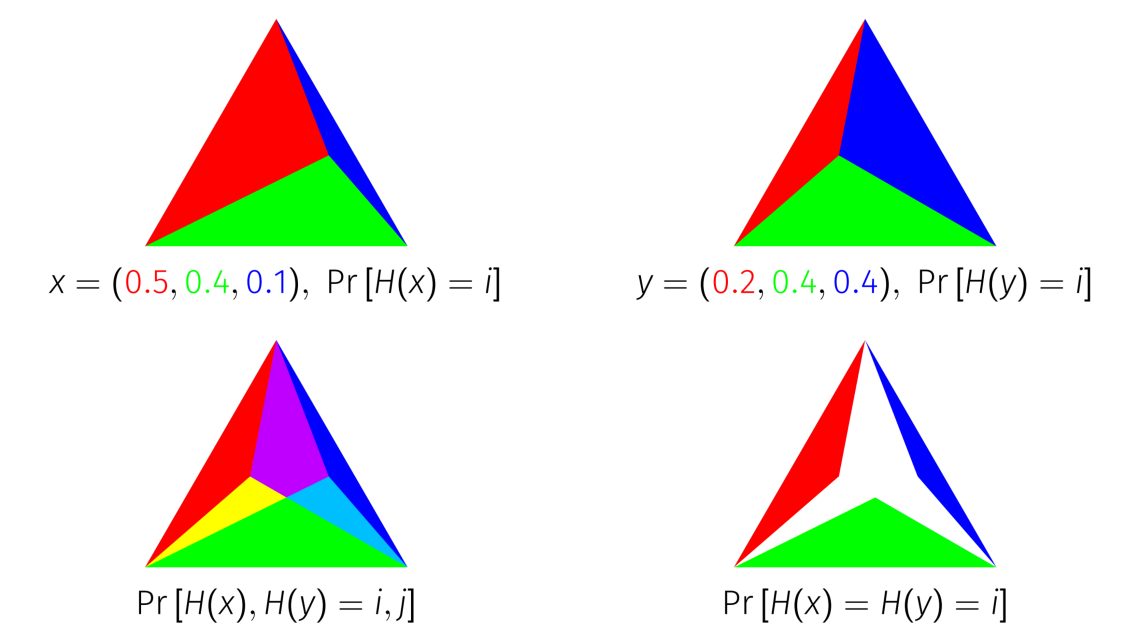
Rand Index
The Rand index or Rand measure (named after William M. Rand) in statistics, and in particular in data clustering, is a measure of the similarity between two data clusterings. A form of the Rand index may be defined that is adjusted for the chance grouping of elements, this is the adjusted Rand index. The Rand index is the accuracy of determining if a link belongs within a cluster or not. Rand index Definition Given a set of n elements S = \ and two partitions of S to compare, X = \, a partition of ''S'' into ''r'' subsets, and Y = \, a partition of ''S'' into ''s'' subsets, define the following: * a, the number of pairs of elements in S that are in the same subset in X and in the same subset in Y * b, the number of pairs of elements in S that are in different subsets in X and in different subsets in Y * c, the number of pairs of elements in S that are in the same subset in X and in different subsets in Y * d, the number of pairs of elements in S that are in different subsets in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Index Numbers
In economics, statistics, and finance, an index is a number that measures how a group of related data points—like prices, company performance, productivity, or employment—changes over time to track different aspects of economic health from various sources. Consumer-focused indices include the Consumer Price Index (CPI), which shows how retail prices for goods and services shift in a fixed area, aiding adjustments to salaries, bond interest rates, and tax thresholds for inflation. The cost-of-living index (COLI) compares living expenses over time or across places.Turvey, Ralph. (2004) Consumer Price Index Manual: Theory And Practice.' Page 11. Publisher: International Labour Organization. . ''The Economist''’s Big Mac Index uses a Big Mac’s cost to explore currency values and purchasing power. Market performance indices track trends like company value or employment. Stock market indices include the Dow Jones Industrial Average and S&P 500, which primarily cover U.S. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measure Theory
In mathematics, the concept of a measure is a generalization and formalization of geometrical measures (length, area, volume) and other common notions, such as magnitude (mathematics), magnitude, mass, and probability of events. These seemingly distinct concepts have many similarities and can often be treated together in a single mathematical context. Measures are foundational in probability theory, integral, integration theory, and can be generalized to assume signed measure, negative values, as with electrical charge. Far-reaching generalizations (such as spectral measures and projection-valued measures) of measure are widely used in quantum physics and physics in general. The intuition behind this concept dates back to Ancient Greece, when Archimedes tried to calculate the area of a circle. But it was not until the late 19th and early 20th centuries that measure theory became a branch of mathematics. The foundations of modern measure theory were laid in the works of Émile B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clustering Criteria
Clustering can refer to the following: In computing: *Computer cluster, the technique of linking many computers together to act like a single computer *Data cluster, an allocation of contiguous storage in databases and file systems *Cluster analysis, the statistical task of grouping a set of objects in such a way that objects in the same group are placed closer together (such as the k-means clustering) *In hash tables, the mapping of keys to nearby slots In economics: *Business cluster, a geographic concentration of interconnected businesses, suppliers, and associated institutions in a particular field In graph theory: *The formation of clusters of linked nodes in a network, measured by the clustering coefficient See also *Cluster (other) may refer to: Science and technology Astronomy * Cluster (spacecraft), constellation of four European Space Agency spacecraft * Cluster II (spacecraft), a European Space Agency mission to study the magnetosphere * Asteroid clu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
String Metrics
In mathematics and computer science, a string metric (also known as a string similarity metric or string distance function) is a metric that measures distance ("inverse similarity") between two text strings for approximate string matching or comparison and in fuzzy string searching. A requirement for a string ''metric'' (e.g. in contrast to string matching) is fulfillment of the triangle inequality. For example, the strings "Sam" and "Samuel" can be considered to be close. A string metric provides a number indicating an algorithm-specific indication of distance. The most widely known string metric is a rudimentary one called the Levenshtein distance (also known as edit distance). It operates between two input strings, returning a number equivalent to the number of substitutions and deletions needed in order to transform one input string into another. Simplistic string metrics such as Levenshtein distance have expanded to include phonetic, token, grammatical and character-based ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |