|
Simon Donaldson
Sir Simon Kirwan Donaldson (born 20 August 1957) is an English mathematician known for his work on the topology of smooth function, smooth (differentiable) four-dimensional manifolds, Donaldson–Thomas theory, and his contributions to Kähler geometry. He is currently a permanent member of the Simons Center for Geometry and Physics at Stony Brook University in New York, and a Professor in Pure Mathematics at Imperial College London. Biography Donaldson's father was an electrical engineer in the physiology department at the University of Cambridge, and his mother earned a science degree there. Donaldson gained a Bachelor of Arts, BA degree in mathematics from Pembroke College, Cambridge, in 1979, and in 1980 began postgraduate work at Worcester College, Oxford, at first under Nigel Hitchin and later under Michael Atiyah's supervision. Still a postgraduate student, Donaldson proved in 1982 a result that would establish his fame. He published the result in a paper "Self-dual ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
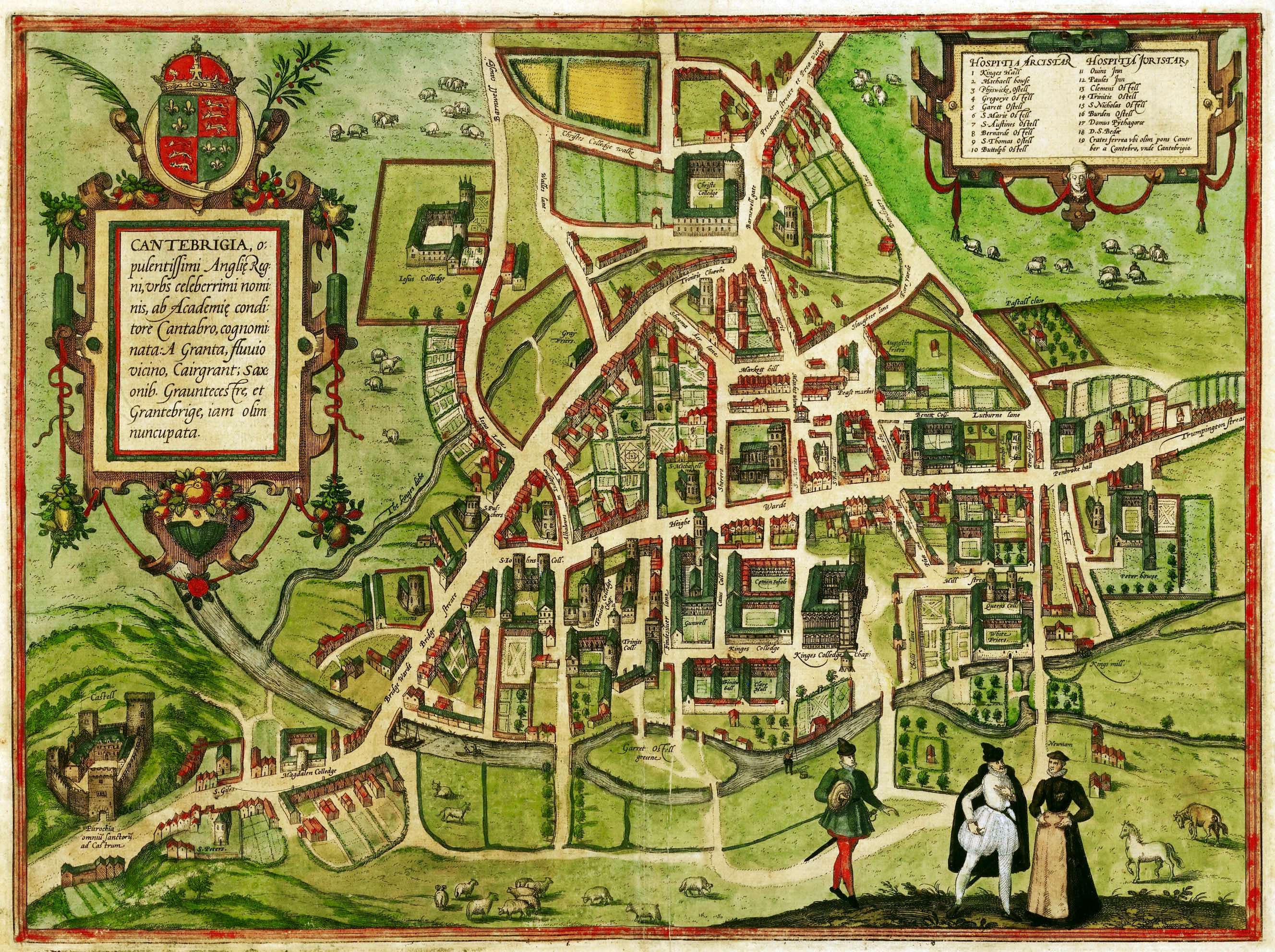
Cambridge
Cambridge ( ) is a List of cities in the United Kingdom, city and non-metropolitan district in the county of Cambridgeshire, England. It is the county town of Cambridgeshire and is located on the River Cam, north of London. As of the 2021 United Kingdom census, the population of the City of Cambridge was 145,700; the population of the wider built-up area (which extends outside the city council area) was 181,137. (2021 census) There is archaeological evidence of settlement in the area as early as the Bronze Age, and Cambridge became an important trading centre during the Roman Britain, Roman and Viking eras. The first Town charter#Municipal charters, town charters were granted in the 12th century, although modern city status was not officially conferred until 1951. The city is well known as the home of the University of Cambridge, which was founded in 1209 and consistently ranks among the best universities in the world. The buildings of the university include King's College Chap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paul Seidel
Paul Seidel (born 30 December 1970) is a Swiss-Italian mathematician specializing in homological mirror symmetry. He is a faculty member at the Massachusetts Institute of Technology. Career Seidel attended Heidelberg University, where he received his Diplom under supervision of Albrecht Dold in 1994. He then pursued his Ph.D. studies at the University of Oxford under supervision of Simon Donaldson (Thesis: ''Floer Homology and the Symplectic Isotopy Problem'') in 1998. He was a chargé de recherche at the CNRS from 1999 to 2002, a professor at Imperial College London from 2002 to 2003, a professor at the University of Chicago from 2003 to 2007, and then a professor at the Massachusetts Institute of Technology from 2007 onwards. Awards In 2000, Seidel was awarded the EMS Prize. In 2010, he was awarded the Oswald Veblen Prize in Geometry "for his fundamental contributions to symplectic geometry and, in particular, for his development of advanced algebraic methods for computatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fields Medal
The Fields Medal is a prize awarded to two, three, or four mathematicians under 40 years of age at the International Congress of Mathematicians, International Congress of the International Mathematical Union (IMU), a meeting that takes place every four years. The name of the award honours the Canadian mathematician John Charles Fields. The Fields Medal is regarded as one of the highest honors a mathematician can receive, and has been list of prizes known as the Nobel or the highest honors of a field, described as the Nobel Prize of Mathematics, although there are several major differences, including frequency of award, number of awards, age limits, monetary value, and award criteria. According to the annual Academic Excellence Survey by Academic Ranking of World Universities, ARWU, the Fields Medal is consistently regarded as the top award in the field of mathematics worldwide, and in another reputation survey conducted by IREG Observatory on Academic Ranking and Excellence, IR ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Junior Whitehead Prize
The Whitehead Prize is awarded yearly by the London Mathematical Society to multiple mathematicians working in the United Kingdom who are at an early stage of their career. The prize is named in memory of homotopy theory pioneer J. H. C. Whitehead. More specifically, people being considered for the award must be resident in the United Kingdom on 1 January of the award year or must have been educated in the United Kingdom. Also, the candidates must have less than 15 years of work at the postdoctorate level and must not have received any other prizes from the Society. Since the inception of the prize, no more than two could be awarded per year, but in 1999 this was increased to four "to allow for the award of prizes across the whole of mathematics, including applied mathematics, mathematical physics, and mathematical aspects of computer science". The Senior Whitehead Prize has similar residence requirements and rules concerning prior prizes, but is intended to recognize more expe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-stability Of Fano Varieties
In mathematics, and in particular algebraic geometry, K-stability is an algebro-geometric stability condition for projective algebraic varieties and complex manifolds. K-stability is of particular importance for the case of Fano varieties, where it is the correct stability condition to allow the formation of moduli spaces, and where it precisely characterises the existence of Kähler–Einstein metrics. The first attempt to define K-stability for Fano manifolds was made by Gang Tian in 1997, in response to a conjecture of Shing-Tung Yau from 1993 that there should exist a stability condition which characterises the existence of a Kähler–Einstein metric on a Fano manifold. It was defined in reference to the ''K-energy functional'' previously introduced by Toshiki Mabuchi. Tian's definition of K-stability was later replaced by a purely algebro-geometric refinement that was first formulated by Simon Donaldson in 2001. K-stability has become an important notion in the study an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-stability
In mathematics, and especially differential and algebraic geometry, K-stability is an algebro-geometric stability condition, for complex manifolds and complex algebraic varieties. The notion of K-stability was first introduced by Gang Tian and reformulated more algebraically later by Simon Donaldson. The definition was inspired by a comparison to geometric invariant theory (GIT) stability. In the special case of Fano varieties, K-stability precisely characterises the existence of Kähler–Einstein metrics. More generally, on any compact complex manifold, K-stability is conjectured to be equivalent to the existence of constant scalar curvature Kähler metrics (cscK metrics). History In 1954, Eugenio Calabi formulated a conjecture about the existence of Kähler metrics on compact Kähler manifolds, now known as the Calabi conjecture. One formulation of the conjecture is that a compact Kähler manifold X admits a unique Kähler–Einstein metric in the class c_1(X). In the par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kobayashi–Hitchin Correspondence
In differential geometry, algebraic geometry, and gauge theory, the Kobayashi–Hitchin correspondence (or Donaldson–Uhlenbeck–Yau theorem) relates stable vector bundles over a complex manifold to Einstein–Hermitian vector bundles. The correspondence is named after Shoshichi Kobayashi and Nigel Hitchin, who independently conjectured in the 1980s that the moduli spaces of stable vector bundles and Einstein–Hermitian vector bundles over a complex manifold were essentially the same. This was proven by Simon Donaldson for projective algebraic surfaces and later for projective algebraic manifolds, by Karen Uhlenbeck and Shing-Tung Yau for compact Kähler manifolds, and independently by Buchdahl for non-Kähler compact surfaces, and by Jun Li and Yau for arbitrary compact complex manifolds. The theorem can be considered a vast generalisation of the Narasimhan–Seshadri theorem concerned with the case of compact Riemann surfaces, and has been influential in the development ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Donaldson–Thomas Theory
In mathematics, specifically algebraic geometry Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; th ..., Donaldson–Thomas theory is the theory of Donaldson–Thomas invariants. Given a compact moduli space of sheaves on a Calabi–Yau threefold, its Donaldson–Thomas invariant is the virtual number of its points, i.e., the integral of the cohomology class 1 against the virtual fundamental class. The Donaldson–Thomas invariant is a holomorphic analogue of the Casson invariant. The invariants were introduced by . Donaldson–Thomas invariants have close connections to Gromov–Witten invariants of algebraic three-folds and the theory of stable pairs due to Rahul Pandharipande and Thomas. Donaldson–Thomas theory is physically motivated by certain BPS states that occur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Donaldson Theorem
In mathematics, and especially differential topology and gauge theory, Donaldson's theorem states that a definite intersection form of a compact, oriented, smooth manifold of dimension 4 is diagonalizable. If the intersection form is positive (negative) definite, it can be diagonalized to the identity matrix (negative identity matrix) over the . The original version of the theorem required the manifold to be simply connected, but it was later improved to apply to 4-manifolds with any fundamental group. History The theorem was proved by Simon Donaldson. This was a contribution cited for his Fields medal in 1986. Idea of proof Donaldson's proof utilizes the moduli space \mathcal_P of solutions to the anti-self-duality equations on a principal \operatorname(2)-bundle P over the four-manifold X. By the Atiyah–Singer index theorem, the dimension of the moduli space is given by :\dim \mathcal = 8k - 3(1-b_1(X) + b_+(X)), where k=c_2(P) is a Chern class, b_1(X) is the first Bett ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Donaldson Theory
In mathematics, and especially gauge theory, Donaldson theory is the study of the topology of smooth 4-manifolds using moduli spaces of anti-self-dual instantons. It was started by Simon Donaldson (1983) who proved Donaldson's theorem restricting the possible quadratic forms on the second cohomology group of a compact simply connected 4-manifold. Important consequences of this theorem include the existence of an exotic R4 and the failure of the smooth h-cobordism theorem in 4 dimensions. The results of Donaldson theory depend therefore on the manifold having a differential structure, and are largely false for topological 4-manifolds. Many of the theorems in Donaldson theory can now be proved more easily using Seiberg–Witten theory, though there are a number of open problems remaining in Donaldson theory, such as the Witten conjecture and the Atiyah–Floer conjecture. See also * Kronheimer–Mrowka basic class * Instanton An instanton (or pseudoparticle) is a notion appe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a Neighbourhood (mathematics), neighborhood that is homeomorphic to an open (topology), open subset of n-dimensional Euclidean space. One-dimensional manifolds include Line (geometry), lines and circles, but not Lemniscate, self-crossing curves such as a figure 8. Two-dimensional manifolds are also called Surface (topology), surfaces. Examples include the Plane (geometry), plane, the sphere, and the torus, and also the Klein bottle and real projective plane. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of systems of equations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Michael Thaddeus
Michael Thaddeus (born January 12, 1967) is an American mathematician and a professor of mathematics at Columbia University. He is best known for having been a whistleblower in exposing inaccurate data submitted by Columbia University to '' U.S. News & World Report'' (USNWR)'s Best Colleges Ranking to inflate the university's college ranking. Early life and education Thaddeus was born on January 12, 1967, in New York City, and grew up in Morningside Heights. His father, Patrick, and his mother, Janice, both held doctorates from Columbia. Thaddeus was educated at St. Hilda's & St. Hugh's School before enrolling at Hunter College High School in 1980, where he graduated in 1984. Thaddeus matriculated at Harvard University, where his sister was also a student, with the intent to study biology but switched to mathematics. He graduated in 1988 and was awarded a Rhodes Scholarship to study at St John's College, Oxford, where he earned his Doctor of Philosophy (DPhil). His dissert ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |