|
Siegmund Günther
Adam Wilhelm Siegmund Günther (6 February 1848 – 3 February 1923) was a German geographer, mathematician, historian of mathematics and natural scientist. Early life Born in 1848 to a German businessman, Günther would go on to attend several German universities including Erlangen, Heidelberg, Leipzig, Berlin, and Göttingen. Career In 1872 he began teaching at a school in Weissenburg, Bavaria. He completed his habilitation thesis on continued fractions entitled ''Darstellung der Näherungswerte der Kettenbrüche in independenter Form'' in 1873. The next year he began teaching at Munich Polytechnicum. In 1876, he began teaching at a university in Ansbach where he stayed for several years before moving to Munich and becoming a professor of geography until he retired; he served as the university's rector from 1911 to 1913. For some years, Günther was a member of the federal parliament, the Reichstag, and later the Bavarian parliament, representing liberal parties. His mathe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rector (academia)
A rector (Latin language, Latin for 'ruler') is a senior official in an educational institution, and can refer to an official in either a university or a secondary school. Outside the English-speaking world, the rector is often the most senior official in a university, while in the United States, the equivalent is often referred to as the President (education), president, and in the United Kingdom and Commonwealth of Nations, the equivalent is the Vice-chancellor (education), vice-chancellor. The term and office of a rector can be referred to as a rectorate. The title is used widely in universities in EuropeEuropean nations where the word ''rector'' or a cognate thereof (''rektor'', ''recteur'', etc.) is used in referring to university administrators include Albania, Austria, Benelux, the Benelux, Bosnia and Herzegovina, Bulgaria, Croatia, Cyprus, Czech Republic, Denmark, Estonia, Finland, Germany, Greece, Hungary, Iceland, Italy, Latvia, Malta, Moldova, North Macedonia, Poland, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ansbach
Ansbach ( , ; ) is a city in the Germany, German state of Bavaria. It is the capital of the Regierungsbezirk, administrative region of Mittelfranken, Middle Franconia. Ansbach is southwest of Nuremberg and north of Munich, on the river Fränkische Rezat, a tributary of the river Main (river), Main. In 2020, its population was 41,681. Developed in the 8th century as a Benedictine monastery, it became the seat of the House of Hohenzollern, Hohenzollern family in 1331. In 1460, the Margraves of Fürst und Markgraf von Ansbach, Brandenburg-Ansbach lived here. The city has a castle known as Markgrafenschloß, Margrafen–Schloss, built between 1704 and 1738. It was not badly damaged during the World Wars and hence retains its original historical baroque sheen. Ansbach is now home to a US military base and to the Ansbach University of Applied Sciences. The city has connections via autobahn Bundesautobahn 6, A6 and highways Bundesstraße 13, B13 and Bundesstraße 14, B14. Ansbach st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Members Of The Bavarian Chamber Of Deputies
Member may refer to: * Military jury, referred to as "Members" in military jargon * Element (mathematics), an object that belongs to a mathematical set * In object-oriented programming, a member of a class ** Field (computer science), entries in a database ** Member variable, a variable that is associated with a specific object * Limb (anatomy), an appendage of the human or animal body ** Euphemism for penis * Structural component of a truss, connected by nodes * User (computing), a person making use of a computing service, especially on the Internet * Member (geology), a component of a geological formation * Member of parliament * The Members, a British punk rock band * Meronymy, a semantic relationship in linguistics * Church membership, belonging to a local Christian congregation, a Christian denomination and the universal Church * Member, a participant in a club or learned society A learned society ( ; also scholarly, intellectual, or academic society) is an organizatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Presidents Of The Technical University Of Munich
President most commonly refers to: *President (corporate title) *President (education), a leader of a college or university *President (government title) President may also refer to: Arts and entertainment Film and television *'' Præsidenten'', a 1919 Danish silent film directed by Carl Theodor Dreyer * ''The President'' (1928 film), a German silent drama * ''President'' (1937 film), an Indian film * ''The President'' (1961 film) * ''The Presidents'' (film), a 2005 documentary * ''The President'' (2014 film) * ''The President'' (South Korean TV series), a 2010 South Korean television series * ''The President'' (Palestinian TV series), a 2013 Palestinian reality television show *''The President Show'', a 2017 Comedy Central political satirical parody sitcom * ''Presidents'' (film), a 2021 French film Music * The Presidents (American soul band) *The Presidents of the United States of America (band) or the Presidents, an American alternative rock group *"The President", a song ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Academic Staff Of The Technical University Of Munich
An academy (Attic Greek: Ἀκαδήμεια; Koine Greek Ἀκαδημία) is an institution of tertiary education. The name traces back to Plato's school of philosophy, founded approximately 386 BC at Akademia, a sanctuary of Athena, the goddess of wisdom and skill, north of Athens, Greece. The Royal Spanish Academy defines academy as scientific, literary or artistic society established with public authority and as a teaching establishment, public or private, of a professional, artistic, technical or simply practical nature. Etymology The word comes from the ''Academy'' in ancient Greece, which derives from the Athenian hero, ''Akademos''. Outside the city walls of Athens, the gymnasium was made famous by Plato as a center of learning. The sacred space, dedicated to the goddess of wisdom, Athena, had formerly been an olive grove, hence the expression "the groves of Academe". In these gardens, the philosopher Plato conversed with followers. Plato developed his sessions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
19th-century German Mathematicians
The 19th century began on 1 January 1801 (represented by the Roman numerals MDCCCI), and ended on 31 December 1900 (MCM). It was the 9th century of the 2nd millennium. It was characterized by vast social upheaval. Slavery was abolished in much of Europe and the Americas. The First Industrial Revolution, though it began in the late 18th century, expanded beyond its British homeland for the first time during the 19th century, particularly remaking the economies and societies of the Low Countries, France, the Rhineland, Northern Italy, and the Northeastern United States. A few decades later, the Second Industrial Revolution led to ever more massive urbanization and much higher levels of productivity, profit, and prosperity, a pattern that continued into the 20th century. The Catholic Church, in response to the growing influence and power of modernism, secularism and materialism, formed the First Vatican Council in the late 19th century to deal with such problems and confirm ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1923 Deaths
In Greece, this year contained only 352 days as 13 days was skipped to achieve the calendrical switch from Julian to Gregorian Calendar. It happened there that Wednesday, 15 February ''(Julian Calendar)'' was followed by Thursday, 1 March ''(Gregorian Calendar).'' Events January–February * January 9, January 5 – Lithuania begins the Klaipėda Revolt to annex the Klaipėda Region (Memel Territory). * January 11 – Despite strong British protests, troops from France and Belgium Occupation of the Ruhr, occupy the Ruhr area, to force Germany to make reparation payments. * January 17 (or 9) – First flight of the first rotorcraft, Juan de la Cierva's Cierva C.4 autogyro, in Spain. (It is first demonstrated to the military on January 31.) * February 5 – Australian cricketer Bill Ponsford makes 429 runs to break the world record for the highest first-class cricket score for the first time in his third match at this level, at Melbourne Cricket Ground, giving the Victor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1848 Births
1848 is historically famous for the wave of revolutions, a series of widespread struggles for more liberal governments, which broke out from Brazil to Hungary; although most failed in their immediate aims, they significantly altered the political and philosophical landscape and had major ramifications throughout the rest of the century. Ereignisblatt aus den revolutionären Märztagen 18.-19. März 1848 mit einer Barrikadenszene aus der Breiten Strasse, Berlin 01.jpg, Cheering revolutionaries in Berlin, on March 19, 1848, with the new flag of Germany Lar9 philippo 001z.jpg, French Revolution of 1848: Republican riots force King Louis-Philippe to abdicate Zeitgenössige Lithografie der Nationalversammlung in der Paulskirche.jpg, German National Assembly's meeting in St. Paul's Church Pákozdi csata.jpg, Battle of Pákozd in the Hungarian Revolution of 1848 Events January–March * January 3 – Joseph Jenkins Roberts is sworn in as the first president of the inde ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Andreas Daum
Andreas W. Daum is a German-American historian who specializes in modern German and transatlantic history, as well as the history of knowledge and global exploration. Daum received his Ph.D. summa cum laude in 1995 from the Ludwig Maximilian University of Munich, where he taught for six years as an assistant professor. In 1996, he joined the German Historical Institute Washington DC as a research fellow. From 2001 to 2002, Daum was a John F. Kennedy Memorial Fellow at the Center for European Studies at Harvard University. Since 2003, he has been a professor of European history at the State University of New York (SUNY) at Buffalo. He also served as an associate dean for undergraduate education in the provost's office. In 2010–11, he was a visiting scholar at the BMW Center for German and European Studies at Georgetown University. He is best known as a biographer of Alexander von Humboldt and for his studies on popular science, emigrants from Nazi Germany, and the United State ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
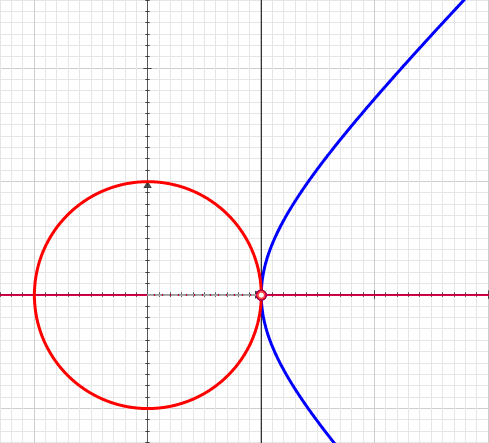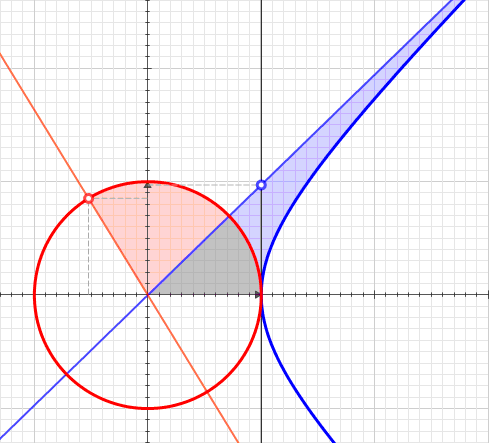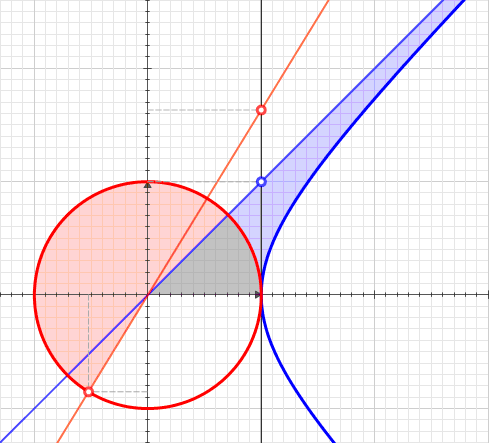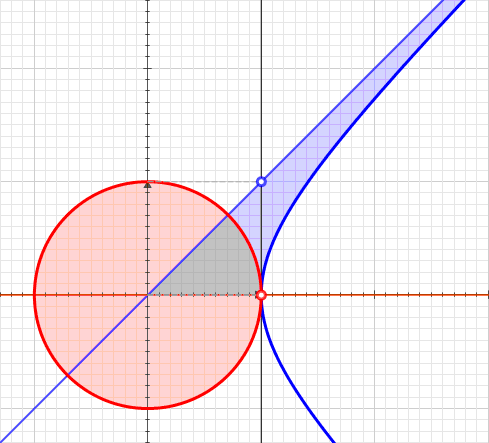
Hyperbolic Angle
In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of ''xy'' = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrizes the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation. The hyperbola ''xy'' = 1 is rectangular with semi-major axis \sqrt 2, analogous to the circular angle equaling the area of a circular sector in a circle with radius \sqrt 2. Hyperbolic angle is used as the independent variable for the hyperbolic functions sinh, cosh, and tanh, because these functions may be premised on hyperbolic analogies to the corresponding circular (trigonometric) functions by regarding a hyperbolic angle as defining a hyperbolic triangle. The parameter thus becomes one of the most useful in the calculus of real variables. Definition Consider the rectangular hyperbola \textstyle\, and (by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if the base is implicit, simply . Parentheses are sometimes added for clarity, giving , , or . This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity. The natural logarithm of is the exponentiation, power to which would have to be raised to equal . For example, is , because . The natural logarithm of itself, , is , because , while the natural logarithm of is , since . The natural logarithm can be defined for any positive real number as the Integral, area under the curve from to (with the area being negative when ). The simplicity of this definition, which is matched in many other formulas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |