|
Shear Mapping
In plane geometry, a shear mapping is an affine transformation that displaces each point in a fixed direction by an amount proportional to its signed distance function, signed distance from a given straight line, line parallel (geometry), parallel to that direction. This type of mapping is also called shear transformation, transvection, or just shearing. The transformations can be applied with a shear matrix or transvection, an elementary matrix that represents the Elementary row operations#Row-addition transformations, addition of a multiple of one row or column to another. Such a matrix (mathematics), matrix may be derived by taking the identity matrix and replacing one of the zero elements with a non-zero value. An example is the linear map that takes any point with Cartesian coordinates, coordinates (x,y) to the point (x + 2y,y). In this case, the displacement is horizontal by a factor of 2 where the fixed line is the -axis, and the signed distance is the -coordinate. Not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelogram
In Euclidean geometry, a parallelogram is a simple polygon, simple (non-list of self-intersecting polygons, self-intersecting) quadrilateral with two pairs of Parallel (geometry), parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence (geometry), congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations. By comparison, a quadrilateral with at least one pair of parallel sides is a trapezoid in American English or a trapezium in British English. The three-dimensional counterpart of a parallelogram is a parallelepiped. The word "parallelogram" comes from the Greek παραλληλό-γραμμον, ''parallēló-grammon'', which means "a shape of parallel lines". Special cases *Rectangle – A par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SVG SkewX
Scalable Vector Graphics (SVG) is an XML-based vector graphics format for defining two-dimensional graphics, having support for interactivity and animation. The SVG specification is an open standard developed by the World Wide Web Consortium since 1999. SVG images are defined in a vector graphics format and stored in XML text files. SVG images can thus be scaled in size without loss of quality, and SVG files can be searched, indexed, scripted, and compressed. The XML text files can be created and edited with text editors or vector graphics editors, and are rendered by most web browsers. If used for images, SVG can host scripts or CSS, potentially leading to cross-site scripting attacks or other security vulnerabilities. History SVG has been in development within the World Wide Web Consortium (W3C) since 1999 after six competing proposals for vector graphics languages had been submitted to the consortium during 1998 (see below). The early SVG Working Group decided not to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measure (mathematics)
In mathematics, the concept of a measure is a generalization and formalization of geometrical measures (length, area, volume) and other common notions, such as magnitude, mass, and probability of events. These seemingly distinct concepts have many similarities and can often be treated together in a single mathematical context. Measures are foundational in probability theory, integration theory, and can be generalized to assume negative values, as with electrical charge. Far-reaching generalizations (such as spectral measures and projection-valued measures) of measure are widely used in quantum physics and physics in general. The intuition behind this concept dates back to Ancient Greece, when Archimedes tried to calculate the area of a circle. But it was not until the late 19th and early 20th centuries that measure theory became a branch of mathematics. The foundations of modern measure theory were laid in the works of Émile Borel, Henri Lebesgue, Nikolai Luzin, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Transformation
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism. If a linear map is a bijection then it is called a . In the case where V = W, a linear map is called a linear endomorphism. Sometimes the term refers to this case, but the term "linear operator" can have different meanings for different conventions: for example, it can be used to emphasize that V and W are real vector spaces (not necessarily with V = W), or it can be used to emphasize that V is a function space, which is a common convention in functional analysis. Sometimes the term ''linear function'' has the same meaning as ''linear map' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is one less than that of the ambient space. Two lower-dimensional examples of hyperplanes are one-dimensional lines in a plane and zero-dimensional points on a line. Most commonly, the ambient space is -dimensional Euclidean space, in which case the hyperplanes are the -dimensional "flats", each of which separates the space into two half spaces. A reflection across a hyperplane is a kind of motion ( geometric transformation preserving distance between points), and the group of all motions is generated by the reflections. A convex polytope is the intersection of half-spaces. In non-Euclidean geometry, the ambient space might be the -dimensional sphere or hyperbolic space, or more generally a pseudo-Riemannian space form, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Geometry
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry. Analytic geometry is used in physics and engineering, and also in aviation, rocketry, space science, and spaceflight. It is the foundation of most modern fields of geometry, including algebraic, differential, discrete and computational geometry. Usually the Cartesian coordinate system is applied to manipulate equations for planes, straight lines, and circles, often in two and sometimes three dimensions. Geometrically, one studies the Euclidean plane (two dimensions) and Euclidean space. As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometric shapes in a numerical way and extracting numerical information from shapes' numerical definitions and representations. That the algebra of the real numbers can be employed to yield r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
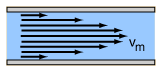
Laminar Flow
Laminar flow () is the property of fluid particles in fluid dynamics to follow smooth paths in layers, with each layer moving smoothly past the adjacent layers with little or no mixing. At low velocities, the fluid tends to flow without lateral mixing, and adjacent layers slide past one another smoothly. There are no cross-currents perpendicular to the direction of flow, nor eddies or swirls of fluids. In laminar flow, the motion of the particles of the fluid is very orderly with particles close to a solid surface moving in straight lines parallel to that surface. Laminar flow is a flow regime characterized by high momentum diffusion and low momentum convection. When a fluid is flowing through a closed channel such as a pipe or between two flat plates, either of two types of flow may occur depending on the velocity and viscosity of the fluid: laminar flow or turbulent flow. Laminar flow occurs at lower velocities, below a threshold at which the flow becomes turbulent. The thresh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-dimensional Geometry
Solid geometry or stereometry is the geometry of three-dimensional Euclidean space (3D space). A solid figure is the region of 3D space bounded by a two-dimensional closed surface; for example, a solid ball consists of a sphere and its interior. Solid geometry deals with the measurements of volumes of various solids, including pyramids, prisms (and other polyhedrons), cubes, cylinders, cones (and truncated cones). History The Pythagoreans dealt with the regular solids, but the pyramid, prism, cone and cylinder were not studied until the Platonists. Eudoxus established their measurement, proving the pyramid and cone to have one-third the volume of a prism and cylinder on the same base and of the same height. He was probably also the discoverer of a proof that the volume enclosed by a sphere is proportional to the cube of its radius.Paraphrased and taken in part from the ''1911 Encyclopædia Britannica''. Topics Basic topics in solid geometry and stereometry include: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latin Alphabet
The Latin alphabet, also known as the Roman alphabet, is the collection of letters originally used by the Ancient Rome, ancient Romans to write the Latin language. Largely unaltered except several letters splitting—i.e. from , and from —additions such as , and extensions such as letters with diacritics, it forms the Latin script that is used to write most languages of modern Languages of Europe, Europe, languages of Africa, Africa, languages of the Americas, the Americas, and Languages of Oceania, Oceania. Its basic modern inventory is standardized as the ISO basic Latin alphabet. Etymology The term ''Latin alphabet'' may refer to either the alphabet used to write Latin (as described in this article) or other alphabets based on the Latin script, which is the basic set of letters common to the various alphabets descended from the classical Latin alphabet, such as the English alphabet. These Latin-script alphabets may discard letters, like the Rotokas alphabet, or add new ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Italic Font
In typography, italic type is a cursive font based on a stylised form of calligraphic handwriting. Along with blackletter and roman type, it served as one of the major typefaces in the history of Western typography. Owing to the influence from calligraphy, italics normally slant slightly to the right, ''like so''. Different glyph shapes from roman type are usually usedanother influence from calligraphyand upper-case letters may have swashes, flourishes inspired by ornate calligraphy. Historically, italics were a distinct style of type used entirely separately from roman type, but they have come to be used in conjunction—most fonts now come with a roman type and an oblique version (generally called "italic" though often not true italics). In this usage, italics are a way to emphasise key points in a printed text, to identify many types of creative works, to cite foreign words or phrases, or, when quoting a speaker, a way to show which words they stressed. One manual o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Collinear
In geometry, collinearity of a set of Point (geometry), points is the property of their lying on a single Line (geometry), line. A set of points with this property is said to be collinear (sometimes spelled as colinear). In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row". Points on a line In any geometry, the set of points on a line are said to be collinear. In Euclidean geometry this relation is intuitively visualized by points lying in a row on a "straight line". However, in most geometries (including Euclidean) a Line (geometry), line is typically a Primitive notion, primitive (undefined) object type, so such visualizations will not necessarily be appropriate. A Mathematical model, model for the geometry offers an interpretation of how the points, lines and other object types relate to one another and a notion such as collinearity must be interpreted within the context of that model. For instance, in spherical g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |