|
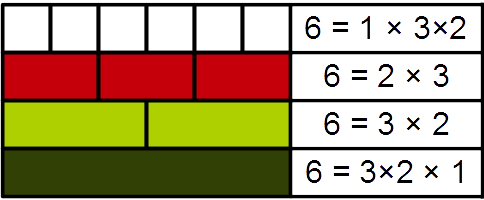
Semiprime
In mathematics, a semiprime is a natural number that is the product of exactly two prime numbers. The two primes in the product may equal each other, so the semiprimes include the squares of prime numbers. Because there are infinitely many prime numbers, there are also infinitely many semiprimes. Semiprimes are also called biprimes, since they include two primes, or second numbers, by analogy with how "prime" means "first". Alternatively non-prime semiprimes are called almost-prime numbers, specifically the "2-almost-prime" biprime and "3-almost-prime" triprime Examples and variations The semiprimes less than 100 are: Semiprimes that are not square numbers are called discrete, distinct, or squarefree semiprimes: The semiprimes are the case k=2 of the k- almost primes, numbers with exactly k prime factors. However some sources use "semiprime" to refer to a larger set of numbers, the numbers with at most two prime factors (including unit (1), primes, and semiprimes). These are: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Factorization
In mathematics, integer factorization is the decomposition of a positive integer into a product of integers. Every positive integer greater than 1 is either the product of two or more integer factors greater than 1, in which case it is a composite number, or it is not, in which case it is a prime number. For example, is a composite number because , but is a prime number because it cannot be decomposed in this way. If one of the factors is composite, it can in turn be written as a product of smaller factors, for example . Continuing this process until every factor is prime is called prime factorization; the result is always unique up to the order of the factors by the prime factorization theorem. To factorize a small integer using mental or pen-and-paper arithmetic, the simplest method is trial division: checking if the number is divisible by prime numbers , , , and so on, up to the square root of . For larger numbers, especially when using a computer, various more sophis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
RSA Factoring Challenge
The RSA Factoring Challenge was a challenge put forward by RSA Laboratories on March 18, 1991 to encourage research into computational number theory and the practical difficulty of factoring large integers and cracking RSA keys used in cryptography. They published a list of semiprimes (numbers with exactly two prime factors) known as the RSA numbers, with a cash prize for the successful factorization of some of them. The smallest of them, a 100-decimal digit number called RSA-100 was factored by April 1, 1991. Many of the bigger numbers have still not been factored and are expected to remain unfactored for quite some time, however advances in quantum computers make this prediction uncertain due to Shor's algorithm. In 2001, RSA Laboratories expanded the factoring challenge and offered prizes ranging from $10,000 to $200,000 for factoring numbers from 576 bits up to 2048 bits. The RSA Factoring Challenges ended in 2007. RSA Laboratories stated: "Now that the industry has a cons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Numbers
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number , called trial division, tests whether is a multiple of any integer between 2 and . Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always produ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorization, factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow primality test, method of checking the primality of a given number , called trial division, tests whether is a multiple of any integer between 2 and . Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parity Problem (sieve Theory)
In number theory, the parity problem refers to a limitation in sieve theory that prevents sieves from giving good estimates in many kinds of prime-counting problems. The problem was identified and named by Atle Selberg in 1949. Beginning around 1996, John Friedlander and Henryk Iwaniec developed some parity-sensitive sieves that make the parity problem less of an obstacle. Statement Terence Tao gave this "rough" statement of the problem: This problem is significant because it may explain why it is difficult for sieves to "detect primes," in other words to give a non-trivial lower bound for the number of primes with some property. For example, in a sense Chen's theorem is very close to a solution of the twin prime conjecture, since it says that there are infinitely many primes ''p'' such that ''p'' + 2 is either prime or the product of two primes (semiprime). The parity problem suggests that, because the case of interest has an odd number of prime factors (namely 1), it won't be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Almost Prime
In number theory, a natural number is called -almost prime if it has prime factors. More formally, a number is -almost prime if and only if , where is the total number of primes in the prime factorization of (can be also seen as the sum of all the primes' exponents): :\Omega(n) := \sum a_i \qquad\mbox\qquad n = \prod p_i^. A natural number is thus prime if and only if it is 1-almost prime, and semiprime if and only if it is 2-almost prime. The set of -almost primes is usually denoted by . The smallest -almost prime is . The first few -almost primes are: : The number of positive integers less than or equal to with exactly prime divisors (not necessarily distinct) is asymptotic to: : \pi_k(n) \sim \left( \frac \right) \frac, a result of Landau Landau (), officially Landau in der Pfalz (, ), is an autonomous (''kreisfrei'') town surrounded by the Südliche Weinstraße ("Southern Wine Route") district of southern Rhineland-Palatinate, Germany. It is a university town ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Composite Number
A composite number is a positive integer that can be formed by multiplying two smaller positive integers. Accordingly it is a positive integer that has at least one divisor other than 1 and itself. Every positive integer is composite, prime number, prime, or the Unit (ring theory), unit 1, so the composite numbers are exactly the numbers that are not prime and not a unit. E.g., the integer 14 is a composite number because it is the product of the two smaller integers 2 × 7 but the integers 2 and 3 are not because each can only be divided by one and itself. The composite numbers up to 150 are: :4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108, 110, 111, 112, 114, 115, 116, 117, 118, 119, 120, 121, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chen's Theorem
In number theory, Chen's theorem states that every sufficiently large parity (mathematics), even number can be written as the sum of either two prime number, primes, or a prime and a semiprime (the product of two primes). It is a weakened form of Goldbach's conjecture, which states that every even number is the sum of two primes. History The theorem was first stated by China, Chinese mathematician Chen Jingrun in 1966, with further details of the mathematical proof, proof in 1973. His original proof was much simplified by P. M. Ross in 1975. Chen's theorem is a significant step towards Goldbach's conjecture, and a celebrated application of sieve theory, sieve methods. Chen's theorem represents the strengthening of a previous result due to Alfréd Rényi, who in 1947 had shown there exists a finite ''K'' such that any even number can be written as the sum of a prime number and the product of at most ''K'' primes. Variations Chen's 1973 paper stated two results with nearly i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arecibo Message
The Arecibo message is an interstellar radio message carrying basic information about humanity and Earth that was sent to the globular cluster Messier 13 in 1974. It was meant as a demonstration of human technological achievement, rather than a real attempt to enter into a conversation with extraterrestrials. The message was broadcast into space a single time via frequency modulated radio waves at a ceremony to mark the remodeling of the Arecibo Telescope in Puerto Rico on 16 November 1974. The message was aimed at the current location of M13, about 25,000 light years from Earth, because M13 was a large and relatively close collection of stars that was available in the sky at the time and place of the ceremony. When correctly translated into graphics, characters, and spaces, the 1,679 bits of data contained within the message form the image shown here. Description The content of the Arecibo message was designed by a group of Cornell University and Arecibo scientists: Frank ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cryptography
Cryptography, or cryptology (from "hidden, secret"; and ''graphein'', "to write", or ''-logy, -logia'', "study", respectively), is the practice and study of techniques for secure communication in the presence of Adversary (cryptography), adversarial behavior. More generally, cryptography is about constructing and analyzing Communication protocol, protocols that prevent third parties or the public from reading private messages. Modern cryptography exists at the intersection of the disciplines of mathematics, computer science, information security, electrical engineering, digital signal processing, physics, and others. Core concepts related to information security (confidentiality, data confidentiality, data integrity, authentication, and non-repudiation) are also central to cryptography. Practical applications of cryptography include electronic commerce, Smart card#EMV, chip-based payment cards, digital currencies, password, computer passwords, and military communications. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blum Blum Shub
Blum Blum Shub (B.B.S.) is a pseudorandom number generator proposed in 1986 by Lenore Blum, Manuel Blum and Michael Shub that is derived from Michael O. Rabin's one-way function. __TOC__ Blum Blum Shub takes the form :x_ = x_n^2 \bmod M, where ''M'' = ''pq'' is the product of two large primes ''p'' and ''q''. At each step of the algorithm, some output is derived from ''x''''n''+1; the output is commonly either the bit parity of ''x''''n''+1 or one or more of the least significant bits of ''x''''n''+1. The seed ''x''0 should be an integer that is co-prime to ''M'' (i.e. ''p'' and ''q'' are not factors of ''x''0) and not 1 or 0. The two primes, ''p'' and ''q'', should both be congruent to 3 (mod 4) (this guarantees that each quadratic residue has one square root which is also a quadratic residue), and should be safe primes with a small gcd((''p-3'')''/2'', (''q-3'')''/2'') (this makes the cycle length large). An interesting characteristic of the Blum Blum Shub generator is t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Sequences
In mathematics, an integer sequence is a sequence (i.e., an ordered list) of integers. An integer sequence may be specified ''explicitly'' by giving a formula for its ''n''th term, or ''implicitly'' by giving a relationship between its terms. For example, the sequence 0, 1, 1, 2, 3, 5, 8, 13, ... (the Fibonacci sequence) is formed by starting with 0 and 1 and then adding any two consecutive terms to obtain the next one: an implicit description . The sequence 0, 3, 8, 15, ... is formed according to the formula ''n''2 − 1 for the ''n''th term: an explicit definition. Alternatively, an integer sequence may be defined by a property which members of the sequence possess and other integers do not possess. For example, we can determine whether a given integer is a perfect number, , even though we do not have a formula for the ''n''th perfect number. Computable and definable sequences An integer sequence is computable if there exists an algorithm that, given '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |