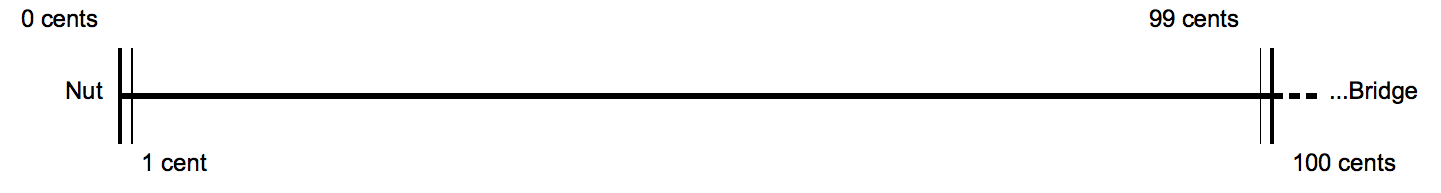|
Semicomma
The semicomma,Haluska, Jan (2003). ''The Mathematical Theory of Tone Systems'', p.xxix. . also Fokker's comma (after 31-TET pioneer Adriaan Fokker), is type of small musical interval, or comma, in microtonal music equivalent to 2109375:2097152, or . This is a ratio of approximately 1:1.0058283805847168, or about 10.06 cents (). It is derived from the difference in pitch between three 75:64 just augmented seconds () and one 8:5 just minor sixth () begun on the same root ((3 × 274.58) − (1 × 813.69) = 823.74 − 813.69 = 10.05 cents). It can also be viewed as the amount by which three tritaves exceed seven minor sixths. See also * Septimal kleisma *Septimal semicomma In music, the septimal semicomma, a seven-limit semicomma, is the ratio 126/125 and is equal to approximately 13.79 cents (). It is also called the ''small septimal comma''Haluska, Jan (2003). ''The Mathematical Theory of Tone Systems'', p.xxvi. . ... References {{Intervals, state=expanded 5-limit tuning and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Comma (music)
In music theory, a comma is a very small interval, the difference resulting from tuning one note two different ways. Strictly speaking, there are only two kinds of comma, the syntonic comma, "the difference between a just major 3rd and four just perfect 5ths less two octaves", and the Pythagorean comma, "the difference between twelve 5ths and seven octaves". The word ''comma'' used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F tuned using the D-based Pythagorean tuning system, and another F tuned using the D-based quarter-comma meantone tuning system. Intervals separated by the ratio 81:80 are considered the same note because the 12-note Western chromatic scale does not distinguish Pythagorean intervals from 5-limit intervals in its notation. Other intervals are considered commas because of the enharmonic equivalences of a tuning system. For example, in 53TET, B and A are both approximated by the same ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals, or to compare the sizes of comparable intervals in different tuning systems, and in fact the interval of one cent is too small to be perceived between successive notes. Cents, as described by Alexander John Ellis, follow a tradition of measuring intervals by logarithms that began with Juan Caramuel y Lobkowitz in the 17th century. Ellis chose to base his measures on the hundredth part of a semitone, , at Robert Holford Macdowell Bosanquet's suggestion. He made extensive measurements of musical instruments from around the world, using cents extensively to report and compare the scales employed, and further described and employed the system in his 1875 edition of Hermann von Helmholtz's ''On the Sensations of Tone''. It has become the standard method of representi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
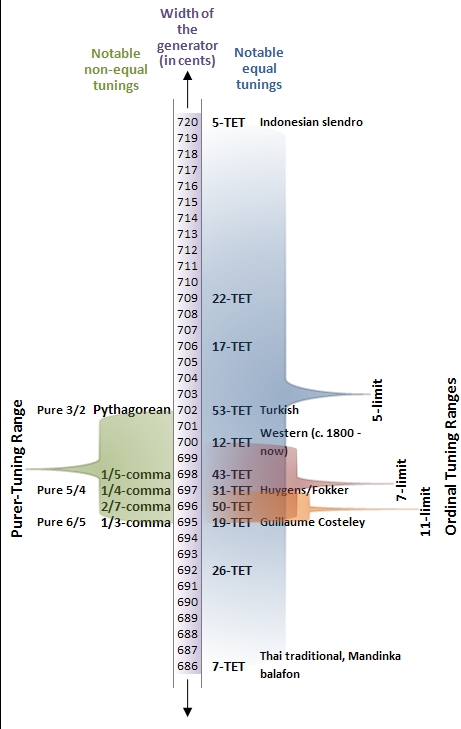
31-TET
In music, 31 equal temperament, 31-ET, which can also be abbreviated 31-TET (31 tone ET) or 31-EDO (equal division of the octave), also known as tricesimoprimal, is the tempered scale derived by dividing the octave into 31 equal-sized steps (equal frequency ratios). Each step represents a frequency ratio of , or 38.71 cents (). 31-ET is a very good approximation of quarter-comma meantone temperament. More generally, it is a regular diatonic tuning in which the tempered perfect fifth is equal to 696.77 cents, as shown in Figure 1. On an isomorphic keyboard, the fingering of music composed in 31-ET is precisely the same as it is in any other syntonic tuning (such as 12-ET), so long as the notes are spelled properly — that is, with no assumption of enharmonicity. History and use Division of the octave into 31 steps arose naturally out of Renaissance music theory; the lesser diesis — the ratio of an octave to three major thirds, 128:125 or 41.06 cents — was approxima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adriaan Fokker
Adriaan Daniël Fokker (; 17 August 1887 – 24 September 1972) was a Dutch physicist. He worked in the fields of special relativity and statistical mechanics. He was the inventor of the Fokker organ, a 31-tone equal-tempered (31-TET) organ. Life and work Adriaan Daniël Fokker was born on 17 August 1887 in Buitenzorg, Dutch East Indies (now Bogor, Indonesia). He was a cousin of the aeronautical engineer Anthony Fokker. Fokker studied mining engineering at the Delft University of Technology and physics at the University of Leiden with Hendrik Lorentz, where he earned his doctorate in 1913. He continued his studies with Albert Einstein, Ernest Rutherford and William Bragg. In his 1913 thesis, he derived the Fokker–Planck equation along with Max Planck. After his military service during World War I he returned to Leiden as Lorentz' and Ehrenfest's assistant. Fokker became a physics teacher at the Gymnasium of Delft after 1918 and was appointed in 1923 as the first profes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval (music)
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord. In Western music, intervals are most commonly differences between notes of a diatonic scale. Intervals between successive notes of a scale are also known as scale steps. The smallest of these intervals is a semitone. Intervals smaller than a semitone are called microtones. They can be formed using the notes of various kinds of non-diatonic scales. Some of the very smallest ones are called commas, and describe small discrepancies, observed in some tuning systems, between enharmonically equivalent notes such as C and D. Intervals can be arbitrarily small, and even imperceptible to the human ear. In physical terms, an interval is the ratio between two sonic fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Microtonal Music
Microtonal music or microtonality is the use in music of microtones— intervals smaller than a semitone, also called "microintervals". It may also be extended to include any music using intervals not found in the customary Western tuning of twelve equal intervals per octave. In other words, a microtone may be thought of as a note that falls between the keys of a piano tuned in equal temperament. In ''Revising the musical equal temperament,'' Haye Hinrichsen defines equal temperament as “the frequency ratios of all intervals are invariant under transposition (translational shifts along the keyboard), i.e., to be constant. The standard twelve-tone ''equal temperament'' (ET), which was originally invented in ancient China and rediscovered in Europe in the 16th century, is determined by two additional conditions. Firstly the octave is divided into twelve semitones. Secondly the octave, the most fundamental of all intervals, is postulated to be pure (beatless), as described by t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Septimal Kleisma
In music, the ratio 225/224 is called the septimal kleisma (). It is a minute comma type interval of approximately 7.7 cents. Factoring it into primes gives 2−5 32 52 7−1, which can be rewritten 2−1 (5/4)2 (9/7). That says that it is the amount that two major thirds of 5/4 and a septimal major third In music, the septimal major third , also called the supermajor third (by Hermann von Helmholtz among others Hermann L. F. von Helmholtz (2007). ''Sensations of Tone'', p. 187. .) and sometimes '' Bohlen–Pierce third'' is the musical interval ..., or supermajor third, of 9/7 exceeds the octave. The septimal kleisma can also be viewed as the difference between the diatonic semitone (16:15) and the septimal diatonic semitone (15:14). References {{Intervals, state=expanded 7-limit tuning and intervals Commas (music) 0225:0224 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Septimal Semicomma
In music, the septimal semicomma, a seven-limit semicomma, is the ratio 126/125 and is equal to approximately 13.79 cents (). It is also called the ''small septimal comma''Haluska, Jan (2003). ''The Mathematical Theory of Tone Systems'', p.xxvi. . and the ''starling comma'' after its use in starling temperament. Factored into primes it is: 2*3^2*5^*7 Or as simple just intervals: (6/5)^3*(7/6)*(2/1)^ Thus it is the difference between three minor thirds of 6/5 plus a septimal minor third of 7/6 and an octave (2/1). This comma is important to certain tuning systems, such as septimal meantone temperament. A diminished seventh chord consisting of three minor thirds and a subminor third making up an octave is possible in such systems. This characteristic feature of these tuning systems is known as the ''septimal semicomma diminished seventh chord''. In equal temperament It is tempered out in 19 equal temperament and 31 equal temperament, but not in 22 equal temperament, 34 equal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
5-limit Tuning And Intervals
Five-limit tuning, 5-limit tuning, or 5-prime-limit tuning (not to be confused with 5-odd-limit tuning), is any system for tuning a musical instrument that obtains the frequency of each note by multiplying the frequency of a given reference note (the base note) by products of integer powers of 2, 3, or 5 (prime numbers limited to 5 or lower), such as . Powers of 2 represent intervallic movements by octaves. Powers of 3 represent movements by intervals of perfect fifths (plus one octave, which can be removed by multiplying by 1/2, i.e., 2−1). Powers of 5 represent intervals of major thirds (plus two octaves, removable by multiplying by 1/4, i.e., 2−2). Thus, 5-limit tunings are constructed entirely from stacking of three basic purely-tuned intervals (octaves, thirds and fifths). Since the perception of consonance seems related to low numbers in the harmonic series, and 5-limit tuning relies on the three lowest primes, 5-limit tuning should be capable of producing very consona ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |