|
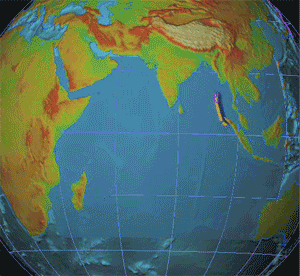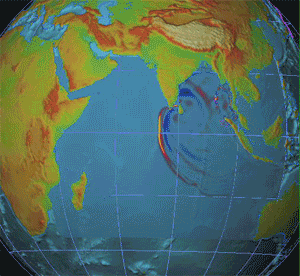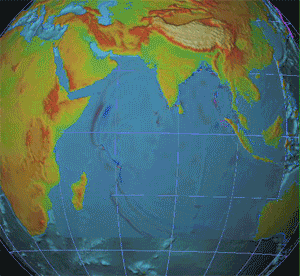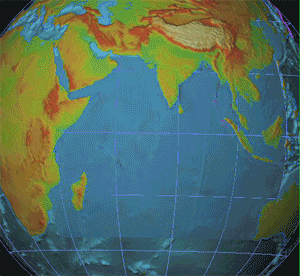
S Waves
__NOTOC__ In seismology and other areas involving elastic waves, S waves, secondary waves, or shear waves (sometimes called elastic S waves) are a type of elastic wave and are one of the two main types of elastic body waves, so named because they move through the body of an object, unlike surface waves. S waves are transverse waves, meaning that the direction of particle movement of an S wave is perpendicular to the direction of wave propagation, and the main restoring force comes from shear stress. Therefore, S waves cannot propagate in liquids with zero (or very low) viscosity; however, they may propagate in liquids with high viscosity. Similarly, S waves cannot travel through gases. The name ''secondary wave'' comes from the fact that they are the second type of wave to be detected by an earthquake seismograph, after the compressional primary wave, or P wave, because S waves travel more slowly in solids. Unlike P waves, S waves cannot travel through the molten outer core ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seismology
Seismology (; from Ancient Greek σεισμός (''seismós'') meaning "earthquake" and -λογία (''-logía'') meaning "study of") is the scientific study of earthquakes (or generally, quakes) and the generation and propagation of elastic waves through planetary bodies. It also includes studies of the environmental effects of earthquakes such as tsunamis; other seismic sources such as volcanoes, plate tectonics, glaciers, rivers, oceanic microseisms, and the atmosphere; and artificial processes such as explosions. Paleoseismology is a related field that uses geology to infer information regarding past earthquakes. A recording of Earth's motion as a function of time, created by a seismograph is called a seismogram. A seismologist is a scientist who works in basic or applied seismology. History Scholarly interest in earthquakes can be traced back to antiquity. Early speculations on the natural causes of earthquakes were included in the writings of Thales of Miletu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Speeds Of Seismic Waves
In kinematics, the speed (commonly referred to as ''v'') of an object is the magnitude of the change of its position over time or the magnitude of the change of its position per unit of time; it is thus a non-negative scalar quantity. Introduction of the speed/velocity terminology by Prof. Tait, in 1882. The average speed of an object in an interval of time is the distance travelled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as the duration of the time interval approaches zero. Speed is the magnitude of ''velocity'' (a vector), which indicates additionally the direction of motion. Speed has the dimensions of distance divided by time. The SI unit of speed is the metre per second (m/s), but the most common unit of speed in everyday usage is the kilometre per hour (km/h) or, in the US and the UK, miles per hour (mph). For air and marine travel, the knot is commonly used. The fastest possible speed at which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nabla Operator
Del, or nabla, is an operator used in mathematics (particularly in vector calculus) as a vector differential operator, usually represented by the nabla symbol ∇. When applied to a function defined on a one-dimensional domain, it denotes the standard derivative of the function as defined in calculus. When applied to a ''field'' (a function defined on a multi-dimensional domain), it may denote any one of three operations depending on the way it is applied: the gradient or (locally) steepest slope of a scalar field (or sometimes of a vector field, as in the Navier–Stokes equations); the divergence of a vector field; or the curl (rotation) of a vector field. Del is a very convenient mathematical notation for those three operations (gradient, divergence, and curl) that makes many equations easier to write and remember. The del symbol (or nabla) can be formally defined as a vector operator whose components are the corresponding partial derivative operators. As a ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be used: \rho = \frac, where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate this quantity is more specifically called specific weight. For a pure substance, the density is equal to its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium is the densest known element at standard conditions for temperature and pressure. To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity "relative den ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's 2nd Law
Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows: # A body remains at rest, or in motion at a constant speed in a straight line, unless it is acted upon by a force. # At any instant of time, the net force on a body is equal to the body's acceleration multiplied by its mass or, equivalently, the rate at which the body's momentum is changing with time. # If two bodies exert forces on each other, these forces have the same magnitude but opposite directions. The three laws of motion were first stated by Isaac Newton in his ''Philosophiæ Naturalis Principia Mathematica'' (''Mathematical Principles of Natural Philosophy''), originally published in 1687. Newton used them to investigate and explain the motion of many physical objects and systems. In the time since Newton, new insights, especially around t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Modulus
In materials science, shear modulus or modulus of rigidity, denoted by ''G'', or sometimes ''S'' or ''μ'', is a measure of the Elasticity (physics), elastic shear stiffness of a material and is defined as the ratio of shear stress to the shear strain: :G \ \stackrel\ \frac = \frac = \frac where :\tau_ = F/A \, = shear stress :F is the force which acts :A is the area on which the force acts :\gamma_ = shear strain. In engineering :=\Delta x/l = \tan \theta , elsewhere := \theta :\Delta x is the transverse displacement :l is the initial length of the area. The derived SI unit of shear modulus is the Pascal (unit), pascal (Pa), although it is usually expressed in Pascal (unit), gigapascals (GPa) or in thousand pounds per square inch (ksi). Its dimensional analysis, dimensional form is M1L−1T−2, replacing ''force'' by ''mass'' times ''acceleration''. Explanation The shear modulus is one of several quantities for measuring the stiffness of materials. All of them arise in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lamé Parameters
In continuum mechanics, Lamé parameters (also called the Lamé coefficients, Lamé constants or Lamé moduli) are two material-dependent quantities denoted by ''λ'' and ''μ'' that arise in strain- stress relationships. In general, ''λ'' and ''μ'' are individually referred to as ''Lamé's first parameter'' and ''Lamé's second parameter'', respectively. Other names are sometimes employed for one or both parameters, depending on context. For example, the parameter ''μ'' is referred to in fluid dynamics as the dynamic viscosity of a fluid (not expressed in the same units); whereas in the context of elasticity, ''μ'' is called the shear modulus, and is sometimes denoted by ''G'' instead of ''μ''. Typically the notation ''G'' is seen paired with the use of Young's modulus ''E'', and the notation ''μ'' is paired with the use of ''λ''. In homogeneous and isotropic materials, these define Hooke's law in 3D, \boldsymbol = 2\mu \boldsymbol + \lambda \; \operatorname(\boldsymbo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kronecker Delta
In mathematics, the Kronecker delta (named after Leopold Kronecker) is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise: \delta_ = \begin 0 &\text i \neq j, \\ 1 &\text i=j. \end or with use of Iverson brackets: \delta_ = =j, For example, \delta_ = 0 because 1 \ne 2, whereas \delta_ = 1 because 3 = 3. The Kronecker delta appears naturally in many areas of mathematics, physics, engineering and computer science, as a means of compactly expressing its definition above. Generalized versions of the Kronecker delta have found applications in differential geometry and modern tensor calculus, particularly in formulations of gauge theory and topological field models. In linear algebra, the n\times n identity matrix \mathbf has entries equal to the Kronecker delta: I_ = \delta_ where i and j take the values 1,2,\cdots,n, and the inner product of vectors can be written as \mathbf\cdot\mathbf = \sum_^n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Stress Tensor
In continuum mechanics, the Cauchy stress tensor (symbol \boldsymbol\sigma, named after Augustin-Louis Cauchy), also called true stress tensor or simply stress tensor, completely defines the state of stress at a point inside a material in the deformed state, placement, or configuration. The second order tensor consists of nine components \sigma_ and relates a unit-length direction vector e to the ''traction vector'' T(e) across an imaginary surface perpendicular to e: :\mathbf^ = \mathbf e \cdot\boldsymbol\quad \text \quad T_^= \sum_\sigma_e_i. The SI base units of both stress tensor and traction vector are newton per square metre (N/m2) or pascal (Pa), corresponding to the stress scalar. The unit vector is dimensionless. The Cauchy stress tensor obeys the tensor transformation law under a change in the system of coordinates. A graphical representation of this transformation law is the Mohr's circle for stress. The Cauchy stress tensor is used for stress analysis of mater ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strain Tensor
In mechanics, strain is defined as relative deformation, compared to a position configuration. Different equivalent choices may be made for the expression of a strain field depending on whether it is defined with respect to the initial or the final configuration of the body and on whether the metric tensor or its dual is considered. Strain has dimension of a length ratio, with SI base units of meter per meter (m/m). Hence strains are dimensionless and are usually expressed as a decimal fraction or a percentage. Parts-per notation is also used, e.g., parts per million or parts per billion (sometimes called "microstrains" and "nanostrains", respectively), corresponding to μm/m and nm/m. Strain can be formulated as the spatial derivative of displacement: \boldsymbol \doteq \cfrac\left(\mathbf - \mathbf\right) = \boldsymbol'- \boldsymbol, where is the identity tensor. The displacement of a body may be expressed in the form , where is the reference position of material po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set (mathematics), set to a set assigns to each element of exactly one element of .; the words ''map'', ''mapping'', ''transformation'', ''correspondence'', and ''operator'' are sometimes used synonymously. The set is called the Domain of a function, domain of the function and the set is called the codomain of the function. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. History of the function concept, Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable function, differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly increased the possible applications of the concept. A f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector (mathematics)
In mathematics and physics, vector is a term that refers to quantities that cannot be expressed by a single number (a scalar), or to elements of some vector spaces. Historically, vectors were introduced in geometry and physics (typically in mechanics) for quantities that have both a magnitude and a direction, such as displacements, forces and velocity. Such quantities are represented by geometric vectors in the same way as distances, masses and time are represented by real numbers. The term ''vector'' is also used, in some contexts, for tuples, which are finite sequences (of numbers or other objects) of a fixed length. Both geometric vectors and tuples can be added and scaled, and these vector operations led to the concept of a vector space, which is a set equipped with a vector addition and a scalar multiplication that satisfy some axioms generalizing the main properties of operations on the above sorts of vectors. A vector space formed by geometric vectors is called a Euc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |