|
Risk Assessment
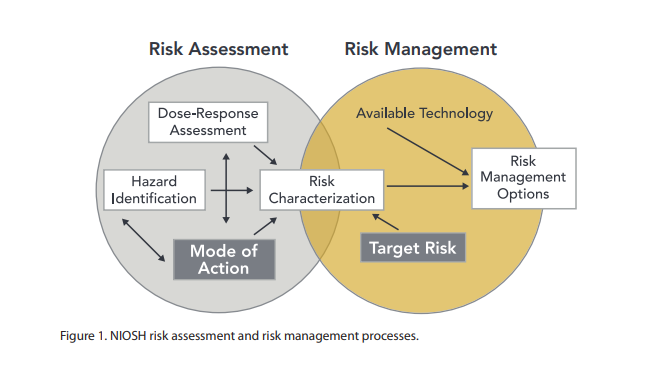
Risk assessment is a process for identifying hazards, potential (future) events which may negatively impact on individuals, assets, and/or the environment because of those hazards, their likelihood and consequences, and actions which can mitigate these effects. The output from such a process may also be called a risk assessment. Hazard analysis forms the first stage of a risk assessment process. Judgments "on the tolerability of the risk on the basis of a risk analysis" (i.e. risk evaluation) also form part of the process. The results of a risk assessment process may be expressed in a quantitative or qualitative fashion. Risk assessment forms a key part of a broader risk management strategy to help reduce any potential risk-related consequences. Categories Individual risk assessment Risk assessments can be undertaken in individual cases, including in patient and physician interactions. In the narrow sense chemical risk assessment is the assessment of a health risk in response ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hazard Analysis
A hazard analysis is one of many methods that may be used to assess risk. At its core, the process entails describing a system object (such as a person or machine) that intends to conduct some activity. During the performance of that activity, an adverse event (referred to as a “ factor”) may be encountered that could cause or contribute to an occurrence (mishap, incident, accident). Finally, that occurrence will result in some outcome that may be measured in terms of the degree of loss or harm. This outcome may be measured on a continuous scale, such as an amount of monetary loss, or the outcomes may be categorized into various levels of severity. A Simple Hazard Analysis The first step in hazard analysis is to identify the hazards. If an automobile is an object performing an activity such as driving over a bridge, and that bridge may become icy, then an icy bridge might be identified as a hazard. If this hazard is encountered, it could cause or contribute to the occur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Services
Social services are a range of public services intended to provide support and assistance towards particular groups, which commonly include the disadvantaged. Also available amachine-converted HTML They may be provided by individuals, private and independent organizations, or administered by a government agency. Social services are connected with the concept of welfare and the welfare state, as countries with large welfare programs often provide a wide range of social services. Social services are employed to address the wide range of needs of a society. Prior to industrialisation, the provision of social services was largely confined to private organisations and charities, with the extent of its coverage also limited. Social services are now generally regarded globally as a 'necessary function' of society and a mechanism through which governments may address societal issues. The provision of social services by governments is linked to the belief of Human rights, universal human rig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, unlike the standard deviation, its units differ from the random variable, which is why the standard devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power-law Distributions
In statistics, a power law is a functional relationship between two quantities, where a relative change in one quantity results in a relative change in the other quantity proportional to the change raised to a constant exponent: one quantity varies as a power of another. The change is independent of the initial size of those quantities. For instance, the area of a square has a power law relationship with the length of its side, since if the length is doubled, the area is multiplied by 2, while if the length is tripled, the area is multiplied by 3, and so on. Empirical examples The distributions of a wide variety of physical, biological, and human-made phenomena approximately follow a power law over a wide range of magnitudes: these include the sizes of craters on the moon and of solar flares, cloud sizes, the foraging pattern of various species, the sizes of activity patterns of neuronal populations, the frequencies of words in most languages, frequencies of family names, the spe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pareto Distribution
The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto, is a power-law probability distribution that is used in description of social, quality control, scientific, geophysical, actuarial science, actuarial, and many other types of observable phenomena; the principle originally applied to describing the distribution of wealth in a society, fitting the trend that a large portion of wealth is held by a small fraction of the population. The ''Pareto principle'' or "80:20 rule" stating that 80% of outcomes are due to 20% of causes was named in honour of Pareto, but the concepts are distinct, and only Pareto distributions with shape value () precisely reflect it. Empirical observation has shown that this 80:20 distribution fits a wide range of cases, including natural phenomena and human activities. Definitions If ''X'' is a random variable with a Pareto (Type I) distribution, then the probability that ''X'' is greater than some nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fat-tailed Distribution
A fat-tailed distribution is a probability distribution that exhibits a large skewness or kurtosis, relative to that of either a normal distribution or an exponential distribution. In common usage, the terms fat-tailed and Heavy-tailed distribution, heavy-tailed are sometimes synonymous; fat-tailed is sometimes also defined as a subset of heavy-tailed. Different research communities favor one or the other largely for historical reasons, and may have differences in the precise definition of either. Fat-tailed distributions have been empirically encountered in a variety of areas: physics, earth sciences, economics and political science. The class of fat-tailed distributions includes those whose tails decay like a power law, which is a common point of reference in their use in the scientific literature. However, fat-tailed distributions also include other slowly-decaying distributions, such as the log-normal distribution, log-normal. The extreme case: a power-law distribution The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Law Of Large Numbers
In probability theory, the law of large numbers is a mathematical law that states that the average of the results obtained from a large number of independent random samples converges to the true value, if it exists. More formally, the law of large numbers states that given a sample of independent and identically distributed values, the sample mean converges to the true mean. The law of large numbers is important because it guarantees stable long-term results for the averages of some random events. For example, while a casino may lose money in a single spin of the roulette wheel, its earnings will tend towards a predictable percentage over a large number of spins. Any winning streak by a player will eventually be overcome by the parameters of the game. Importantly, the law applies (as the name indicates) only when a ''large number'' of observations are considered. There is no principle that a small number of observations will coincide with the expected value or that a stre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regression Toward The Mean
In statistics, regression toward the mean (also called regression to the mean, reversion to the mean, and reversion to mediocrity) is the phenomenon where if one sample of a random variable is extreme, the next sampling of the same random variable is likely to be closer to its mean. Furthermore, when many random variables are sampled and the most extreme results are intentionally picked out, it refers to the fact that (in many cases) a second sampling of these picked-out variables will result in "less extreme" results, closer to the initial mean of all of the variables. Mathematically, the strength of this "regression" effect is dependent on whether or not all of the random variables are drawn from the same distribution, or if there are genuine differences in the underlying distributions for each random variable. In the first case, the "regression" effect is statistically likely to occur, but in the second case, it may occur less strongly or not at all. Regression toward the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is f(x) = \frac e^\,. The parameter is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma^2 is the variance. The standard deviation of the distribution is (sigma). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |