|
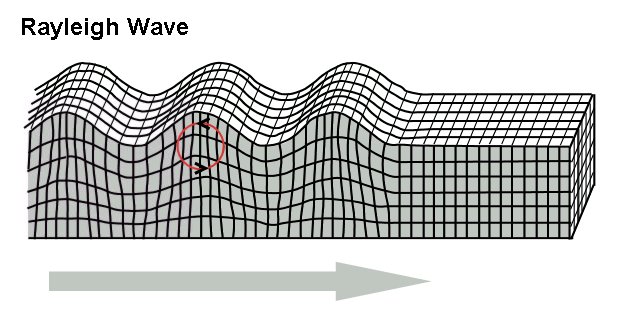
Rayleigh Wave
Rayleigh waves are a type of surface acoustic wave that travel along the surface of solids. They can be produced in materials in many ways, such as by a localized impact or by Piezoelectricity, piezo-electric Interdigital transducer, transduction, and are frequently used in non-destructive testing for detecting defects. Rayleigh waves are part of the seismic waves that are produced on the Earth by earthquakes. When guided in layers they are referred to as Lamb waves, Rayleigh–Lamb waves, or generalized Rayleigh waves. Characteristics Rayleigh waves are a type of surface wave that travel near the surface of solids. Rayleigh waves include both longitudinal and transverse motions that decrease exponentially in amplitude as distance from the surface increases. There is a phase difference between these component motions. The existence of Rayleigh waves was predicted in 1885 by Lord Rayleigh, after whom they were named. In isotropic solids these waves cause the surface particles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Acoustic Wave
A surface acoustic wave (SAW) is an acoustic wave traveling along the surface of a material exhibiting elastic (solid mechanics), elasticity, with an amplitude that typically decays exponentially with depth into the material, such that they are confined to a depth of about one wavelength. Discovery SAWs were first explained in 1885 by Lord Rayleigh, who described the surface acoustic mode of propagation and predicted its properties in his classic paper. Named after their discoverer, Rayleigh waves have a Longitudinal wave, longitudinal and a vertical shear component that can couple with any media like additional layers in contact with the surface. This coupling strongly affects the amplitude and velocity of the wave, allowing SAW sensors to directly sense mass and mechanical properties. The term 'Rayleigh waves' is often used synonymously with 'SAWs', although strictly speaking there are multiple types of surface acoustic waves, such as Love waves, which are Polarization (waves), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Love Wave
In elastodynamics, Love waves, named after Augustus Edward Hough Love, are horizontally polarized surface waves. The Love wave is a result of the interference of many shear waves ( S-waves) guided by an elastic layer, which is ''welded'' to an elastic half space on one side while bordering a vacuum on the other side. In seismology, Love waves (also known as Q waves (, "lateral" in German) are surface seismic waves that cause horizontal shifting of the Earth during an earthquake. Augustus Edward Hough Love predicted the existence of Love waves mathematically in 1911. They form a distinct class, different from other types of seismic waves, such as P-waves and S-waves (both body waves), or Rayleigh waves (another type of surface wave). Love waves travel with a lower velocity than P- or S- waves, but faster than Rayleigh waves. These waves are observed only when there is a low velocity layer overlying a high velocity layer/sub–layers. Description The particle motion of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be used: \rho = \frac, where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate this quantity is more specifically called specific weight. For a pure substance, the density is equal to its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium is the densest known element at standard conditions for temperature and pressure. To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity "relative den ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Train
In physics, a wave packet (also known as a wave train or wave group) is a short burst of localized wave action that travels as a unit, outlined by an envelope. A wave packet can be analyzed into, or can be synthesized from, a potentially-infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere. Any signal of a limited width in time or space requires many frequency components around a center frequency within a bandwidth inversely proportional to that width; even a gaussian function is considered a wave packet because its Fourier transform is a "packet" of waves of frequencies clustered around a central frequency. Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant (no dispersion) or it may change ( dispersion) while propagati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Velocity Dispersion
In astronomy, the velocity dispersion (''σ'') is the statistical dispersion of velocities about the mean velocity for a group of astronomical objects, such as an open cluster, globular cluster, galaxy, galaxy cluster, or supercluster. By measuring the radial velocities of the group's members through astronomical spectroscopy, the velocity dispersion of that group can be estimated and used to derive the group's mass from the virial theorem.Collins Dictionary of Astronomy, 2nd Ed.; Harper Collins Publishers; 2000; pp. 444, 449 Radial velocity is found by measuring the Doppler width of spectral lines of a collection of objects; the more radial velocities one measures, the more accurately one knows their dispersion. A ''central velocity dispersion'' refers to the σ of the interior regions of an extended object, such as a galaxy or cluster. The relationship between velocity dispersion and matter (or the observed electromagnetic radiation emitted by this matter) takes several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio signals (sound), radio waves, and light. The interval of time between events is called the period. It is the reciprocal of the frequency. For example, if a heart beats at a frequency of 120 times per minute (2 hertz), its period is one half of a second. Special definitions of frequency are used in certain contexts, such as the angular frequency in rotational or cyclical properties, when the rate of angular progress is measured. Spatial frequency is defined for properties that vary or cccur repeatedly in geometry or space. The unit of measurement of frequency in the International System of Units (SI) is the hertz, having the symbol Hz. Definitions and units For cyclical phenomena such as oscillations, waves, or for examp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Value Problem
In the study of differential equations, a boundary-value problem is a differential equation subjected to constraints called boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions. Boundary value problems arise in several branches of physics as any physical differential equation will have them. Problems involving the wave equation, such as the determination of normal modes, are often stated as boundary value problems. A large class of important boundary value problems are the Sturm–Liouville problems. The analysis of these problems, in the linear case, involves the eigenfunctions of a differential operator. To be useful in applications, a boundary value problem should be well posed. This means that given the input to the problem there exists a unique solution, which depends continuously on the input. Much theoretical work in the field of partial differential equations is devot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lamé Parameters
In continuum mechanics, Lamé parameters (also called the Lamé coefficients, Lamé constants or Lamé moduli) are two material-dependent quantities denoted by ''λ'' and ''μ'' that arise in strain- stress relationships. In general, ''λ'' and ''μ'' are individually referred to as ''Lamé's first parameter'' and ''Lamé's second parameter'', respectively. Other names are sometimes employed for one or both parameters, depending on context. For example, the parameter ''μ'' is referred to in fluid dynamics as the dynamic viscosity of a fluid (not expressed in the same units); whereas in the context of elasticity, ''μ'' is called the shear modulus, and is sometimes denoted by ''G'' instead of ''μ''. Typically the notation ''G'' is seen paired with the use of Young's modulus ''E'', and the notation ''μ'' is paired with the use of ''λ''. In homogeneous and isotropic materials, these define Hooke's law in 3D, \boldsymbol = 2\mu \boldsymbol + \lambda \; \operatorname(\boldsymbo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wind Wave
In fluid dynamics, a wind wave, or wind-generated water wave, is a surface wave that occurs on the free surface of bodies of water as a result of the wind blowing over the water's surface. The contact distance in the direction of the wind is known as the '' fetch''. Waves in the oceans can travel thousands of kilometers before reaching land. Wind waves on Earth range in size from small ripples to waves over high, being limited by wind speed, duration, fetch, and water depth. When directly generated and affected by local wind, a wind wave system is called a wind sea. Wind waves will travel in a great circle route after being generated – curving slightly left in the southern hemisphere and slightly right in the northern hemisphere. After moving out of the area of fetch and no longer being affected by the local wind, wind waves are called '' swells'' and can travel thousands of kilometers. A noteworthy example of this is waves generated south of Tasmania during heavy wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seismology
Seismology (; from Ancient Greek σεισμός (''seismós'') meaning "earthquake" and -λογία (''-logía'') meaning "study of") is the scientific study of earthquakes (or generally, quakes) and the generation and propagation of elastic waves through planetary bodies. It also includes studies of the environmental effects of earthquakes such as tsunamis; other seismic sources such as volcanoes, plate tectonics, glaciers, rivers, oceanic microseisms, and the atmosphere; and artificial processes such as explosions. Paleoseismology is a related field that uses geology to infer information regarding past earthquakes. A recording of Earth's motion as a function of time, created by a seismograph is called a seismogram. A seismologist is a scientist who works in basic or applied seismology. History Scholarly interest in earthquakes can be traced back to antiquity. Early speculations on the natural causes of earthquakes were included in the writings of Thales of Miletu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson's Ratio
In materials science and solid mechanics, Poisson's ratio (symbol: ( nu)) is a measure of the Poisson effect, the deformation (expansion or contraction) of a material in directions perpendicular to the specific direction of loading. The value of Poisson's ratio is the negative of the ratio of transverse strain to axial strain. For small values of these changes, is the amount of transversal elongation divided by the amount of axial compression. Most materials have Poisson's ratio values ranging between 0.0 and 0.5. For soft materials, such as rubber, where the bulk modulus is much higher than the shear modulus, Poisson's ratio is near 0.5. For open-cell polymer foams, Poisson's ratio is near zero, since the cells tend to collapse in compression. Many typical solids have Poisson's ratios in the range of 0.2 to 0.3. The ratio is named after the French mathematician and physicist Siméon Poisson. Origin Poisson's ratio is a measure of the Poisson effect, the phenomenon in whi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |