|
Potential Of Mean Force
When examining a system computationally one may be interested in knowing how the free energy changes as a function of some inter- or intramolecular coordinate (such as the distance between two atoms or a torsional angle). The free energy surface along the chosen coordinate is referred to as the potential of mean force (PMF). If the system of interest is in a solvent, then the PMF also incorporates the solvent effects. General description The PMF can be obtained in Monte Carlo or molecular dynamics simulations to examine how a system's energy changes as a function of some specific reaction coordinate parameter. For example, it may examine how the system's energy changes as a function of the distance between two residues, or as a protein is pulled through a lipid bilayer. It can be a geometrical coordinate or a more general energetic (solvent) coordinate. Often PMF simulations are used in conjunction with umbrella sampling, because typically the PMF simulation will fail to adequately s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Dynamics
Molecular dynamics (MD) is a computer simulation method for analyzing the physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamic "evolution" of the system. In the most common version, the trajectories of atoms and molecules are determined by numerically solving Newton's equations of motion for a system of interacting particles, where forces between the particles and their potential energies are often calculated using interatomic potentials or molecular mechanical force fields. The method is applied mostly in chemical physics, materials science, and biophysics. Because molecular systems typically consist of a vast number of particles, it is impossible to determine the properties of such complex systems analytically; MD simulation circumvents this problem by using numerical methods. However, long MD simulations are mathematically ill-conditioned, generating cumulative errors in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Umbrella Sampling
Umbrella sampling is a technique in computational physics and chemistry, used to improve sampling of a system (or different systems) where ergodicity is hindered by the form of the system's energy landscape. It was first suggested by Torrie and Valleau in 1977. It is a particular physical application of the more general importance sampling in statistics. Systems in which an energy barrier separates two regions of configuration space may suffer from poor sampling. In Metropolis Monte Carlo runs, the low probability of overcoming the potential barrier can leave inaccessible configurations poorly sampled—or even entirely unsampled—by the simulation. An easily visualised example occurs with a solid at its melting point: considering the state of the system with an order parameter ''Q'', both liquid (low ''Q'') and solid (high ''Q'') phases are low in energy, but are separated by a free energy barrier at intermediate values of ''Q''. This prevents the simulation from adequately sa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radial Distribution Function
In statistical mechanics, the radial distribution function, (or pair correlation function) g(r) in a system of particles (atoms, molecules, colloids, etc.), describes how density varies as a function of distance from a reference particle. If a given particle is taken to be at the origin O, and if \rho =N/V is the average number density of particles, then the local time-averaged density at a distance r from O is \rho g(r). This simplified definition holds for a homogeneous and isotropic system. A more general case will be considered below. In simplest terms it is a measure of the probability of finding a particle at a distance of r away from a given reference particle, relative to that for an ideal gas. The general algorithm involves determining how many particles are within a distance of r and r+dr away from a particle. This general theme is depicted to the right, where the red particle is our reference particle, and blue particles are those whose centers are within the circul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Inversion Method
Ludwig Eduard Boltzmann (; 20 February 1844 – 5 September 1906) was an Austrian physicist and philosopher. His greatest achievements were the development of statistical mechanics, and the statistical explanation of the second law of thermodynamics. In 1877 he provided the current definition of entropy, S = k_ \ln \Omega \!, where Ω is the number of microstates whose energy equals the system's energy, interpreted as a measure of statistical disorder of a system. Max Planck named the constant the Boltzmann constant. Statistical mechanics is one of the pillars of modern physics. It describes how macroscopic observations (such as temperature and pressure) are related to microscopic parameters that fluctuate around an average. It connects thermodynamic quantities (such as heat capacity) to microscopic behavior, whereas, in classical thermodynamics, the only available option would be to measure and tabulate such quantities for various materials. Biography Childhood and educatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Potential
In protein structure prediction, statistical potentials or knowledge-based potentials are scoring functions derived from an analysis of known protein structures in the Protein Data Bank (PDB). The original method to obtain such potentials is the ''quasi-chemical approximation'', due to Miyazawa and Jernigan. It was later followed by the ''potential of mean force'' (statistical PMF ), developed by Sippl. Although the obtained scores are often considered as approximations of the free energy—thus referred to as ''pseudo-energies''—this physical interpretation is incorrect. Nonetheless, they are applied with success in many cases, because they frequently correlate with actual Gibbs free energy differences. Overview Possible features to which a pseudo-energy can be assigned include: * interatomic distances, * torsion angles, * solvent exposure, * or hydrogen bond geometry. The classic application is, however, based on pairwise amino acid contacts or distances, thus producing s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Energy Perturbation
Free energy perturbation (FEP) is a method based on statistical mechanics that is used in computational chemistry for computing free energy differences from molecular dynamics or Metropolis Monte Carlo simulations. The FEP method was introduced by Robert W. Zwanzig in 1954. According to the free-energy perturbation method, the free energy difference for going from state A to state B is obtained from the following equation, known as the ''Zwanzig equation'': :\Delta F(\mathbf \rightarrow \mathbf) = F_\mathbf - F_\mathbf = -k_\mathrm T \ln \left \langle \exp \left ( - \frac \right ) \right \rangle _\mathbf where ''T'' is the temperature, ''k''B is Boltzmann's constant, and the angular brackets denote an average over a simulation run for state A. In practice, one runs a normal simulation for state A, but each time a new configuration is accepted, the energy for state B is also computed. The difference between states A and B may be in the atom types involved, in which case the Δ''F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
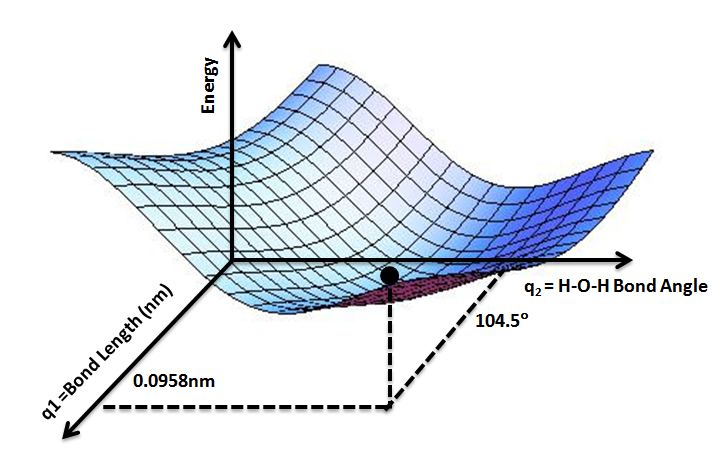
Potential Energy Surface
A potential energy surface (PES) describes the energy of a system, especially a collection of atoms, in terms of certain parameters, normally the positions of the atoms. The surface might define the energy as a function of one or more coordinates; if there is only one coordinate, the surface is called a ''potential energy curve'' or energy profile. An example is the Morse/Long-range potential. It is helpful to use the analogy of a landscape: for a system with two degrees of freedom (e.g. two bond lengths), the value of the energy (analogy: the height of the land) is a function of two bond lengths (analogy: the coordinates of the position on the ground). The PES concept finds application in fields such as chemistry and physics, especially in the theoretical sub-branches of these subjects. It can be used to theoretically explore properties of structures composed of atoms, for example, finding the minimum energy shape of a molecule or computing the rates of a chemical reaction. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
David Chandler (chemist)
David Chandler (October 15, 1944 – April 18, 2017) was a physical chemist and a professor at the University of California, Berkeley. He was a member of the United States National Academy of Sciences and a winner of the Irving Langmuir Award. He published two books and over 300 scientific articles. Biography Chandler was born in New York City in 1944. He was the Bruce H. Mahan Professor of Chemistry at the University of California, Berkeley. He received his S.B. degree in chemistry from MIT in 1966, and his Ph.D. in chemical Physics at Harvard in 1969. He began his academic career as an assistant professor in 1970 at the University of Illinois, Urbana-Champaign, rising through the ranks to become a full professor in 1977. Prior to joining the Berkeley faculty in 1986, Chandler spent two years as professor of chemistry at the University of Pennsylvania. Chandler's primary area of research was statistical mechanics. With it, he created many of the basic techniques with which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Introduction To Modern Statistical Mechanics
Introduction, The Introduction, Intro, or The Intro may refer to: General use * Introduction (music), an opening section of a piece of music * Introduction (writing), a beginning section to a book, article or essay which states its purpose and goals ** Foreword, a beginning section * Introduction (British House of Commons), a ceremonial seating for members elected in by-elections * Introduction (House of Lords), a ceremonial seating for some new members * Intro (demoscene), in the demoscene, a short computer program produced for promotion or to meet competition requirements * Introduced species or introduction, a species established by humans outside its natural range * Right of initiative (legislative), the ability of an entity to introduce a bill or other proposed legislation before a Legislature. * Product launch, the introduction of a new product to market Music Performers * Intro (R&B group), an American R&B trio *Introduction (rock band), a Swedish rock group Albums * '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |