|
Prouhet–Tarry–Escott Problem
In mathematics, the Prouhet–Tarry–Escott problem asks for two disjoint multisets ''A'' and ''B'' of ''n'' integers each, whose first ''k'' power sum symmetric polynomials are all equal. That is, the two multisets should satisfy the equations :\sum_ a^i = \sum_ b^i for each integer ''i'' from 1 to a given ''k''. It has been shown that ''n'' must be strictly greater than ''k''. Solutions with k = n - 1 are called ''ideal solutions''. Ideal solutions are known for 3 \le n \le 10 and for n = 12. No ideal solution is known for n=11 or for n \ge 13. This problem was named after Eugène Prouhet, who studied it in the early 1850s, and Gaston Tarry and Edward B. Escott, who studied it in the early 1910s. The problem originates from letters of Christian Goldbach and Leonhard Euler (1750/1751). Examples Ideal solutions An ideal solution for ''n'' = 6 is given by the two sets and , because: : 01 + 51 + 61 + 161 + 171 + 221 = 11 + 21 + 101 + 121 + 201 + 211 : 02 + 5 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Integers
In number theory, a Gaussian integer is a complex number whose real and imaginary parts are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as \mathbf /math> or \Z Gaussian integers share many properties with integers: they form a Euclidean domain, and thus have a Euclidean division and a Euclidean algorithm; this implies unique factorization and many related properties. However, Gaussian integers do not have a total order that respects arithmetic. Gaussian integers are algebraic integers and form the simplest ring of quadratic integers. Gaussian integers are named after the German mathematician Carl Friedrich Gauss. Basic definitions The Gaussian integers are the set :\mathbf \, \qquad \text i^2 = -1. In other words, a Gaussian integer is a complex number such that its real and imaginary parts are both integers. Since the Gaussian integers are closed under addition and multipli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Springer-Verlag
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second-largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business internationally, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
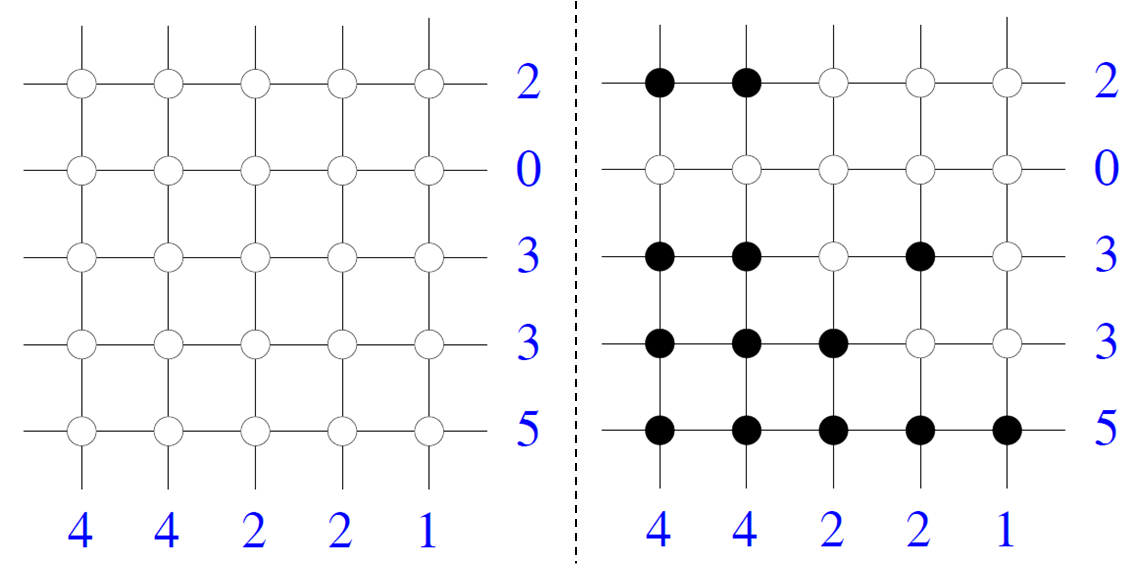
Discrete Tomography
Discrete tomographyHerman, G. T. and Kuba, A., Discrete Tomography: Foundations, Algorithms, and Applications, Birkhäuser Boston, 1999 Herman, G. T. and Kuba, A., Advances in Discrete Tomography and Its Applications, Birkhäuser Boston, 2007 focuses on the problem of reconstruction of binary images (or finite subsets of the integer lattice) from a small number of their projections. In general, tomography deals with the problem of determining shape and dimensional information of an object from a set of projections. From the mathematical point of view, the object corresponds to a function and the problem posed is to reconstruct this function from its integrals or sums over subsets of its domain. In general, the tomographic inversion problem may be continuous or discrete. In continuous tomography both the domain and the range of the function are continuous and line integrals are used. In discrete tomography the domain of the function may be either discrete or continuous, and the ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sums Of Powers
In mathematics and statistics, sums of powers occur in a number of contexts: * Sums of squares arise in many contexts. For example, in geometry, the Pythagorean theorem involves the sum of two squares; in number theory, there are Legendre's three-square theorem and Jacobi's four-square theorem; and in statistics, the analysis of variance involves summing the squares of quantities. *There are only finitely many positive integers that are not sums of ''distinct'' squares. The largest one is 128. The same applies for sums of distinct cubes (largest one is 12,758), distinct fourth powers (largest is 5,134,240), etc. See for a generalization to sums of polynomials. *Faulhaber's formula expresses 1^k + 2^k + 3^k + \cdots + n^k as a polynomial in , or alternatively in terms of a Bernoulli polynomial. *Fermat's right triangle theorem states that there is no solution in positive integers for a^2=b^4+c^4 and a^4=b^4+c^2. *Fermat's Last Theorem states that x^k+y^k=z^k is impossible in posit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Quadruple
A Pythagorean quadruple is a tuple of integers , , , and , such that . They are solutions of a Diophantine equation and often only positive integer values are considered.R. Spira, ''The diophantine equation '', Amer. Math. Monthly Vol. 69 (1962), No. 5, 360–365. However, to provide a more complete geometric interpretation, the integer values can be allowed to be negative and zero (thus allowing Pythagorean triples to be included) with the only condition being that . In this setting, a Pythagorean quadruple defines a cuboid with integer side lengths , , and , whose space diagonal has integer length ; with this interpretation, Pythagorean quadruples are thus also called ''Pythagorean boxes''. In this article we will assume, unless otherwise stated, that the values of a Pythagorean quadruple are all positive integers. Parametrization of primitive quadruples A Pythagorean quadruple is called primitive if the greatest common divisor of its entries is 1. Every Pythagorean quadruple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taxicab Number
In mathematics, the ''n''th taxicab number, typically denoted Ta(''n'') or Taxicab(''n''), is defined as the smallest integer that can be expressed as a sum of two ''positive'' integer cubes in ''n'' distinct ways. The most famous taxicab number is 1729 = Ta(2) = 13 + 123 = 93 + 103, also known as the Hardy–Ramanujan number. The name is derived from a conversation involving mathematicians G. H. Hardy and Srinivasa Ramanujan. As told by Hardy: History and definition The pairs of summands of the Hardy–Ramanujan number Ta(2) = 1729 were first mentioned by Bernard Frénicle de Bessy, who published his observation in 1657. 1729 was made famous as the first taxicab number in the early 20th century by a story involving Srinivasa Ramanujan in claiming it to be the smallest for his particular example of two summands. In 1938, G. H. Hardy and E. M. Wright proved that such numbers exist for all positive integers ''n'', and their proof is easily converted into a program to generat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beal's Conjecture
The Beal conjecture is the following conjecture in number theory: :If :: A^x +B^y = C^z, :where ''A'', ''B'', ''C'', ''x'', ''y'', and ''z'' are positive integers with ''x'', ''y'', ''z'' > 2, then ''A'', ''B'', and ''C'' have a common prime factor. Equivalently, :The equation A^x + B^y = C^z has no solutions in positive integers and pairwise coprime integers ''A, B, C'' if ''x, y, z'' > 2. The conjecture was formulated in 1993 by Andrew Beal, a banker and amateur mathematician, while investigating generalizations of Fermat's Last Theorem. Since 1997, Beal has offered a monetary prize for a peer-reviewed proof of this conjecture or a counterexample. The value of the prize has increased several times and is currently $1 million. In some publications, this conjecture has occasionally been referred to as a generalized Fermat equation, the Mauldin conjecture, and the Tijdeman-Zagier conjecture. Related examples To illustrate, the solution 3^3 + 6^3 = 3^5 has bases with a commo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler's Sum Of Powers Conjecture
In number theory, Euler's conjecture is a disproved conjecture related to Fermat's Last Theorem. It was proposed by Leonhard Euler in 1769. It states that for all integers and greater than 1, if the sum of many th powers of positive integers is itself a th power, then is greater than or equal to : a_1^k + a_2^k + \dots + a_n^k = b^k \implies n \ge k The conjecture represents an attempt to generalize Fermat's Last Theorem, which is the special case : if a_1^k + a_2^k = b^k, then . Although the conjecture holds for the case (which follows from Fermat's Last Theorem for the third powers), it was disproved for and . It is unknown whether the conjecture fails or holds for any value . Background Euler was aware of the equality involving sums of four fourth powers; this, however, is not a counterexample because no term is isolated on one side of the equation. He also provided a complete solution to the four cubes problem as in Plato's number or the taxicab number 1729. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Tomography
Discrete tomographyHerman, G. T. and Kuba, A., Discrete Tomography: Foundations, Algorithms, and Applications, Birkhäuser Boston, 1999 Herman, G. T. and Kuba, A., Advances in Discrete Tomography and Its Applications, Birkhäuser Boston, 2007 focuses on the problem of reconstruction of binary images (or finite subsets of the integer lattice) from a small number of their projections. In general, tomography deals with the problem of determining shape and dimensional information of an object from a set of projections. From the mathematical point of view, the object corresponds to a function and the problem posed is to reconstruct this function from its integrals or sums over subsets of its domain. In general, the tomographic inversion problem may be continuous or discrete. In continuous tomography both the domain and the range of the function are continuous and line integrals are used. In discrete tomography the domain of the function may be either discrete or continuous, and the ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |