Prabhakar Function

	Prabhakar Function Prabhakar function is a certain special function in mathematics introduced by the Indian mathematician Tilak Raj Prabhakar in a paper published in 1971. The function is a three-parameter generalization of the well known two-parameter Mittag-Leffler function in mathematics. The function was originally introduced to solve certain classes of integral equations. Later the function was found to have applications in the theory of fractional calculus and also in certain areas of physics. Definition The one-parameter and two-parameter Mittag-Leffler functions are defined first. Then the definition of the three-parameter Mittag-Leffler function, the Prabhakar function, is presented. In the following definitions, \Gamma (z) is the well known gamma function defined by ::\Gamma(z)= \int_0^\infty t^e^\, dz, \quad\Re(z) > 0. In the following it will be assumed that \alpha, \beta and \gamma are all complex numbers. One-parameter Mittag-Leffler function The one-parameter Mittag-Leffler func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Special Function Special functions are particular mathematical functions that have more or less established names and notations due to their importance in mathematical analysis, functional analysis, geometry, physics, or other applications. The term is defined by consensus, and thus lacks a general formal definition, but the list of mathematical functions contains functions that are commonly accepted as special. Tables of special functions Many special functions appear as solutions of differential equations or integrals of elementary functions. Therefore, tables of integrals usually include descriptions of special functions, and tables of special functions include most important integrals; at least, the integral representation of special functions. Because symmetries of differential equations are essential to both physics and mathematics, the theory of special functions is closely related to the theory of Lie groups and Lie algebras, as well as certain topics in mathematical physics. Symbolic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Tilak Raj Prabhakar Tilak Raj Prabhakar was an Indian mathematician specializing in special functions and integral equations. In a paper published in 1971, he introduced a three-parameter extension of the Mittag-Leffler function. Subsequently, this function was to found to have numerous applications in various areas of mathematics like fractional calculus and also in certain areas of physics. The function has since been named "Prabhakar function" in honor of the person who had introduced it. Education Prabhakar secured his M.A. and B.A. degrees from the Benaras Hindu University (India) and obtained his Ph.D. from the University of Delhi (India) in 1970 with a thesis on "Integral Equations and Special Functions". Career Initially he taught at the S.D. College in Muzzaffarnagar. Then he joined the Multani Mal Modi College in Modinagar where he became Head of the Department of Mathematics and later he moved to the Ramjas College of the University of Delhi. His was an untimely demise. He was profess ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
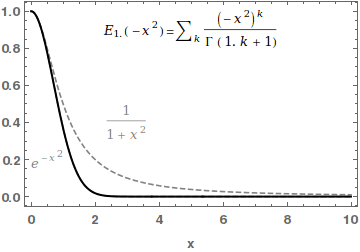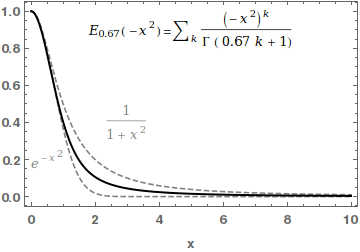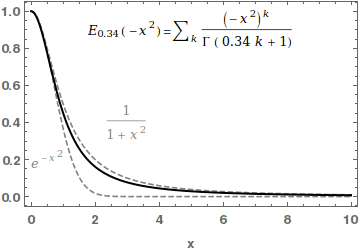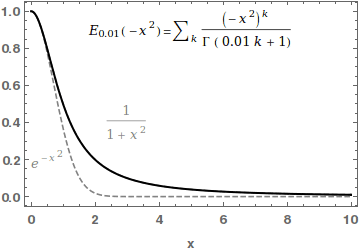
picture info	Mittag-Leffler Function In mathematics, the Mittag-Leffler functions are a family of special functions. They are complex-valued functions of a complex argument ''z'', and moreover depend on one or two complex parameters. The one-parameter Mittag-Leffler function, introduced by Gösta Mittag-Leffler in 1903,Haubold,H J and Mathai,A M and Saxena,R KJ Appl Math 2011, 298628/ref> can be defined by the Maclaurin series :E_ (z) = \sum_^\infty \frac, where \Gamma(x) is the gamma function, and \alpha is a complex parameter with \operatorname\left(\alpha \right)> 0. The two-parameter Mittag-Leffler function, introduced by Wiman in 1905, is occasionally called the generalized Mittag-Leffler function. It has an additional complex parameter \beta, and may be defined by the series :E_ (z) = \sum_^\infty \frac, When \beta=1, the one-parameter function E_\alpha = E_ is recovered. In the case \alpha and \beta are real and positive, the series converges for all values of the argument z, so the Mittag-Leffler fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]