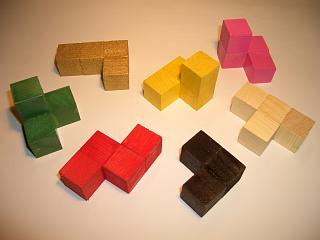|
Polycube
image:tetracube_categories.svg, upAll 8 one-sided tetracubes – if chirality is ignored, the bottom 2 in grey are considered the same, giving 7 free tetracubes in total image:9L cube puzzle solution.svg, A puzzle involving arranging nine L tricubes into a 3×3×3 cube A polycube is a solid figure formed by joining one or more equal cube (geometry), cubes face to face. Polycubes are the three-dimensional analogues of the planar polyominoes. The Soma cube, the Bedlam cube, the Diabolical cube, the Slothouber–Graatsma puzzle, and the Conway puzzle are examples of packing problems based on polycubes. Enumerating polycubes image:AGK-pentacube.png, A Chirality (mathematics), chiral pentacube Like polyominoes, polycubes can be enumerated in two ways, depending on whether Chirality (mathematics), chiral pairs of polycubes (those equivalent by Reflection symmetry, mirror reflection, but not by using only translations and rotations) are counted as one polycube or two. For example, 6 t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diabolical Cube
The diabolical cube is a three-dimensional dissection puzzle consisting of six polycubes (shapes formed by gluing cubes together face to face) that can be assembled together to form a single 3 × 3 × 3 cube.. The six pieces are: one dicube, one tricube, one tetracube, one pentacube, one hexacube and one heptacube, that is, polycubes of 2, 3, 4, 5, 6 and 7 cubes. There are many similar variations of this type of puzzle, including the Soma cube The Soma cube is a mechanical puzzle#Assembly, solid dissection puzzle invented by Danish polymath Piet Hein (scientist), Piet Hein in 1933 during a lecture on quantum mechanics conducted by Werner Heisenberg. Seven different Polycube, pieces ... and the Slothouber–Graatsma puzzle, two other dissections of a 3 × 3 × 3 cube into polycubes which use seven and nine pieces respectively. However, writes that the diabolical cube appears to be the oldest puzzle of this type, first appearing in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube (geometry)
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It is a type of parallelepiped, with pairs of parallel opposite faces, and more specifically a rhombohedron, with congruent edges, and a rectangular cuboid, with right angles between pairs of intersecting faces and pairs of intersecting edges. It is an example of many classes of polyhedra: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron. The cube can be represented in many ways, one of which is the graph known as the cubical graph. It can be constructed by using the Cartesian product of graphs. The cube is the three-dimensional hypercube, a family of polytopes also including the two-dimensional square and four-dimensional tesseract. A cube with 1, unit s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyomino
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling. Polyominoes have been used in popular puzzles since at least 1907, and the enumeration of pentominoes is dated to antiquity. Many results with the pieces of 1 to 6 squares were first published in '' Fairy Chess Review'' between the years 1937 and 1957, under the name of "dissection problems." The name ''polyomino'' was invented by Solomon W. Golomb in 1953, and it was popularized by Martin Gardner in a November 1960 " Mathematical Games" column in ''Scientific American''. Related to polyominoes are polyiamonds, formed from equilateral triangles; polyhexes, formed from regular hexagons; and other plane polyforms. Polyominoes have been generalized to higher dimensions by joining cubes to form polycubes, or hypercubes to form polyhypercubes. In statistical physics, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soma Cube
The Soma cube is a mechanical puzzle#Assembly, solid dissection puzzle invented by Danish polymath Piet Hein (scientist), Piet Hein in 1933 during a lecture on quantum mechanics conducted by Werner Heisenberg. Seven different Polycube, pieces made out of unit cubes must be assembled into a 3×3×3 cube. The pieces can also be used to make a variety of other Three-dimensional space, 3D shapes. The pieces of the Soma cube consist of all possible combinations of at most four unit cubes, joined at their faces, such that at least one inside corner is formed. There are no combinations of one or two cubes that satisfy this condition, but one combination of three cubes and six combinations of four cubes that do. Thus, 3 + (6 × 4) is 27, which is exactly the number of cells in a 3×3×3 cube. Of these seven combinations, two are mirror images of each other (see Chirality (mathematics), Chirality). The Soma cube was popularized by Martin Gardner in the September 1958 Mathematical Games ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bedlam Cube
The Bedlam cube is a solid dissection puzzle invented by British puzzle expert Bruce Bedlam. Design The puzzle consists of thirteen polycubic pieces: twelve pentacubes and one tetracube. The objective is to assemble these pieces into a 4 x 4 x 4 cube. There are 19,186 distinct ways of doing so, up to rotations and reflections. The Bedlam cube is one unit per side larger than the 3 x 3 x 3 Soma cube, and is much more difficult to solve. History Two of the BBC's 'Dragons' from '' Dragons' Den'', Rachel Elnaugh and Theo Paphitis, were to invest in the Bedlam cube during the 2005 series. They offered £100,000 for a 30% share of equity in Bedlam Puzzles. Danny Bamping (the entrepreneur behind Bedlam cube) finally chose a bank loan instead of their investment, as seen in the relevant "Where Are They Now" episode of ''Dragons' Den''. Records According to ''Guinness World Records'', the uncontested world record for assembling the Bedlam Cube is 11.03 seconds by Danny Bam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Slothouber–Graatsma Puzzle
The Slothouber–Graatsma puzzle is a packing problem that calls for packing six 1 × 2 × 2 blocks and three 1 × 1 × 1 blocks into a 3 × 3 × 3 box. The solution to this puzzle is unique (up to mirror reflections and rotations). It was named after its inventors Jan Slothouber and William Graatsma. The puzzle is essentially the same if the three 1 × 1 × 1 blocks are left out, so that the task is to pack six 1 × 2 × 2 blocks into a cubic box with volume 27. Solution The solution of the Slothouber–Graatsma puzzle is straightforward when one realizes that the three 1 × 1 × 1 blocks (or the three holes) need to be placed along a body diagonal of the box, as each of the 3 x 3 layers in the various directions needs to contain such a unit block. This follows from parity (mathematics), parity considerations, because the larger blocks can only fill an even number of the 9 cells in each 3 x 3 layer.Elwyn R. Berlekamp, John H. Conway and Richard K. Guy: Winning ways for your math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentomino
A pentomino (or 5-omino) is a polyomino of order 5; that is, a polygon in the Plane (geometry), plane made of 5 equal-sized squares connected edge to edge. The term is derived from the Greek word for '5' and "domino". When rotation symmetry, rotations and reflection symmetry, reflections are not considered to be distinct shapes, there are 12 different ''Free polyomino, free'' pentominoes. When reflections are considered distinct, there are 18 ''One-sided polyomino, one-sided'' pentominoes. When rotations are also considered distinct, there are 63 ''Fixed polyomino, fixed'' pentominoes. Pentomino tiling puzzles and games are popular in recreational mathematics. Usually, video games such as ''Tetris'' imitations and Rampart (game), ''Rampart'' consider mirror reflections to be distinct, and thus use the full set of 18 one-sided pentominoes. (Tetris itself uses 4-square shapes.) Each of the twelve pentominoes satisfies the Conway criterion; hence, every pentomino is capable of tilin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crucifixion (Corpus Hypercubus)
''Crucifixion (Corpus Hypercubus)'' is a 1954 oil-on-canvas painting by Salvador Dalí. A nontraditional, surrealism, surrealist Crucifixion in art, portrayal of the Crucifixion, it depicts Christ on a polyhedron net of a tesseract (hypercube). It is one of his best-known paintings from the later period of his career. Background During the 1940s and 1950s Dalí's interest in traditional surrealism diminished and he became fascinated with nuclear science, feeling that "thenceforth, the atom was [his] favorite food for thought". The Atomic bombings of Hiroshima and Nagasaki, atomic bombing at the end of World War II left a lasting impression; his 1951 essay "Mystical Manifesto" introduced an art theory he called "nuclear mysticism" that combined his interests in Catholicism, mathematics, science, and Catalonia, Catalan culture in an effort to reestablish classical values and techniques, which he extensively utilized in ''Corpus Hypercubus''. That same year, to promote nuclear myst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two-barred Cross
A two-barred cross is similar to a Latin cross but with an extra bar added. The lengths and placement of the bars (or "arms") vary, and most of the variations are interchangeably called the cross of Lorraine, the patriarchal cross, the Orthodox cross or the archiepiscopal cross. The two bars The two bars can be placed tight together (condensed) or far apart. They can be symmetrically spaced either around the middle, or above or below the middle. One asymmetrical variation has one bar near the top and the other just below the middle. Finally the bars can be of equal length, or with one shorter than the other. Decorations The ends of the arms can be decorated according to different styles. A style with round or rounded ends is called treflée or botonée (from French bouton) in heraldic use. The same style is called budded, apostles' or cathedral cross in religious use. A straight and pointy style called pattée also includes maltese cross variations, and finally a pointed sty ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Salvador Dalí
Salvador Domingo Felipe Jacinto Dalí i Domènech, Marquess of Dalí of Púbol (11 May 190423 January 1989), known as Salvador Dalí ( ; ; ), was a Spanish Surrealism, surrealist artist renowned for his technical skill, precise draftsmanship, and the striking and bizarre images in his work. Born in Figueres in Catalonia, Dalí received his formal education in fine arts in Madrid. Influenced by Impressionism and the Renaissance art, Renaissance masters from a young age, he became increasingly attracted to Cubism and avant-garde movements. He moved closer to Surrealism in the late 1920s and joined the Surrealist group in 1929, soon becoming one of its leading exponents. His best-known work, ''The Persistence of Memory'', was completed in August 1931. Dalí lived in France throughout the Spanish Civil War (1936 to 1939) before leaving for the United States in 1940 where he achieved commercial success. He returned to Spain in 1948 where he announced his return to the Catholic fai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |